The LOGISTIC Procedure
- Overview
- Getting Started
-
Syntax
 PROC LOGISTIC StatementBY StatementCLASS StatementCODE StatementCONTRAST StatementEFFECT StatementEFFECTPLOT StatementESTIMATE StatementEXACT StatementEXACTOPTIONS StatementFREQ StatementID StatementLSMEANS StatementLSMESTIMATE StatementMODEL StatementNLOPTIONS StatementODDSRATIO StatementOUTPUT StatementROC StatementROCCONTRAST StatementSCORE StatementSLICE StatementSTORE StatementSTRATA StatementTEST StatementUNITS StatementWEIGHT Statement
PROC LOGISTIC StatementBY StatementCLASS StatementCODE StatementCONTRAST StatementEFFECT StatementEFFECTPLOT StatementESTIMATE StatementEXACT StatementEXACTOPTIONS StatementFREQ StatementID StatementLSMEANS StatementLSMESTIMATE StatementMODEL StatementNLOPTIONS StatementODDSRATIO StatementOUTPUT StatementROC StatementROCCONTRAST StatementSCORE StatementSLICE StatementSTORE StatementSTRATA StatementTEST StatementUNITS StatementWEIGHT Statement -
Details
 Missing ValuesResponse Level OrderingLink Functions and the Corresponding DistributionsDetermining Observations for Likelihood ContributionsIterative Algorithms for Model FittingConvergence CriteriaExistence of Maximum Likelihood EstimatesEffect-Selection MethodsModel Fitting InformationGeneralized Coefficient of DeterminationScore Statistics and TestsConfidence Intervals for ParametersOdds Ratio EstimationRank Correlation of Observed Responses and Predicted ProbabilitiesLinear Predictor, Predicted Probability, and Confidence LimitsClassification TableOverdispersionThe Hosmer-Lemeshow Goodness-of-Fit TestReceiver Operating Characteristic CurvesTesting Linear Hypotheses about the Regression CoefficientsJoint Tests and Type 3 TestsRegression DiagnosticsScoring Data SetsConditional Logistic RegressionExact Conditional Logistic RegressionInput and Output Data SetsComputational ResourcesDisplayed OutputODS Table NamesODS Graphics
Missing ValuesResponse Level OrderingLink Functions and the Corresponding DistributionsDetermining Observations for Likelihood ContributionsIterative Algorithms for Model FittingConvergence CriteriaExistence of Maximum Likelihood EstimatesEffect-Selection MethodsModel Fitting InformationGeneralized Coefficient of DeterminationScore Statistics and TestsConfidence Intervals for ParametersOdds Ratio EstimationRank Correlation of Observed Responses and Predicted ProbabilitiesLinear Predictor, Predicted Probability, and Confidence LimitsClassification TableOverdispersionThe Hosmer-Lemeshow Goodness-of-Fit TestReceiver Operating Characteristic CurvesTesting Linear Hypotheses about the Regression CoefficientsJoint Tests and Type 3 TestsRegression DiagnosticsScoring Data SetsConditional Logistic RegressionExact Conditional Logistic RegressionInput and Output Data SetsComputational ResourcesDisplayed OutputODS Table NamesODS Graphics -
Examples
 Stepwise Logistic Regression and Predicted ValuesLogistic Modeling with Categorical PredictorsOrdinal Logistic RegressionNominal Response Data: Generalized Logits ModelStratified SamplingLogistic Regression DiagnosticsROC Curve, Customized Odds Ratios, Goodness-of-Fit Statistics, R-Square, and Confidence LimitsComparing Receiver Operating Characteristic CurvesGoodness-of-Fit Tests and SubpopulationsOverdispersionConditional Logistic Regression for Matched Pairs DataExact Conditional Logistic RegressionFirth’s Penalized Likelihood Compared with Other ApproachesComplementary Log-Log Model for Infection RatesComplementary Log-Log Model for Interval-Censored Survival TimesScoring Data SetsUsing the LSMEANS StatementPartial Proportional Odds Model
Stepwise Logistic Regression and Predicted ValuesLogistic Modeling with Categorical PredictorsOrdinal Logistic RegressionNominal Response Data: Generalized Logits ModelStratified SamplingLogistic Regression DiagnosticsROC Curve, Customized Odds Ratios, Goodness-of-Fit Statistics, R-Square, and Confidence LimitsComparing Receiver Operating Characteristic CurvesGoodness-of-Fit Tests and SubpopulationsOverdispersionConditional Logistic Regression for Matched Pairs DataExact Conditional Logistic RegressionFirth’s Penalized Likelihood Compared with Other ApproachesComplementary Log-Log Model for Infection RatesComplementary Log-Log Model for Interval-Censored Survival TimesScoring Data SetsUsing the LSMEANS StatementPartial Proportional Odds Model - References
Example 72.10 Overdispersion
In a seed germination test, seeds of two cultivars were planted in pots of two soil conditions. The following statements create
the data set seeds, which contains the observed proportion of seeds that germinated for various combinations of cultivar and soil condition.
The variable n represents the number of seeds planted in a pot, and the variable r represents the number germinated. The indicator variables cult and soil represent the cultivar and soil condition, respectively.
data seeds; input pot n r cult soil; datalines; 1 16 8 0 0 2 51 26 0 0 3 45 23 0 0 4 39 10 0 0 5 36 9 0 0 6 81 23 1 0 7 30 10 1 0 8 39 17 1 0 9 28 8 1 0 10 62 23 1 0 11 51 32 0 1 12 72 55 0 1 13 41 22 0 1 14 12 3 0 1 15 13 10 0 1 16 79 46 1 1 17 30 15 1 1 18 51 32 1 1 19 74 53 1 1 20 56 12 1 1 ;
PROC LOGISTIC is used as follows to fit a logit model to the data, with cult, soil, and cult 
soil interaction as explanatory variables. The option SCALE=NONE
is specified to display goodness-of-fit statistics.
proc logistic data=seeds; model r/n=cult soil cult*soil/scale=none; title 'Full Model With SCALE=NONE'; run;
Results of fitting the full factorial model are shown in Output 72.10.1. Both Pearson 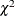 and deviance are highly significant (
and deviance are highly significant (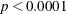 ), suggesting that the model does not fit well.
), suggesting that the model does not fit well.
Output 72.10.1: Results of the Model Fit for the Two-Way Layout
If the link function and the model specification are correct and if there are no outliers, then the lack of fit might be due
to overdispersion. Without adjusting for the overdispersion, the standard errors are likely to be underestimated, causing
the Wald tests to be too sensitive. In PROC LOGISTIC, there are three SCALE=
options to accommodate overdispersion. With unequal sample sizes for the observations, SCALE=
WILLIAMS is preferred. The Williams model estimates a scale parameter  by equating the value of Pearson
by equating the value of Pearson 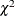 for the full model to its approximate expected value. The full model considered in the following statements is the model
with cultivar, soil condition, and their interaction. Using a full model reduces the risk of contaminating
for the full model to its approximate expected value. The full model considered in the following statements is the model
with cultivar, soil condition, and their interaction. Using a full model reduces the risk of contaminating  with lack of fit due to incorrect model specification.
with lack of fit due to incorrect model specification.
proc logistic data=seeds; model r/n=cult soil cult*soil / scale=williams; title 'Full Model With SCALE=WILLIAMS'; run;
Results of using Williams’ method are shown in Output 72.10.2. The estimate of  is 0.075941 and is given in the formula for the Weight Variable at the beginning of the displayed output.
is 0.075941 and is given in the formula for the Weight Variable at the beginning of the displayed output.
Output 72.10.2: Williams’ Model for Overdispersion
| Deviance and Pearson Goodness-of-Fit Statistics | ||||
|---|---|---|---|---|
| Criterion | Value | DF | Value/DF | Pr > ChiSq |
| Deviance | 16.4402 | 16 | 1.0275 | 0.4227 |
| Pearson | 16.0000 | 16 | 1.0000 | 0.4530 |
| Number of events/trials observations: 20 | |
| Note: | Since the Williams method was used to accommodate overdispersion, the Pearson chi-squared statistic and the deviance can no longer be used to assess the goodness of fit of the model. |
Because neither cult nor cult 
soil is statistically significant (p = 0.5290 and p = 0.9274, respectively), a reduced model that contains only the soil condition factor is fitted, with the observations weighted
by 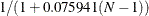 . This can be done conveniently in PROC LOGISTIC by including the scale estimate in the SCALE=WILLIAMS option as follows:
. This can be done conveniently in PROC LOGISTIC by including the scale estimate in the SCALE=WILLIAMS option as follows:
proc logistic data=seeds; model r/n=soil / scale=williams(0.075941); title 'Reduced Model With SCALE=WILLIAMS(0.075941)'; run;
Results of the reduced model fit are shown in Output 72.10.3. Soil condition remains a significant factor (p = 0.0064) for the seed germination.
Output 72.10.3: Reduced Model with Overdispersion Controlled