The LOGISTIC Procedure
- Overview
- Getting Started
-
Syntax
 PROC LOGISTIC StatementBY StatementCLASS StatementCODE StatementCONTRAST StatementEFFECT StatementEFFECTPLOT StatementESTIMATE StatementEXACT StatementEXACTOPTIONS StatementFREQ StatementID StatementLSMEANS StatementLSMESTIMATE StatementMODEL StatementNLOPTIONS StatementODDSRATIO StatementOUTPUT StatementROC StatementROCCONTRAST StatementSCORE StatementSLICE StatementSTORE StatementSTRATA StatementTEST StatementUNITS StatementWEIGHT Statement
PROC LOGISTIC StatementBY StatementCLASS StatementCODE StatementCONTRAST StatementEFFECT StatementEFFECTPLOT StatementESTIMATE StatementEXACT StatementEXACTOPTIONS StatementFREQ StatementID StatementLSMEANS StatementLSMESTIMATE StatementMODEL StatementNLOPTIONS StatementODDSRATIO StatementOUTPUT StatementROC StatementROCCONTRAST StatementSCORE StatementSLICE StatementSTORE StatementSTRATA StatementTEST StatementUNITS StatementWEIGHT Statement -
Details
 Missing ValuesResponse Level OrderingLink Functions and the Corresponding DistributionsDetermining Observations for Likelihood ContributionsIterative Algorithms for Model FittingConvergence CriteriaExistence of Maximum Likelihood EstimatesEffect-Selection MethodsModel Fitting InformationGeneralized Coefficient of DeterminationScore Statistics and TestsConfidence Intervals for ParametersOdds Ratio EstimationRank Correlation of Observed Responses and Predicted ProbabilitiesLinear Predictor, Predicted Probability, and Confidence LimitsClassification TableOverdispersionThe Hosmer-Lemeshow Goodness-of-Fit TestReceiver Operating Characteristic CurvesTesting Linear Hypotheses about the Regression CoefficientsJoint Tests and Type 3 TestsRegression DiagnosticsScoring Data SetsConditional Logistic RegressionExact Conditional Logistic RegressionInput and Output Data SetsComputational ResourcesDisplayed OutputODS Table NamesODS Graphics
Missing ValuesResponse Level OrderingLink Functions and the Corresponding DistributionsDetermining Observations for Likelihood ContributionsIterative Algorithms for Model FittingConvergence CriteriaExistence of Maximum Likelihood EstimatesEffect-Selection MethodsModel Fitting InformationGeneralized Coefficient of DeterminationScore Statistics and TestsConfidence Intervals for ParametersOdds Ratio EstimationRank Correlation of Observed Responses and Predicted ProbabilitiesLinear Predictor, Predicted Probability, and Confidence LimitsClassification TableOverdispersionThe Hosmer-Lemeshow Goodness-of-Fit TestReceiver Operating Characteristic CurvesTesting Linear Hypotheses about the Regression CoefficientsJoint Tests and Type 3 TestsRegression DiagnosticsScoring Data SetsConditional Logistic RegressionExact Conditional Logistic RegressionInput and Output Data SetsComputational ResourcesDisplayed OutputODS Table NamesODS Graphics -
Examples
 Stepwise Logistic Regression and Predicted ValuesLogistic Modeling with Categorical PredictorsOrdinal Logistic RegressionNominal Response Data: Generalized Logits ModelStratified SamplingLogistic Regression DiagnosticsROC Curve, Customized Odds Ratios, Goodness-of-Fit Statistics, R-Square, and Confidence LimitsComparing Receiver Operating Characteristic CurvesGoodness-of-Fit Tests and SubpopulationsOverdispersionConditional Logistic Regression for Matched Pairs DataExact Conditional Logistic RegressionFirth’s Penalized Likelihood Compared with Other ApproachesComplementary Log-Log Model for Infection RatesComplementary Log-Log Model for Interval-Censored Survival TimesScoring Data SetsUsing the LSMEANS StatementPartial Proportional Odds Model
Stepwise Logistic Regression and Predicted ValuesLogistic Modeling with Categorical PredictorsOrdinal Logistic RegressionNominal Response Data: Generalized Logits ModelStratified SamplingLogistic Regression DiagnosticsROC Curve, Customized Odds Ratios, Goodness-of-Fit Statistics, R-Square, and Confidence LimitsComparing Receiver Operating Characteristic CurvesGoodness-of-Fit Tests and SubpopulationsOverdispersionConditional Logistic Regression for Matched Pairs DataExact Conditional Logistic RegressionFirth’s Penalized Likelihood Compared with Other ApproachesComplementary Log-Log Model for Infection RatesComplementary Log-Log Model for Interval-Censored Survival TimesScoring Data SetsUsing the LSMEANS StatementPartial Proportional Odds Model - References
Example 72.18 Partial Proportional Odds Model
Cameron and Trivedi (1998, p. 68) studied the number of doctor visits from the Australian Health Survey 1977–78. The data set contains a dependent
variable, dvisits, which contains the number of doctor visits in the past two weeks (0, 1, or 2, where 2 represents two or more visits) and
the following explanatory variables: sex, which indicates whether the patient is female; age, which contains the patient’s age in years divided by 100; income, which contains the patient’s annual income (in units of $10,000); levyplus, which indicates whether the patient has private health insurance; freepoor, which indicates that the patient has free government health insurance due to low income; freerepa, which indicates that the patient has free government health insurance for other reasons; illness, which contains the number of illnesses in the past two weeks; actdays, which contains the number of days the illness caused reduced activity; hscore, which is a questionnaire score; chcond1, which indicates a chronic condition that does not limit activity; and chcond2, which indicates a chronic condition that limits activity.
data docvisit;
input sex age agesq income levyplus freepoor freerepa
illness actdays hscore chcond1 chcond2 dvisits;
if ( dvisits > 2) then dvisits = 2;
datalines;
1 0.19 0.0361 0.55 1 0 0 1 4 1 0 0 1
1 0.19 0.0361 0.45 1 0 0 1 2 1 0 0 1
0 0.19 0.0361 0.90 0 0 0 3 0 0 0 0 1
... more lines ...
1 0.37 0.1369 0.25 0 0 1 1 0 1 0 0 0
1 0.52 0.2704 0.65 0 0 0 0 0 0 0 0 0
0 0.72 0.5184 0.25 0 0 1 0 0 0 0 0 0
;
Because the response variable dvisits has three levels, the proportional odds model constructs two response functions. There is an intercept parameter for each
of the two response functions, 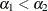 , and common slope parameters
, and common slope parameters 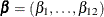 across the functions. The model can be written as
across the functions. The model can be written as
![\[ \mathrm{logit}(\Pr ({Y} \le i~ |~ \mb{x}))= \alpha _{i} + \bbeta ’ \mb{x} , \quad i=1,2 \]](images/statug_logistic0848.png)
The following statements fit a proportional odds model to this data:
proc logistic data=docvisit;
model dvisits = sex age agesq income levyplus
freepoor freerepa illness actdays hscore
chcond1 chcond2;
run;
Selected results are displayed in Output 72.18.1.
Output 72.18.1: Test of Proportional Odds Assumption
The test of the proportional odds assumption in Output 72.18.1 rejects the null hypothesis that all the slopes are equal across the two response functions. This test is very anticonservative; that is, it tends to reject the null hypothesis even when the proportional odds assumption is reasonable.
The proportional odds assumption for ordinal response models can be relaxed by specifying the UNEQUALSLOPES
option in the MODEL statement. A general (nonproportional odds) model has different slope parameters 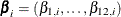 for every logit i:
for every logit i:
![\[ \mathrm{logit}(\Pr ({Y} \le i~ |~ \mb{x}))= \alpha _{i} + \bbeta _{i} ’ \mb{x} , \quad i=1,2 \]](images/statug_logistic0850.png)
The following statements fit the general model:
proc logistic data=docvisit;
model dvisits = sex age agesq income levyplus
freepoor freerepa illness actdays hscore
chcond1 chcond2 / unequalslopes;
sex: test sex_0 =sex_1;
age: test age_0 =age_1;
agesq: test agesq_0 =agesq_1;
income: test income_0 =income_1;
levyplus: test levyplus_0=levyplus_1;
freepoor: test freepoor_0=freepoor_1;
freerepa: test freerepa_0=freerepa_1;
illness: test illness_0 =illness_1;
actdays: test actdays_0 =actdays_1;
hscore: test hscore_0 =hscore_1;
chcond1: test chcond1_0 =chcond1_1;
chcond2: test chcond2_0 =chcond2_1;
run;
The TEST statements test the proportional odds assumption for each of the covariates in the model. The parameter names are constructed by appending the response level that identifies the response function, as described in the section Parameter Names in the OUTEST= Data Set. Selected results from fitting the general model to the data are displayed in Output 72.18.2.
Output 72.18.2: Results for the General Model
| Analysis of Maximum Likelihood Estimates | ||||||
|---|---|---|---|---|---|---|
| Parameter | dvisits | DF | Estimate | Standard Error |
Wald Chi-Square |
Pr > ChiSq |
| Intercept | 0 | 1 | 2.3238 | 0.2754 | 71.2018 | <.0001 |
| Intercept | 1 | 1 | 4.2862 | 0.4890 | 76.8368 | <.0001 |
| sex | 0 | 1 | -0.2637 | 0.0818 | 10.3909 | 0.0013 |
| sex | 1 | 1 | -0.1232 | 0.1451 | 0.7210 | 0.3958 |
| age | 0 | 1 | 1.7489 | 1.5115 | 1.3389 | 0.2472 |
| age | 1 | 1 | -2.0974 | 2.6003 | 0.6506 | 0.4199 |
| agesq | 0 | 1 | -2.4718 | 1.6636 | 2.2076 | 0.1373 |
| agesq | 1 | 1 | 2.6883 | 2.8398 | 0.8961 | 0.3438 |
| income | 0 | 1 | -0.00857 | 0.1266 | 0.0046 | 0.9460 |
| income | 1 | 1 | 0.6464 | 0.2375 | 7.4075 | 0.0065 |
| levyplus | 0 | 1 | -0.2658 | 0.0997 | 7.0999 | 0.0077 |
| levyplus | 1 | 1 | -0.2869 | 0.1820 | 2.4848 | 0.1150 |
| freepoor | 0 | 1 | 0.6773 | 0.2601 | 6.7811 | 0.0092 |
| freepoor | 1 | 1 | 0.9020 | 0.4911 | 3.3730 | 0.0663 |
| freerepa | 0 | 1 | -0.4044 | 0.1382 | 8.5637 | 0.0034 |
| freerepa | 1 | 1 | -0.0958 | 0.2361 | 0.1648 | 0.6848 |
| illness | 0 | 1 | -0.2645 | 0.0287 | 84.6792 | <.0001 |
| illness | 1 | 1 | -0.3083 | 0.0499 | 38.1652 | <.0001 |
| actdays | 0 | 1 | -0.1521 | 0.0116 | 172.2764 | <.0001 |
| actdays | 1 | 1 | -0.1863 | 0.0134 | 193.7700 | <.0001 |
| hscore | 0 | 1 | -0.0620 | 0.0172 | 12.9996 | 0.0003 |
| hscore | 1 | 1 | -0.0568 | 0.0252 | 5.0940 | 0.0240 |
| chcond1 | 0 | 1 | -0.1140 | 0.0909 | 1.5721 | 0.2099 |
| chcond1 | 1 | 1 | -0.2478 | 0.1743 | 2.0201 | 0.1552 |
| chcond2 | 0 | 1 | -0.2660 | 0.1255 | 4.4918 | 0.0341 |
| chcond2 | 1 | 1 | -0.3146 | 0.2116 | 2.2106 | 0.1371 |
| Linear Hypotheses Testing Results | |||
|---|---|---|---|
| Label | Wald Chi-Square |
DF | Pr > ChiSq |
| sex | 1.0981 | 1 | 0.2947 |
| age | 2.5658 | 1 | 0.1092 |
| agesq | 3.8309 | 1 | 0.0503 |
| income | 8.8006 | 1 | 0.0030 |
| levyplus | 0.0162 | 1 | 0.8989 |
| freepoor | 0.2569 | 1 | 0.6122 |
| freerepa | 2.0099 | 1 | 0.1563 |
| illness | 0.8630 | 1 | 0.3529 |
| actdays | 6.9407 | 1 | 0.0084 |
| hscore | 0.0476 | 1 | 0.8273 |
| chcond1 | 0.6906 | 1 | 0.4060 |
| chcond2 | 0.0615 | 1 | 0.8042 |
The preceding general model fits 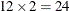 slope parameters, and according to the "Linear Hypotheses Testing Results" table in Output 72.18.2, several variables are unnecessarily allowing nonproportional odds. You can obtain a more parsimonious model by specifying
a subset of the parameters to have nonproportional odds. The following statements allow the parameters for the variables in
the "Linear Hypotheses Testing Results" table that have p-values less than 0.1 (
slope parameters, and according to the "Linear Hypotheses Testing Results" table in Output 72.18.2, several variables are unnecessarily allowing nonproportional odds. You can obtain a more parsimonious model by specifying
a subset of the parameters to have nonproportional odds. The following statements allow the parameters for the variables in
the "Linear Hypotheses Testing Results" table that have p-values less than 0.1 (actdays, agesq, and income) to vary across the response functions:
proc logistic data=docvisit;
model dvisits= sex age agesq income levyplus freepoor
freerepa illness actdays hscore chcond1 chcond2
/ unequalslopes=(actdays agesq income);
run;
Selected results from fitting this partial proportional odds model are displayed in Output 72.18.3.
Output 72.18.3: Results for Partial Proportional Odds Model
| Analysis of Maximum Likelihood Estimates | ||||||
|---|---|---|---|---|---|---|
| Parameter | dvisits | DF | Estimate | Standard Error |
Wald Chi-Square |
Pr > ChiSq |
| Intercept | 0 | 1 | 2.3882 | 0.2716 | 77.2988 | <.0001 |
| Intercept | 1 | 1 | 3.7597 | 0.3138 | 143.5386 | <.0001 |
| sex | 1 | -0.2485 | 0.0807 | 9.4789 | 0.0021 | |
| age | 1 | 1.3000 | 1.4864 | 0.7649 | 0.3818 | |
| agesq | 0 | 1 | -2.0110 | 1.6345 | 1.5139 | 0.2186 |
| agesq | 1 | 1 | -0.8789 | 1.6512 | 0.2833 | 0.5945 |
| income | 0 | 1 | 0.0209 | 0.1261 | 0.0275 | 0.8683 |
| income | 1 | 1 | 0.4283 | 0.2221 | 3.7190 | 0.0538 |
| levyplus | 1 | -0.2703 | 0.0989 | 7.4735 | 0.0063 | |
| freepoor | 1 | 0.6936 | 0.2589 | 7.1785 | 0.0074 | |
| freerepa | 1 | -0.3648 | 0.1358 | 7.2155 | 0.0072 | |
| illness | 1 | -0.2707 | 0.0281 | 92.7123 | <.0001 | |
| actdays | 0 | 1 | -0.1522 | 0.0115 | 173.5696 | <.0001 |
| actdays | 1 | 1 | -0.1868 | 0.0129 | 209.7134 | <.0001 |
| hscore | 1 | -0.0609 | 0.0166 | 13.5137 | 0.0002 | |
| chcond1 | 1 | -0.1200 | 0.0901 | 1.7756 | 0.1827 | |
| chcond2 | 1 | -0.2628 | 0.1227 | 4.5849 | 0.0323 | |
You can also specify the following code to let stepwise selection determine which parameters have unequal slopes:
proc logistic data=docvisit;
model dvisits= sex age agesq income levyplus freepoor
freerepa illness actdays hscore chcond1 chcond2
/ equalslopes unequalslopes selection=stepwise details;
run;
This selection process chooses sex, freepoor, illness, and hscore as the proportional odds effects and chooses U_actdays and U_agesq as the unconstrained general effects. For more information about model selection for partial proportional odds models, see
Derr (2013).
The partial proportional odds model can be written in the same form as the general model by letting 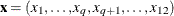 and
and 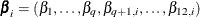 . So the first q parameters have proportional odds and the remaining parameters do not. The last 12 – q parameters can be rewritten to have a common slope plus an increment from the common slope:
. So the first q parameters have proportional odds and the remaining parameters do not. The last 12 – q parameters can be rewritten to have a common slope plus an increment from the common slope: 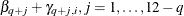 , where the new parameters
, where the new parameters 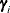 contain the increments from the common slopes. The model in this form makes it obvious that the proportional odds model is
a submodel of the partial proportional odds model, and both of these are submodels of the general model. This means that you
can use likelihood ratio tests to compare models.
contain the increments from the common slopes. The model in this form makes it obvious that the proportional odds model is
a submodel of the partial proportional odds model, and both of these are submodels of the general model. This means that you
can use likelihood ratio tests to compare models.
You can use the following statements to compute the likelihood ratio tests from the Likelihood Ratio row of the "Testing Global Null hypothesis: BETA=0" tables in the preceding outputs:
data a; label p='Pr>ChiSq'; format p 8.6; input Test $10. ChiSq1 DF1 ChiSq2 DF2; ChiSq= ChiSq1-ChiSq2; DF= DF1-DF2; p=1-probchi(ChiSq,DF); keep Test Chisq DF p; datalines; Gen vs PO 761.4797 24 734.2971 12 PPO vs PO 752.5512 15 734.2971 12 Gen vs PPO 761.4797 24 752.5512 15 ; proc print data=a label noobs; var Test ChiSq DF p; run;
Output 72.18.4: Likelihood Ratio Tests
Therefore, you reject the proportional odds model in favor of both the general model and the partial proportional odds model, and the partial proportional odds model fits as well as the general model. The likelihood ratio test of the general model versus the proportional odds model is very similar to the score test of the proportional odds assumption in Output 72.18.1 because of the large sample size (Stokes, Davis, and Koch 2000, p. 249).
Note: The proportional odds model has increasing intercepts, which ensures the increasing nature of the cumulative response functions. However, none of the parameters in the partial proportional odds or general models are constrained. Because of this, sometimes during the optimization process a predicted individual probability can be negative; the optimization continues because it might recover from this situation. Sometimes your final model will predict negative individual probabilities for some of the observations; in this case a message is displayed, and you should check your data for outliers and possibly redefine your model. Other times the model fits your data well, but if you try to score new data you can get negative individual probabilities. This means the model is not appropriate for the data you are trying to score, a message is displayed, and the estimates are set to missing. These optimization issues do not arise when you fit an adjacent-category or generalized logit model that has equal and unequal slope effects.