The LOGISTIC Procedure
- Overview
- Getting Started
-
Syntax
 PROC LOGISTIC StatementBY StatementCLASS StatementCODE StatementCONTRAST StatementEFFECT StatementEFFECTPLOT StatementESTIMATE StatementEXACT StatementEXACTOPTIONS StatementFREQ StatementID StatementLSMEANS StatementLSMESTIMATE StatementMODEL StatementNLOPTIONS StatementODDSRATIO StatementOUTPUT StatementROC StatementROCCONTRAST StatementSCORE StatementSLICE StatementSTORE StatementSTRATA StatementTEST StatementUNITS StatementWEIGHT Statement
PROC LOGISTIC StatementBY StatementCLASS StatementCODE StatementCONTRAST StatementEFFECT StatementEFFECTPLOT StatementESTIMATE StatementEXACT StatementEXACTOPTIONS StatementFREQ StatementID StatementLSMEANS StatementLSMESTIMATE StatementMODEL StatementNLOPTIONS StatementODDSRATIO StatementOUTPUT StatementROC StatementROCCONTRAST StatementSCORE StatementSLICE StatementSTORE StatementSTRATA StatementTEST StatementUNITS StatementWEIGHT Statement -
Details
 Missing ValuesResponse Level OrderingLink Functions and the Corresponding DistributionsDetermining Observations for Likelihood ContributionsIterative Algorithms for Model FittingConvergence CriteriaExistence of Maximum Likelihood EstimatesEffect-Selection MethodsModel Fitting InformationGeneralized Coefficient of DeterminationScore Statistics and TestsConfidence Intervals for ParametersOdds Ratio EstimationRank Correlation of Observed Responses and Predicted ProbabilitiesLinear Predictor, Predicted Probability, and Confidence LimitsClassification TableOverdispersionThe Hosmer-Lemeshow Goodness-of-Fit TestReceiver Operating Characteristic CurvesTesting Linear Hypotheses about the Regression CoefficientsJoint Tests and Type 3 TestsRegression DiagnosticsScoring Data SetsConditional Logistic RegressionExact Conditional Logistic RegressionInput and Output Data SetsComputational ResourcesDisplayed OutputODS Table NamesODS Graphics
Missing ValuesResponse Level OrderingLink Functions and the Corresponding DistributionsDetermining Observations for Likelihood ContributionsIterative Algorithms for Model FittingConvergence CriteriaExistence of Maximum Likelihood EstimatesEffect-Selection MethodsModel Fitting InformationGeneralized Coefficient of DeterminationScore Statistics and TestsConfidence Intervals for ParametersOdds Ratio EstimationRank Correlation of Observed Responses and Predicted ProbabilitiesLinear Predictor, Predicted Probability, and Confidence LimitsClassification TableOverdispersionThe Hosmer-Lemeshow Goodness-of-Fit TestReceiver Operating Characteristic CurvesTesting Linear Hypotheses about the Regression CoefficientsJoint Tests and Type 3 TestsRegression DiagnosticsScoring Data SetsConditional Logistic RegressionExact Conditional Logistic RegressionInput and Output Data SetsComputational ResourcesDisplayed OutputODS Table NamesODS Graphics -
Examples
 Stepwise Logistic Regression and Predicted ValuesLogistic Modeling with Categorical PredictorsOrdinal Logistic RegressionNominal Response Data: Generalized Logits ModelStratified SamplingLogistic Regression DiagnosticsROC Curve, Customized Odds Ratios, Goodness-of-Fit Statistics, R-Square, and Confidence LimitsComparing Receiver Operating Characteristic CurvesGoodness-of-Fit Tests and SubpopulationsOverdispersionConditional Logistic Regression for Matched Pairs DataExact Conditional Logistic RegressionFirth’s Penalized Likelihood Compared with Other ApproachesComplementary Log-Log Model for Infection RatesComplementary Log-Log Model for Interval-Censored Survival TimesScoring Data SetsUsing the LSMEANS StatementPartial Proportional Odds Model
Stepwise Logistic Regression and Predicted ValuesLogistic Modeling with Categorical PredictorsOrdinal Logistic RegressionNominal Response Data: Generalized Logits ModelStratified SamplingLogistic Regression DiagnosticsROC Curve, Customized Odds Ratios, Goodness-of-Fit Statistics, R-Square, and Confidence LimitsComparing Receiver Operating Characteristic CurvesGoodness-of-Fit Tests and SubpopulationsOverdispersionConditional Logistic Regression for Matched Pairs DataExact Conditional Logistic RegressionFirth’s Penalized Likelihood Compared with Other ApproachesComplementary Log-Log Model for Infection RatesComplementary Log-Log Model for Interval-Censored Survival TimesScoring Data SetsUsing the LSMEANS StatementPartial Proportional Odds Model - References
TEST Statement
-
<label:> TEST equation1 <, equation2, …> </ option>;
The TEST statement tests linear hypotheses about the regression coefficients. The Wald test is used to perform a joint test
of the null hypotheses  specified in a single TEST statement, where
specified in a single TEST statement, where 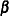 is the vector of intercept and slope parameters. When
is the vector of intercept and slope parameters. When  you should specify a CONTRAST
statement instead.
you should specify a CONTRAST
statement instead.
Each equation specifies a linear hypothesis (a row of the  matrix and the corresponding element of the
matrix and the corresponding element of the  vector). Multiple equations are separated by commas. The label, which must be a valid SAS name, is used to identify the resulting output and should always be included. You can submit multiple
TEST statements.
vector). Multiple equations are separated by commas. The label, which must be a valid SAS name, is used to identify the resulting output and should always be included. You can submit multiple
TEST statements.
The form of an equation is as follows:
term< term
term  > <
> < term <
term < term
term >>
>>
where term is a parameter of the model, or a constant, or a constant times a parameter. Intercept and CLASS variable parameter names should be specified as described in the section Parameter Names in the OUTEST= Data Set. For multinomial response models, this form enables you to construct tests of parameters from specific logits. When no equal sign appears, the expression is set to 0. The following statements illustrate possible uses of the TEST statement:
proc logistic; model y= a1 a2 a3 a4; test1: test intercept + .5 * a2 = 0; test2: test intercept + .5 * a2; test3: test a1=a2=a3; test4: test a1=a2, a2=a3; run;
Note that the first and second TEST statements are equivalent, as are the third and fourth TEST statements.
You can specify the following option in the TEST statement after a slash(/):


![$[{\bL \widehat{\bV }({\widehat{\bbeta }})\bL ’}]^{-1}$](images/statug_logistic0137.png)
![$[{\bL \widehat{\bV }({\widehat{\bbeta }})\bL ’}]^{-1}(\bL {\widehat{\bbeta }} - \mb{c})$](images/statug_logistic0138.png)