The LOGISTIC Procedure
- Overview
- Getting Started
-
Syntax
 PROC LOGISTIC StatementBY StatementCLASS StatementCODE StatementCONTRAST StatementEFFECT StatementEFFECTPLOT StatementESTIMATE StatementEXACT StatementEXACTOPTIONS StatementFREQ StatementID StatementLSMEANS StatementLSMESTIMATE StatementMODEL StatementNLOPTIONS StatementODDSRATIO StatementOUTPUT StatementROC StatementROCCONTRAST StatementSCORE StatementSLICE StatementSTORE StatementSTRATA StatementTEST StatementUNITS StatementWEIGHT Statement
PROC LOGISTIC StatementBY StatementCLASS StatementCODE StatementCONTRAST StatementEFFECT StatementEFFECTPLOT StatementESTIMATE StatementEXACT StatementEXACTOPTIONS StatementFREQ StatementID StatementLSMEANS StatementLSMESTIMATE StatementMODEL StatementNLOPTIONS StatementODDSRATIO StatementOUTPUT StatementROC StatementROCCONTRAST StatementSCORE StatementSLICE StatementSTORE StatementSTRATA StatementTEST StatementUNITS StatementWEIGHT Statement -
Details
 Missing ValuesResponse Level OrderingLink Functions and the Corresponding DistributionsDetermining Observations for Likelihood ContributionsIterative Algorithms for Model FittingConvergence CriteriaExistence of Maximum Likelihood EstimatesEffect-Selection MethodsModel Fitting InformationGeneralized Coefficient of DeterminationScore Statistics and TestsConfidence Intervals for ParametersOdds Ratio EstimationRank Correlation of Observed Responses and Predicted ProbabilitiesLinear Predictor, Predicted Probability, and Confidence LimitsClassification TableOverdispersionThe Hosmer-Lemeshow Goodness-of-Fit TestReceiver Operating Characteristic CurvesTesting Linear Hypotheses about the Regression CoefficientsJoint Tests and Type 3 TestsRegression DiagnosticsScoring Data SetsConditional Logistic RegressionExact Conditional Logistic RegressionInput and Output Data SetsComputational ResourcesDisplayed OutputODS Table NamesODS Graphics
Missing ValuesResponse Level OrderingLink Functions and the Corresponding DistributionsDetermining Observations for Likelihood ContributionsIterative Algorithms for Model FittingConvergence CriteriaExistence of Maximum Likelihood EstimatesEffect-Selection MethodsModel Fitting InformationGeneralized Coefficient of DeterminationScore Statistics and TestsConfidence Intervals for ParametersOdds Ratio EstimationRank Correlation of Observed Responses and Predicted ProbabilitiesLinear Predictor, Predicted Probability, and Confidence LimitsClassification TableOverdispersionThe Hosmer-Lemeshow Goodness-of-Fit TestReceiver Operating Characteristic CurvesTesting Linear Hypotheses about the Regression CoefficientsJoint Tests and Type 3 TestsRegression DiagnosticsScoring Data SetsConditional Logistic RegressionExact Conditional Logistic RegressionInput and Output Data SetsComputational ResourcesDisplayed OutputODS Table NamesODS Graphics -
Examples
 Stepwise Logistic Regression and Predicted ValuesLogistic Modeling with Categorical PredictorsOrdinal Logistic RegressionNominal Response Data: Generalized Logits ModelStratified SamplingLogistic Regression DiagnosticsROC Curve, Customized Odds Ratios, Goodness-of-Fit Statistics, R-Square, and Confidence LimitsComparing Receiver Operating Characteristic CurvesGoodness-of-Fit Tests and SubpopulationsOverdispersionConditional Logistic Regression for Matched Pairs DataExact Conditional Logistic RegressionFirth’s Penalized Likelihood Compared with Other ApproachesComplementary Log-Log Model for Infection RatesComplementary Log-Log Model for Interval-Censored Survival TimesScoring Data SetsUsing the LSMEANS StatementPartial Proportional Odds Model
Stepwise Logistic Regression and Predicted ValuesLogistic Modeling with Categorical PredictorsOrdinal Logistic RegressionNominal Response Data: Generalized Logits ModelStratified SamplingLogistic Regression DiagnosticsROC Curve, Customized Odds Ratios, Goodness-of-Fit Statistics, R-Square, and Confidence LimitsComparing Receiver Operating Characteristic CurvesGoodness-of-Fit Tests and SubpopulationsOverdispersionConditional Logistic Regression for Matched Pairs DataExact Conditional Logistic RegressionFirth’s Penalized Likelihood Compared with Other ApproachesComplementary Log-Log Model for Infection RatesComplementary Log-Log Model for Interval-Censored Survival TimesScoring Data SetsUsing the LSMEANS StatementPartial Proportional Odds Model - References
Example 72.1 Stepwise Logistic Regression and Predicted Values
Consider a study on cancer remission (Lee 1974). The data consist of patient characteristics and whether or not cancer remission occurred. The following DATA step creates
the data set Remission containing seven variables. The variable remiss is the cancer remission indicator variable with a value of 1 for remission and a value of 0 for nonremission. The other six
variables are the risk factors thought to be related to cancer remission.
data Remission; input remiss cell smear infil li blast temp; label remiss='Complete Remission'; datalines; 1 .8 .83 .66 1.9 1.1 .996 1 .9 .36 .32 1.4 .74 .992 0 .8 .88 .7 .8 .176 .982 0 1 .87 .87 .7 1.053 .986 1 .9 .75 .68 1.3 .519 .98 0 1 .65 .65 .6 .519 .982 1 .95 .97 .92 1 1.23 .992 0 .95 .87 .83 1.9 1.354 1.02 0 1 .45 .45 .8 .322 .999 0 .95 .36 .34 .5 0 1.038 0 .85 .39 .33 .7 .279 .988 0 .7 .76 .53 1.2 .146 .982 0 .8 .46 .37 .4 .38 1.006 0 .2 .39 .08 .8 .114 .99 0 1 .9 .9 1.1 1.037 .99 1 1 .84 .84 1.9 2.064 1.02 0 .65 .42 .27 .5 .114 1.014 0 1 .75 .75 1 1.322 1.004 0 .5 .44 .22 .6 .114 .99 1 1 .63 .63 1.1 1.072 .986 0 1 .33 .33 .4 .176 1.01 0 .9 .93 .84 .6 1.591 1.02 1 1 .58 .58 1 .531 1.002 0 .95 .32 .3 1.6 .886 .988 1 1 .6 .6 1.7 .964 .99 1 1 .69 .69 .9 .398 .986 0 1 .73 .73 .7 .398 .986 ;
The following invocation of PROC LOGISTIC illustrates the use of stepwise selection
to identify the prognostic factors for cancer remission. A significance level of 0.3 is required to allow a variable into
the model (SLENTRY=
0.3), and a significance level of 0.35 is required for a variable to stay in the model (SLSTAY=
0.35). A detailed account of the variable selection process is requested by specifying the DETAILS
option. The Hosmer and Lemeshow goodness-of-fit test for the final selected model is requested by specifying the LACKFIT
option. The OUTEST=
and COVOUT
options in the PROC LOGISTIC statement create a data set that contains parameter estimates and their covariances for the
final selected model. The response variable option EVENT=
chooses remiss=1 (remission) as the event so that the probability of remission is modeled. The OUTPUT
statement creates a data set that contains the cumulative predicted probabilities and the corresponding confidence limits,
and the individual and cross validated predicted probabilities for each observation. The ODS OUTPUT statement writes the "Association"
table from each selection step to a SAS data set.
title 'Stepwise Regression on Cancer Remission Data';
proc logistic data=Remission outest=betas covout;
model remiss(event='1')=cell smear infil li blast temp
/ selection=stepwise
slentry=0.3
slstay=0.35
details
lackfit;
output out=pred p=phat lower=lcl upper=ucl
predprob=(individual crossvalidate);
ods output Association=Association;
run;
proc print data=betas; title2 'Parameter Estimates and Covariance Matrix'; run;
proc print data=pred; title2 'Predicted Probabilities and 95% Confidence Limits'; run;
In stepwise selection, an attempt is made to remove any insignificant variables from the model before adding a significant variable to the model. Each addition or deletion of a variable to or from a model is listed as a separate step in the displayed output, and at each step a new model is fitted. Details of the model selection steps are shown in Outputs Output 72.1.1 through Output 72.1.5.
Prior to the first step, the intercept-only model is fit and individual score statistics for the potential variables are evaluated (Output 72.1.1).
Output 72.1.1: Startup Model
In Step 1 (Output 72.1.2), the variable li is selected into the model because it is the most significant variable among those to be chosen (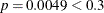 ). The intermediate model that contains an intercept and
). The intermediate model that contains an intercept and li is then fitted. li remains significant (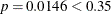 ) and is not removed.
) and is not removed.
Output 72.1.2: Step 1 of the Stepwise Analysis
In Step 2 (Output 72.1.3), the variable temp is added to the model. The model then contains an intercept and the variables li and temp. Both li and temp remain significant at 0.35 level; therefore, neither li nor temp is removed from the model.
Output 72.1.3: Step 2 of the Stepwise Analysis
In Step 3 (Output 72.1.4), the variable cell is added to the model. The model then contains an intercept and the variables li, temp, and cell. None of these variables are removed from the model because all are significant at the 0.35 level.
Output 72.1.4: Step 3 of the Stepwise Analysis
Finally, none of the remaining variables outside the model meet the entry criterion, and the stepwise selection is terminated. A summary of the stepwise selection is displayed in Output 72.1.5.
Output 72.1.5: Summary of the Stepwise Selection
Results of the Hosmer and Lemeshow test are shown in Output 72.1.6. There is no evidence of a lack of fit in the selected model 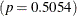 .
.
Output 72.1.6: Display of the LACKFIT Option
The data set betas created by the OUTEST=
and COVOUT
options is displayed in Output 72.1.7. The data set contains parameter estimates and the covariance matrix for the final selected model. Note that all explanatory
variables listed in the MODEL
statement are included in this data set; however, variables that are not included in the final model have all missing values.
Output 72.1.7: Data Set of Estimates and Covariances
| Stepwise Regression on Cancer Remission Data |
| Parameter Estimates and Covariance Matrix |
| Obs | _LINK_ | _TYPE_ | _STATUS_ | _NAME_ | Intercept | cell | smear | infil | li | blast | temp | _LNLIKE_ | _ESTTYPE_ |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | LOGIT | PARMS | 0 Converged | remiss | 67.63 | 9.652 | . | . | 3.8671 | . | -82.07 | -10.9767 | MLE |
| 2 | LOGIT | COV | 0 Converged | Intercept | 3236.19 | 157.097 | . | . | 64.5726 | . | -3483.23 | -10.9767 | MLE |
| 3 | LOGIT | COV | 0 Converged | cell | 157.10 | 60.079 | . | . | 6.9454 | . | -223.67 | -10.9767 | MLE |
| 4 | LOGIT | COV | 0 Converged | smear | . | . | . | . | . | . | . | -10.9767 | MLE |
| 5 | LOGIT | COV | 0 Converged | infil | . | . | . | . | . | . | . | -10.9767 | MLE |
| 6 | LOGIT | COV | 0 Converged | li | 64.57 | 6.945 | . | . | 3.1623 | . | -75.35 | -10.9767 | MLE |
| 7 | LOGIT | COV | 0 Converged | blast | . | . | . | . | . | . | . | -10.9767 | MLE |
| 8 | LOGIT | COV | 0 Converged | temp | -3483.23 | -223.669 | . | . | -75.3513 | . | 3808.42 | -10.9767 | MLE |
The data set pred created by the OUTPUT
statement is displayed in Output 72.1.8. It contains all the variables in the input data set, the variable phat for the (cumulative) predicted probability, the variables lcl and ucl for the lower and upper confidence limits for the probability, and four other variables (IP_1, IP_0, XP_1, and XP_0) for the PREDPROBS=
option. The data set also contains the variable _LEVEL_, indicating the response value to which phat, lcl, and ucl refer. For instance, for the first row of the OUTPUT data set, the values of _LEVEL_ and phat, lcl, and ucl are 1, 0.72265, 0.16892, and 0.97093, respectively; this means that the estimated probability that remiss=1 is 0.723 for the given explanatory variable values, and the corresponding 95% confidence interval is (0.16892, 0.97093).
The variables IP_1 and IP_0 contain the predicted probabilities that remiss=1 and remiss=0, respectively. Note that values of phat and IP_1 are identical because they both contain the probabilities that remiss=1. The variables XP_1 and XP_0 contain the cross validated predicted probabilities that remiss=1 and remiss=0, respectively.
Output 72.1.8: Predicted Probabilities and Confidence Intervals
| Stepwise Regression on Cancer Remission Data |
| Predicted Probabilities and 95% Confidence Limits |
| Obs | remiss | cell | smear | infil | li | blast | temp | _FROM_ | _INTO_ | IP_0 | IP_1 | XP_0 | XP_1 | _LEVEL_ | phat | lcl | ucl |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 0.80 | 0.83 | 0.66 | 1.9 | 1.100 | 0.996 | 1 | 1 | 0.27735 | 0.72265 | 0.43873 | 0.56127 | 1 | 0.72265 | 0.16892 | 0.97093 |
| 2 | 1 | 0.90 | 0.36 | 0.32 | 1.4 | 0.740 | 0.992 | 1 | 1 | 0.42126 | 0.57874 | 0.47461 | 0.52539 | 1 | 0.57874 | 0.26788 | 0.83762 |
| 3 | 0 | 0.80 | 0.88 | 0.70 | 0.8 | 0.176 | 0.982 | 0 | 0 | 0.89540 | 0.10460 | 0.87060 | 0.12940 | 1 | 0.10460 | 0.00781 | 0.63419 |
| 4 | 0 | 1.00 | 0.87 | 0.87 | 0.7 | 1.053 | 0.986 | 0 | 0 | 0.71742 | 0.28258 | 0.67259 | 0.32741 | 1 | 0.28258 | 0.07498 | 0.65683 |
| 5 | 1 | 0.90 | 0.75 | 0.68 | 1.3 | 0.519 | 0.980 | 1 | 1 | 0.28582 | 0.71418 | 0.36901 | 0.63099 | 1 | 0.71418 | 0.25218 | 0.94876 |
| 6 | 0 | 1.00 | 0.65 | 0.65 | 0.6 | 0.519 | 0.982 | 0 | 0 | 0.72911 | 0.27089 | 0.67269 | 0.32731 | 1 | 0.27089 | 0.05852 | 0.68951 |
| 7 | 1 | 0.95 | 0.97 | 0.92 | 1.0 | 1.230 | 0.992 | 1 | 0 | 0.67844 | 0.32156 | 0.72923 | 0.27077 | 1 | 0.32156 | 0.13255 | 0.59516 |
| 8 | 0 | 0.95 | 0.87 | 0.83 | 1.9 | 1.354 | 1.020 | 0 | 1 | 0.39277 | 0.60723 | 0.09906 | 0.90094 | 1 | 0.60723 | 0.10572 | 0.95287 |
| 9 | 0 | 1.00 | 0.45 | 0.45 | 0.8 | 0.322 | 0.999 | 0 | 0 | 0.83368 | 0.16632 | 0.80864 | 0.19136 | 1 | 0.16632 | 0.03018 | 0.56123 |
| 10 | 0 | 0.95 | 0.36 | 0.34 | 0.5 | 0.000 | 1.038 | 0 | 0 | 0.99843 | 0.00157 | 0.99840 | 0.00160 | 1 | 0.00157 | 0.00000 | 0.68962 |
| 11 | 0 | 0.85 | 0.39 | 0.33 | 0.7 | 0.279 | 0.988 | 0 | 0 | 0.92715 | 0.07285 | 0.91723 | 0.08277 | 1 | 0.07285 | 0.00614 | 0.49982 |
| 12 | 0 | 0.70 | 0.76 | 0.53 | 1.2 | 0.146 | 0.982 | 0 | 0 | 0.82714 | 0.17286 | 0.63838 | 0.36162 | 1 | 0.17286 | 0.00637 | 0.87206 |
| 13 | 0 | 0.80 | 0.46 | 0.37 | 0.4 | 0.380 | 1.006 | 0 | 0 | 0.99654 | 0.00346 | 0.99644 | 0.00356 | 1 | 0.00346 | 0.00001 | 0.46530 |
| 14 | 0 | 0.20 | 0.39 | 0.08 | 0.8 | 0.114 | 0.990 | 0 | 0 | 0.99982 | 0.00018 | 0.99981 | 0.00019 | 1 | 0.00018 | 0.00000 | 0.96482 |
| 15 | 0 | 1.00 | 0.90 | 0.90 | 1.1 | 1.037 | 0.990 | 0 | 1 | 0.42878 | 0.57122 | 0.35354 | 0.64646 | 1 | 0.57122 | 0.25303 | 0.83973 |
| 16 | 1 | 1.00 | 0.84 | 0.84 | 1.9 | 2.064 | 1.020 | 1 | 1 | 0.28530 | 0.71470 | 0.47213 | 0.52787 | 1 | 0.71470 | 0.15362 | 0.97189 |
| 17 | 0 | 0.65 | 0.42 | 0.27 | 0.5 | 0.114 | 1.014 | 0 | 0 | 0.99938 | 0.00062 | 0.99937 | 0.00063 | 1 | 0.00062 | 0.00000 | 0.62665 |
| 18 | 0 | 1.00 | 0.75 | 0.75 | 1.0 | 1.322 | 1.004 | 0 | 0 | 0.77711 | 0.22289 | 0.73612 | 0.26388 | 1 | 0.22289 | 0.04483 | 0.63670 |
| 19 | 0 | 0.50 | 0.44 | 0.22 | 0.6 | 0.114 | 0.990 | 0 | 0 | 0.99846 | 0.00154 | 0.99842 | 0.00158 | 1 | 0.00154 | 0.00000 | 0.79644 |
| 20 | 1 | 1.00 | 0.63 | 0.63 | 1.1 | 1.072 | 0.986 | 1 | 1 | 0.35089 | 0.64911 | 0.42053 | 0.57947 | 1 | 0.64911 | 0.26305 | 0.90555 |
| 21 | 0 | 1.00 | 0.33 | 0.33 | 0.4 | 0.176 | 1.010 | 0 | 0 | 0.98307 | 0.01693 | 0.98170 | 0.01830 | 1 | 0.01693 | 0.00029 | 0.50475 |
| 22 | 0 | 0.90 | 0.93 | 0.84 | 0.6 | 1.591 | 1.020 | 0 | 0 | 0.99378 | 0.00622 | 0.99348 | 0.00652 | 1 | 0.00622 | 0.00003 | 0.56062 |
| 23 | 1 | 1.00 | 0.58 | 0.58 | 1.0 | 0.531 | 1.002 | 1 | 0 | 0.74739 | 0.25261 | 0.84423 | 0.15577 | 1 | 0.25261 | 0.06137 | 0.63597 |
| 24 | 0 | 0.95 | 0.32 | 0.30 | 1.6 | 0.886 | 0.988 | 0 | 1 | 0.12989 | 0.87011 | 0.03637 | 0.96363 | 1 | 0.87011 | 0.40910 | 0.98481 |
| 25 | 1 | 1.00 | 0.60 | 0.60 | 1.7 | 0.964 | 0.990 | 1 | 1 | 0.06868 | 0.93132 | 0.08017 | 0.91983 | 1 | 0.93132 | 0.44114 | 0.99573 |
| 26 | 1 | 1.00 | 0.69 | 0.69 | 0.9 | 0.398 | 0.986 | 1 | 0 | 0.53949 | 0.46051 | 0.62312 | 0.37688 | 1 | 0.46051 | 0.16612 | 0.78529 |
| 27 | 0 | 1.00 | 0.73 | 0.73 | 0.7 | 0.398 | 0.986 | 0 | 0 | 0.71742 | 0.28258 | 0.67259 | 0.32741 | 1 | 0.28258 | 0.07498 | 0.65683 |
If you want to order the selected models based on a statistic such as the AIC, R-square, or area under the ROC curve (AUC),
you can use the ODS OUTPUT statement to save the appropriate table to a data set and then display the statistic along with
the step number. For example, the following program orders the steps according to the "c" statistic from the Association data set:
data Association(rename=(Label2=Statistic nValue2=Value)); set Association; if (Label2='c'); keep Step Label2 nValue2; proc sort data=Association; by Value; title; proc print data=Association; run;
The results, displayed in Output 72.1.9, show that the model that has the largest AUC (0.889) is the final model selected by the stepwise method. You can also perform this analysis by using the %SELECT macro (SAS Institute Inc. 2015).
Output 72.1.9: Selection Steps Ordered by AUC
Next, a different variable selection method is used to select prognostic factors for cancer remission, and an efficient algorithm is employed to eliminate insignificant variables from a model. The following statements invoke PROC LOGISTIC to perform the backward elimination analysis:
title 'Backward Elimination on Cancer Remission Data';
proc logistic data=Remission;
model remiss(event='1')=temp cell li smear blast
/ selection=backward fast slstay=0.2 ctable;
run;
The backward elimination analysis (SELECTION= BACKWARD) starts with a model that contains all explanatory variables given in the MODEL statement. By specifying the FAST option, PROC LOGISTIC eliminates insignificant variables without refitting the model repeatedly. This analysis uses a significance level of 0.2 to retain variables in the model (SLSTAY= 0.2), which is different from the previous stepwise analysis where SLSTAY=.35. The CTABLE option is specified to produce classifications of input observations based on the final selected model.
Results of the fast elimination analysis are shown in Output 72.1.10 and Output 72.1.11. Initially, a full model containing all six risk factors is fit to the data (Output 72.1.10). In the next step (Output 72.1.11), PROC LOGISTIC removes blast, smear, cell, and temp from the model all at once. This leaves li and the intercept as the only variables in the final model. Note that in this analysis, only parameter estimates for the
final model are displayed because the DETAILS
option has not been specified.
Output 72.1.10: Initial Step in Backward Elimination
Output 72.1.11: Fast Elimination Step
|
Step 1. Fast Backward Elimination: |
| Analysis of Effects Removed by Fast Backward Elimination | ||||||
|---|---|---|---|---|---|---|
| Effect Removed |
Chi-Square | DF | Pr > ChiSq | Residual Chi-Square |
DF | Pr > Residual ChiSq |
| blast | 0.0008 | 1 | 0.9768 | 0.0008 | 1 | 0.9768 |
| smear | 0.0951 | 1 | 0.7578 | 0.0959 | 2 | 0.9532 |
| cell | 1.5134 | 1 | 0.2186 | 1.6094 | 3 | 0.6573 |
| temp | 0.6535 | 1 | 0.4189 | 2.2628 | 4 | 0.6875 |
Note that you can also use the FAST option when SELECTION= STEPWISE. However, the FAST option operates only on backward elimination steps. In this example, the stepwise process only adds variables, so the FAST option would not be useful.
Results of the CTABLE option are shown in Output 72.1.12.
Output 72.1.12: Classifying Input Observations
| Classification Table | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Prob Level |
Correct | Incorrect | Percentages | ||||||
| Event | Non- Event |
Event | Non- Event |
Correct | Sensi- tivity |
Speci- ficity |
False POS |
False NEG |
|
| 0.060 | 9 | 0 | 18 | 0 | 33.3 | 100.0 | 0.0 | 66.7 | . |
| 0.080 | 9 | 2 | 16 | 0 | 40.7 | 100.0 | 11.1 | 64.0 | 0.0 |
| 0.100 | 9 | 4 | 14 | 0 | 48.1 | 100.0 | 22.2 | 60.9 | 0.0 |
| 0.120 | 9 | 4 | 14 | 0 | 48.1 | 100.0 | 22.2 | 60.9 | 0.0 |
| 0.140 | 9 | 7 | 11 | 0 | 59.3 | 100.0 | 38.9 | 55.0 | 0.0 |
| 0.160 | 9 | 10 | 8 | 0 | 70.4 | 100.0 | 55.6 | 47.1 | 0.0 |
| 0.180 | 9 | 10 | 8 | 0 | 70.4 | 100.0 | 55.6 | 47.1 | 0.0 |
| 0.200 | 8 | 13 | 5 | 1 | 77.8 | 88.9 | 72.2 | 38.5 | 7.1 |
| 0.220 | 8 | 13 | 5 | 1 | 77.8 | 88.9 | 72.2 | 38.5 | 7.1 |
| 0.240 | 8 | 13 | 5 | 1 | 77.8 | 88.9 | 72.2 | 38.5 | 7.1 |
| 0.260 | 6 | 13 | 5 | 3 | 70.4 | 66.7 | 72.2 | 45.5 | 18.8 |
| 0.280 | 6 | 13 | 5 | 3 | 70.4 | 66.7 | 72.2 | 45.5 | 18.8 |
| 0.300 | 6 | 13 | 5 | 3 | 70.4 | 66.7 | 72.2 | 45.5 | 18.8 |
| 0.320 | 6 | 14 | 4 | 3 | 74.1 | 66.7 | 77.8 | 40.0 | 17.6 |
| 0.340 | 5 | 14 | 4 | 4 | 70.4 | 55.6 | 77.8 | 44.4 | 22.2 |
| 0.360 | 5 | 14 | 4 | 4 | 70.4 | 55.6 | 77.8 | 44.4 | 22.2 |
| 0.380 | 5 | 15 | 3 | 4 | 74.1 | 55.6 | 83.3 | 37.5 | 21.1 |
| 0.400 | 5 | 15 | 3 | 4 | 74.1 | 55.6 | 83.3 | 37.5 | 21.1 |
| 0.420 | 5 | 15 | 3 | 4 | 74.1 | 55.6 | 83.3 | 37.5 | 21.1 |
| 0.440 | 5 | 15 | 3 | 4 | 74.1 | 55.6 | 83.3 | 37.5 | 21.1 |
| 0.460 | 4 | 16 | 2 | 5 | 74.1 | 44.4 | 88.9 | 33.3 | 23.8 |
| 0.480 | 4 | 16 | 2 | 5 | 74.1 | 44.4 | 88.9 | 33.3 | 23.8 |
| 0.500 | 4 | 16 | 2 | 5 | 74.1 | 44.4 | 88.9 | 33.3 | 23.8 |
| 0.520 | 4 | 16 | 2 | 5 | 74.1 | 44.4 | 88.9 | 33.3 | 23.8 |
| 0.540 | 3 | 16 | 2 | 6 | 70.4 | 33.3 | 88.9 | 40.0 | 27.3 |
| 0.560 | 3 | 16 | 2 | 6 | 70.4 | 33.3 | 88.9 | 40.0 | 27.3 |
| 0.580 | 3 | 16 | 2 | 6 | 70.4 | 33.3 | 88.9 | 40.0 | 27.3 |
| 0.600 | 3 | 16 | 2 | 6 | 70.4 | 33.3 | 88.9 | 40.0 | 27.3 |
| 0.620 | 3 | 16 | 2 | 6 | 70.4 | 33.3 | 88.9 | 40.0 | 27.3 |
| 0.640 | 3 | 16 | 2 | 6 | 70.4 | 33.3 | 88.9 | 40.0 | 27.3 |
| 0.660 | 3 | 16 | 2 | 6 | 70.4 | 33.3 | 88.9 | 40.0 | 27.3 |
| 0.680 | 3 | 16 | 2 | 6 | 70.4 | 33.3 | 88.9 | 40.0 | 27.3 |
| 0.700 | 3 | 16 | 2 | 6 | 70.4 | 33.3 | 88.9 | 40.0 | 27.3 |
| 0.720 | 2 | 16 | 2 | 7 | 66.7 | 22.2 | 88.9 | 50.0 | 30.4 |
| 0.740 | 2 | 16 | 2 | 7 | 66.7 | 22.2 | 88.9 | 50.0 | 30.4 |
| 0.760 | 2 | 16 | 2 | 7 | 66.7 | 22.2 | 88.9 | 50.0 | 30.4 |
| 0.780 | 2 | 16 | 2 | 7 | 66.7 | 22.2 | 88.9 | 50.0 | 30.4 |
| 0.800 | 2 | 17 | 1 | 7 | 70.4 | 22.2 | 94.4 | 33.3 | 29.2 |
| 0.820 | 2 | 17 | 1 | 7 | 70.4 | 22.2 | 94.4 | 33.3 | 29.2 |
| 0.840 | 0 | 17 | 1 | 9 | 63.0 | 0.0 | 94.4 | 100.0 | 34.6 |
| 0.860 | 0 | 17 | 1 | 9 | 63.0 | 0.0 | 94.4 | 100.0 | 34.6 |
| 0.880 | 0 | 17 | 1 | 9 | 63.0 | 0.0 | 94.4 | 100.0 | 34.6 |
| 0.900 | 0 | 17 | 1 | 9 | 63.0 | 0.0 | 94.4 | 100.0 | 34.6 |
| 0.920 | 0 | 17 | 1 | 9 | 63.0 | 0.0 | 94.4 | 100.0 | 34.6 |
| 0.940 | 0 | 17 | 1 | 9 | 63.0 | 0.0 | 94.4 | 100.0 | 34.6 |
| 0.960 | 0 | 18 | 0 | 9 | 66.7 | 0.0 | 100.0 | . | 33.3 |
Each row of the "Classification Table" corresponds to a cutpoint applied to the predicted probabilities, which is given in
the Prob Level column. The  frequency tables of observed and predicted responses are given by the next four columns. For example, with a cutpoint of
0.5, 4 events and 16 nonevents were classified correctly. On the other hand, 2 nonevents were incorrectly classified as events
and 5 events were incorrectly classified as nonevents. For this cutpoint, the correct classification rate is 20/27 (=74.1%),
which is given in the sixth column. Accuracy of the classification is summarized by the sensitivity, specificity, and false
positive and negative rates, which are displayed in the last four columns. You can control the number of cutpoints used, and
their values, by using the PPROB=
option.
frequency tables of observed and predicted responses are given by the next four columns. For example, with a cutpoint of
0.5, 4 events and 16 nonevents were classified correctly. On the other hand, 2 nonevents were incorrectly classified as events
and 5 events were incorrectly classified as nonevents. For this cutpoint, the correct classification rate is 20/27 (=74.1%),
which is given in the sixth column. Accuracy of the classification is summarized by the sensitivity, specificity, and false
positive and negative rates, which are displayed in the last four columns. You can control the number of cutpoints used, and
their values, by using the PPROB=
option.