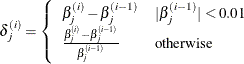-
ABSFCONV=value
-
specifies the absolute function convergence criterion. Convergence requires a small change in the log-likelihood function
in subsequent iterations,
where 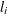 is the value of the log-likelihood function at iteration i. See the section Convergence Criteria for more information.
is the value of the log-likelihood function at iteration i. See the section Convergence Criteria for more information.
-
AGGREGATE<=(variable-list)>
-
specifies the subpopulations on which the Pearson chi-square test statistic and the likelihood ratio chi-square test statistic
(deviance) are calculated. Observations with common values in the given list of variables are regarded as coming from the
same subpopulation. Variables in the list can be any variables in the input data set. Specifying the AGGREGATE option is equivalent
to specifying the AGGREGATE= option with a variable list that includes all explanatory variables in the MODEL statement. The
deviance and Pearson goodness-of-fit statistics
are calculated only when the SCALE=
option is specified. Thus, the AGGREGATE (or AGGREGATE=) option has no effect if the SCALE=
option is not specified.
See the section Rescaling the Covariance Matrix for more information.
-
ALPHA=number
-
sets the level of significance  for
for 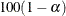 % confidence intervals for regression parameters or odds ratios. The value of number must be between 0 and 1. By default, number is equal to the value of the ALPHA=
option in the PROC LOGISTIC statement, or 0.05 if the option is not specified. This option has no effect unless confidence
limits for the parameters (CLPARM=
option) or odds ratios (CLODDS=
option or ODDSRATIO
statement) are requested.
% confidence intervals for regression parameters or odds ratios. The value of number must be between 0 and 1. By default, number is equal to the value of the ALPHA=
option in the PROC LOGISTIC statement, or 0.05 if the option is not specified. This option has no effect unless confidence
limits for the parameters (CLPARM=
option) or odds ratios (CLODDS=
option or ODDSRATIO
statement) are requested.
-
BEST=number
-
specifies that number models with the highest score chi-square statistics are to be displayed for each model size. It is used exclusively with
the SCORE
model selection method. If the BEST= option is omitted and there are no more than 10 explanatory variables, then all possible
models are listed for each model size. If the option is omitted and there are more than 10 explanatory variables, then the
number of models selected for each model size is, at most, equal to the number of explanatory variables listed in the MODEL
statement.
-
BINWIDTH=width
-
specifies the size of the bins used for estimating the association statistics. For more information, see the section Rank Correlation of Observed Responses and Predicted Probabilities. Valid values are 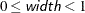 (for polytomous response models,
(for polytomous response models, 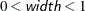 ). In releases before SAS/STAT 14.1, the default width is 0.002. Beginning in SAS/STAT 14.1, if you have a binary response and fewer than 5,000,000 observations, the default is
BINWIDTH=0; this means that no binning is performed and the exact values of the statistics are computed using the trapezoidal
area described in the section ROC Computations. This method is a bit slower and might require more memory than the binning approach.
). In releases before SAS/STAT 14.1, the default width is 0.002. Beginning in SAS/STAT 14.1, if you have a binary response and fewer than 5,000,000 observations, the default is
BINWIDTH=0; this means that no binning is performed and the exact values of the statistics are computed using the trapezoidal
area described in the section ROC Computations. This method is a bit slower and might require more memory than the binning approach.
If a nonzero width does not evenly divide the unit interval, it is reduced to a valid value and a message is displayed in the SAS log. The number
of bins is also constrained by the amount of memory available on your machine; if a nonzero width is so small that you cannot allocate 8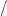 width bytes of memory for the bins, then width is adjusted to a value for which memory can be allocated and a note is displayed in the SAS log.
width bytes of memory for the bins, then width is adjusted to a value for which memory can be allocated and a note is displayed in the SAS log.
The BINWIDTH= option is ignored and no binning is performed when a ROC
statement is specified, when ROC graphics are produced, or when the SCORE
statement computes an ROC area.
-
CLODDS=PL | WALD | BOTH
-
produces confidence intervals for odds ratios of main effects not involved in interactions or nestings. Computation of these
confidence intervals is based on the profile likelihood (CLODDS=PL) or based on individual Wald tests (CLODDS=WALD). By specifying
CLODDS=BOTH, the procedure computes two sets of confidence intervals for the odds ratios, one based on the profile likelihood
and the other based on the Wald tests. The confidence coefficient can be specified with the ALPHA=
option. The CLODDS=PL option is not available with the STRATA
statement. Classification main effects that use parameterizations other than REF, EFFECT, or GLM are ignored. If you need
to compute odds ratios for an effect involved in interactions or nestings, or using some other parameterization, then you
should specify an ODDSRATIO
statement for that effect.
-
CLPARM=PL | WALD | BOTH
-
requests confidence intervals for the parameters. Computation of these confidence intervals is based on the profile likelihood
(CLPARM=PL) or individual Wald tests (CLPARM=WALD). If you specify CLPARM=BOTH, the procedure computes two sets of confidence
intervals for the parameters, one based on the profile likelihood and the other based on individual Wald tests. The confidence
coefficient can be specified with the ALPHA=
option. The CLPARM=PL option is not available with the STRATA
statement.
See the section Confidence Intervals for Parameters for more information.
-
CORRB
-
displays the correlation matrix of the parameter estimates.
-
COVB
-
displays the covariance matrix of the parameter estimates.
-
CTABLE
-
classifies the input binary response observations according to whether the predicted event probabilities are above or below
some cutpoint value z in the range 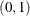 . An observation is predicted as an event if the predicted event probability exceeds or equals z. You can supply a list of cutpoints other than the default list by specifying the PPROB= option
. Also, false positive and negative rates can be computed as posterior probabilities by using Bayes’ theorem. You can use
the PEVENT=
option to specify prior probabilities for computing these rates. The CTABLE option is ignored if the data have more than
two response levels. The CTABLE option is not available with the STRATA
statement.
. An observation is predicted as an event if the predicted event probability exceeds or equals z. You can supply a list of cutpoints other than the default list by specifying the PPROB= option
. Also, false positive and negative rates can be computed as posterior probabilities by using Bayes’ theorem. You can use
the PEVENT=
option to specify prior probabilities for computing these rates. The CTABLE option is ignored if the data have more than
two response levels. The CTABLE option is not available with the STRATA
statement.
For more information, see the section Classification Table.
-
DETAILS
-
produces a summary of computational details for each step of the effect selection process. It produces the "Analysis of Effects
Eligible for Entry" table before displaying the effect selected for entry for forward or stepwise selection. For each model
fitted, it produces the "Joint Tests" or "Type 3 Analysis of Effects" table if the fitted model involves CLASS variables,
the "Analysis of Maximum Likelihood Estimates" table, and measures of association between predicted probabilities and observed
responses. For the statistics included in these tables, see the section Displayed Output. The DETAILS option has no effect when SELECTION=
NONE.
-
EQUALSLOPES<=effect | (effect-list)>
-
specifies one or more effects that have the same parameters for each response function in a polytomous response model. If
you specify more than one effect, enclose the effects in parentheses. The effects must be explanatory effects that are specified
in the MODEL statement.
If you do not specify this option, the generalized logit model (LINK=GLOGIT
) makes the unequal slopes assumption, 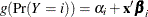 , where the response functions have different slope parameters
, where the response functions have different slope parameters 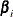 . If you specify this option without an effect or effect-list, all slope parameters are shared across the response functions, resulting in the model
. If you specify this option without an effect or effect-list, all slope parameters are shared across the response functions, resulting in the model 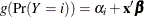 . Specifying an effect or effect-list enables you to choose which effects have the same parameters across the response functions. For any specified selection method,
equal slope parameters can contain and be contained in only other equal slope parameters; for more information, see the HIERARCHY=
option.
. Specifying an effect or effect-list enables you to choose which effects have the same parameters across the response functions. For any specified selection method,
equal slope parameters can contain and be contained in only other equal slope parameters; for more information, see the HIERARCHY=
option.
You can specify the EQUALSLOPES option along with the UNEQUALSLOPES
option to create an effect that has both equal and unequal slopes. In this case, the parameters that have equal slopes model
the mean effect across the response functions, whereas the parameters that have unequal slopes model deviations from the mean.
For more information, see the UNEQUALSLOPES
option.
For an example that uses this option, see Example 72.18. If you specify the EQUALSLOPES option, you cannot specify any of the EFFECTPLOT, ESTIMATE, EXACT, LSMEANS, LSMESTIMATE,
ROC, ROCCONTRAST, SLICE, STORE, and STRATA statements, and you cannot specify the following options: CTABLE, FIRTH, OUTROC=, PEVENT=, PPROB=, RIDGING=, and TECHNIQUE=.
-
EXPB
EXPEST
-
displays the exponentiated values (e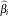 ) of the parameter estimates
) of the parameter estimates 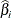 in the "Analysis of Maximum Likelihood Estimates" table for the logit model. These exponentiated values are the estimated
odds ratios for parameters corresponding to the continuous explanatory variables, and for CLASS effects that use reference
or GLM parameterizations.
in the "Analysis of Maximum Likelihood Estimates" table for the logit model. These exponentiated values are the estimated
odds ratios for parameters corresponding to the continuous explanatory variables, and for CLASS effects that use reference
or GLM parameterizations.
-
FAST
-
uses a computational algorithm of Lawless and Singhal (1978) to compute a first-order approximation to the remaining slope estimates for each subsequent elimination of a variable from
the model. Variables are removed from the model based on these approximate estimates. The FAST option is extremely efficient
because the model is not refitted for every variable removed. The FAST option is used when SELECTION=
BACKWARD and in the backward elimination steps when SELECTION=
STEPWISE. The FAST option is ignored when SELECTION=
FORWARD or SELECTION=
NONE.
-
FCONV=value
-
specifies the relative function convergence criterion. Convergence requires a small relative change in the log-likelihood
function in subsequent iterations,
where 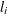 is the value of the log likelihood at iteration i. See the section Convergence Criteria for more information.
is the value of the log likelihood at iteration i. See the section Convergence Criteria for more information.
-
FIRTH
-
performs Firth’s penalized maximum likelihood estimation to reduce bias in the parameter estimates (Heinze and Schemper 2002; Firth 1993). This method is useful in cases of separability, as often occurs when the event is rare, and is an alternative to performing
an exact logistic regression. See the section Firth’s Bias-Reducing Penalized Likelihood for more information.
Note: The intercept-only log likelihood is modified by using the full-model Hessian, computed with the slope parameters equal
to zero. When fitting a model and scoring a data set in the same PROC LOGISTIC step, the model is fit using Firth’s penalty
for parameter estimation purposes, but the penalty is not applied to the scored log likelihood.
-
GCONV=value
-
specifies the relative gradient convergence criterion. Convergence requires that the normalized prediction function reduction
is small,
where 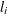 is the value of the log-likelihood function,
is the value of the log-likelihood function, 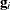 is the gradient vector, and
is the gradient vector, and 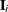 is the negative (expected) Hessian matrix, all at iteration i. This is the default convergence criterion, and the default value is 1E–8. See the section Convergence Criteria for more information.
is the negative (expected) Hessian matrix, all at iteration i. This is the default convergence criterion, and the default value is 1E–8. See the section Convergence Criteria for more information.
-
HIERARCHY=keyword
HIER=keyword
-
specifies whether and how the model hierarchy requirement is applied and whether a single effect or multiple effects are allowed
to enter or leave the model in one step. You can specify that only CLASS effects, or both CLASS and interval effects, be subject
to the hierarchy requirement. The HIERARCHY= option is ignored unless you also specify one of the following options: SELECTION=
FORWARD, SELECTION=
BACKWARD, or SELECTION=
STEPWISE.
Model hierarchy refers to the requirement that, for any term to be in the model, all effects contained in the term must be
present in the model. For example, in order for the interaction A*B to enter the model, the main effects A and B must be in
the model. Likewise, neither effect A nor B can leave the model while the interaction A*B is in the model.
The keywords you can specify in the HIERARCHY= option are as follows:
- NONE
-
indicates that the model hierarchy is not maintained. Any single effect can enter or leave the model at any given step of
the selection process.
- SINGLE
-
indicates that only one effect can enter or leave the model at one time, subject to the model hierarchy requirement. For example,
suppose that you specify the main effects A and B and the interaction A*B in the model. In the first step of the selection
process, either A or B can enter the model. In the second step, the other main effect can enter the model. The interaction
effect can enter the model only when both main effects have already been entered. Also, before A or B can be removed from
the model, the A*B interaction must first be removed. All effects (CLASS and interval) are subject to the hierarchy requirement.
- SINGLECLASS
-
is the same as HIERARCHY=SINGLE except that only CLASS effects are subject to the hierarchy requirement.
- MULTIPLE
-
indicates that more than one effect can enter or leave the model at one time, subject to the model hierarchy requirement.
In a forward selection step, a single main effect can enter the model, or an interaction can enter the model together with
all the effects that are contained in the interaction. In a backward elimination step, an interaction itself, or the interaction
together with all the effects that the interaction contains, can be removed. All effects (CLASS and continuous) are subject
to the hierarchy requirement.
- MULTIPLECLASS
-
is the same as HIERARCHY=MULTIPLE except that only CLASS effects are subject to the hierarchy requirement.
The default value is HIERARCHY=SINGLE, which means that model hierarchy is to be maintained for all effects (that is, both
CLASS and continuous effects) and that only a single effect can enter or leave the model at each step.
-
INCLUDE=number | EQUALSLOPES
-
specifies effects in the MODEL statement to include in every model during model selection. You can specify the following values:
- number
-
requests that the first number effects be included in every model.
- EQUALSLOPES
-
enables you to include all the equal slope effects in every model and perform the selection process on the unequal slope effects.
By default, INCLUDE=0. The INCLUDE= option has no effect when SELECTION=
NONE. You cannot specify the INCLUDE=EQUALSLOPES option if you specify SELECTION=SCORE
.
If you specify the same effect in both the EQUALSLOPES
and UNEQUALSLOPES
options, then that effect is treated as two separate effects. For example, suppose you specify the following MODEL statement:
model Y=X1 X2 / equalslopes unequalslopes selection=forward;
The X1 and X2 variables both generate an equal slope effect and an unequal slope effect. Specifying INCLUDE=1 includes the
equal slope effect for X1 in every model; specifying INCLUDE=2 includes both the equal and unequal slope effects for X1 in
every model; specifying INCLUDE=EQUALSLOPES includes the equal slope effects for X1 and for X2 in every model.
Note that the INCLUDE= and START=
options perform different tasks: the INCLUDE= option includes effects in every model, whereas the START= option requires
only that the effects appear in the first model.
-
INFLUENCE<(STDRES)>
-
displays diagnostic measures for identifying influential observations in the case of a binary response model. For each observation,
the INFLUENCE option displays the case number (which is the sequence number of the observation), the values of the explanatory
variables included in the final model, and the regression diagnostic measures developed by Pregibon (1981). The STDRES option includes standardized and likelihood residuals in the display.
For a discussion of these diagnostic measures, see the section Regression Diagnostics. When a STRATA
statement is specified, the diagnostics are computed following Storer and Crowley (1985); for more information, see the section Regression Diagnostic Details.
-
IPLOTS
-
produces an index plot for the regression diagnostic statistics developed by Pregibon (1981). An index plot is a scatter plot with the regression diagnostic statistic represented on the Y axis and the case number
on the X axis. See Example 72.6 for an illustration.
-
ITPRINT
-
displays the iteration history of the maximum-likelihood model fitting. The ITPRINT option also displays the last evaluation
of the gradient vector and the final change in the –2 Log Likelihood.
-
LACKFIT<(number)>
-
performs the Hosmer and Lemeshow goodness-of-fit test (Hosmer and Lemeshow 2000) for the case of a binary response model. The subjects are divided into approximately 10 groups of roughly the same size
based on the percentiles of the estimated probabilities. The discrepancies between the observed and expected number of observations
in these groups are summarized by the Pearson chi-square statistic, which is then compared to a chi-square distribution with
t degrees of freedom, where t is the number of groups minus number. By default, number = 2. A small p-value suggests that the fitted model is not an adequate model. The LACKFIT option is not available with the STRATA
statement. See the section The Hosmer-Lemeshow Goodness-of-Fit Test for more information.
-
LINK=keyword
L=keyword
-
specifies the link function linking the response probabilities to the linear predictors. You can specify one of the following
keywords. The default is LINK=LOGIT.
- ALOGIT
-
is the adjacent-category logit function. PROC LOGISTIC fits the adjacent-category logit model, in which each category is contrasted
with the following category.
- CLOGLOG
-
is the complementary log-log function. PROC LOGISTIC fits the binary complementary log-log model when there are two response
categories and fits the cumulative complementary log-log model when there are more than two response categories. The aliases
are CCLOGLOG, CCLL, and CUMCLOGLOG.
- GLOGIT
-
is the generalized logit function. PROC LOGISTIC fits the generalized logit model, in which each nonreference category is
contrasted with the reference category. You can use the response variable option REF=
to specify the reference category.
- LOGIT
-
is the log odds function. PROC LOGISTIC fits the binary logit model when there are two response categories and fits the cumulative
logit model when there are more than two response categories. The aliases are CLOGIT and CUMLOGIT.
- PROBIT
-
is the inverse standard normal distribution function. PROC LOGISTIC fits the binary probit model when there are two response
categories and fits the cumulative probit model when there are more than two response categories. The aliases are NORMIT,
CPROBIT, and CUMPROBIT.
The LINK= option is not available with the STRATA
statement.
For more information, see the section Link Functions and the Corresponding Distributions.
-
MAXFUNCTION=number
-
specifies the maximum number of function calls to perform when maximizing the conditional likelihood. This option is valid
only when you specify an EQUALSLOPES
or UNEQUALSLOPES
option, or you specify a STRATA
statement. The default values are as follows:
Because the optimization is terminated only after completing a full iteration, the number of function calls that are actually
performed can exceed number. If convergence is not attained, the displayed output and all output data sets that PROC LOGISTIC creates contain results
that are based on the last maximum likelihood iteration.
-
MAXITER=number
-
specifies the maximum number of iterations to perform. By default, MAXITER=25. If convergence is not attained in number iterations, the displayed output and all output data sets created by the procedure contain results that are based on the
last maximum likelihood iteration.
-
MAXSTEP=number
-
specifies the maximum number of times any explanatory variable is added to or removed from the model when SELECTION=
STEPWISE. The default number is twice the number of explanatory variables in the MODEL statement. When the MAXSTEP= limit
is reached, the stepwise selection process is terminated. All statistics displayed by the procedure (and included in output
data sets) are based on the last model fitted. The MAXSTEP= option has no effect when SELECTION=
NONE, FORWARD, or BACKWARD.
-
NOCHECK
-
disables the checking process to determine whether maximum likelihood estimates of the regression parameters exist. If you
are sure that the estimates are finite, this option can reduce the execution time if the estimation takes more than eight
iterations. For more information, see the section Existence of Maximum Likelihood Estimates.
-
NODUMMYPRINT
NODESIGNPRINT
NODP
-
suppresses the "Class Level Information" table, which shows how the design matrix columns for the CLASS variables are coded.
-
NOINT
-
suppresses the intercept for the binary response model, the first intercept for the ordinal response model (which forces all
intercepts to be nonnegative), or all intercepts for the generalized logit model. This can be particularly useful in conditional
logistic analysis; see Example 72.11.
-
NOFIT
-
performs the global score test without fitting the model. The global score test evaluates the joint significance of the effects
in the MODEL statement. No further analyses are performed. If the NOFIT option is specified along with other MODEL statement
options, NOFIT takes effect and all other options except FIRTH, LINK=, NOINT, OFFSET=, and TECHNIQUE= are ignored. The NOFIT
option is not available with the STRATA
statement.
-
NOLOGSCALE
-
specifies that computations for the conditional and exact logistic regression models should be computed by using normal scaling.
Log scaling can handle numerically larger problems than normal scaling; however, computations in the log scale are slower
than computations in normal scale.
-
NOODDSRATIO
NOOR
-
suppresses the default "Odds Ratio" table.
-
OFFSET=name
-
names the offset variable. The regression coefficient for this variable will be fixed at 1. For an example that uses this
option, see Example 72.14. You can also use the OFFSET= option to restrict parameters to a fixed value. For example, if you want to restrict the parameter
for variable X1 to 1 and the parameter for X2 to 2, compute Restrict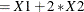 in a DATA step, specify the option
in a DATA step, specify the option offset=Restrict, and leave X1 and X2 out of the model.
-
ORPVALUE
-
displays p-values in tables produced by the CLODDS=
option and the ODDSRATIO
statement. A p-value for an odds ratio corresponds to the significance level such that the two-sided confidence interval for the odds ratio
has "1" as one of its endpoints. Computing profile-likelihood p-values requires optimizing restricted log-likelihood equations; for more information, see the section Confidence Intervals for Parameters. This option is not available with the FIRTH option.
-
OUTROC=SAS-data-set
OUTR=SAS-data-set
-
creates, for binary response models, an output SAS data set that contains the data necessary to produce the receiver operating
characteristic (ROC)
curve. The OUTROC= option is not available with the STRATA
statement. See the section OUTROC= Output Data Set for the list of variables in this data set.
-
PARMLABEL
-
displays the labels of the parameters in the "Analysis of Maximum Likelihood Estimates" table.
-
PCORR
-
computes the partial correlation statistic 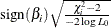 for each parameter i, where
for each parameter i, where 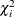 is the Wald chi-square statistic for the parameter and
is the Wald chi-square statistic for the parameter and 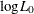 is the log-likelihood of the intercept-only model (Hilbe 2009, p. 101). If
is the log-likelihood of the intercept-only model (Hilbe 2009, p. 101). If 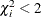 then the partial correlation is set to 0. The partial correlation for the intercept terms is set to missing.
then the partial correlation is set to 0. The partial correlation for the intercept terms is set to missing.
-
PEVENT=value| (list)
-
specifies one prior probability or a list of prior probabilities for the event of interest. The false positive and false negative
rates are then computed as posterior probabilities by Bayes’ theorem. The prior probability is also used in computing the
rate of correct prediction. For each prior probability in the given list, a classification table of all observations is computed.
By default, the prior probability is the total sample proportion of events. The PEVENT= option is useful for stratified samples.
It has no effect if the CTABLE option is not specified. For more information, see the section False Positive, False Negative, and Correct Classification Rates Using Bayes’ Theorem. Also see the PPROB= option
for information about how the list is specified.
-
PLCL
-
is the same as specifying CLPARM=PL
.
-
PLCONV=value
-
controls the convergence criterion for confidence intervals based on the profile-likelihood function. The quantity value must be a positive number, with a default value of 1E–4. The PLCONV= option has no effect if profile-likelihood confidence
intervals (CLPARM=PL
) are not requested.
-
PLRL
-
is the same as specifying CLODDS=PL
.
-
PPROB=value | (list)
-
specifies one critical probability value (or cutpoint) or a list of critical probability values for classifying observations
with the CTABLE
option. Each value must be between 0 and 1. A response that has a cross validated predicted probability greater than or equal to the current
PPROB= value is classified as an event response. The PPROB= option is ignored if the CTABLE
option is not specified.
A classification table for each of several cutpoints can be requested by specifying a list. For example, the following statement
requests a classification of the observations for each of the cutpoints 0.3, 0.5, 0.6, 0.7, and 0.8:
pprob= (0.3, 0.5 to 0.8 by 0.1)
If the PPROB= option is not specified, the default is to display the classification for a range of probabilities from the
smallest estimated probability (rounded down to the nearest 0.02) to the highest estimated probability (rounded up to the
nearest 0.02) with 0.02 increments.
-
RIDGING=ABSOLUTE | RELATIVE | NONE
-
specifies the technique used to improve the log-likelihood function when its value in the current iteration is less than that
in the previous iteration. If you specify the RIDGING=ABSOLUTE option, the diagonal elements of the negative (expected) Hessian
are inflated by adding the ridge value. If you specify the RIDGING=RELATIVE option, the diagonal elements are inflated by
a factor of 1 plus the ridge value. If you specify the RIDGING=NONE option, the crude line search method of taking half a
step is used instead of ridging. By default, RIDGING=RELATIVE.
-
RISKLIMITS
RL
WALDRL
-
is the same as specifying CLODDS=WALD
.
-
ROCCI
-
displays standard errors and confidence limits for the area under the ROC curve (AUC) statistic when you have a binary response
variable. This option replaces the "Association of Predicted Probabilities and Observed Responses" table with the "ROC Association
Statistics" table.
-
ROCEPS=number
-
specifies a criterion for the ROC curve used for grouping estimated event probabilities that are close to each other. In each
group, the difference between the largest and the smallest estimated event probabilities does not exceed the given value.
The value for number must be between 0 and 1; the default value is the square root of the machine epsilon, which is about 1E–8 (in releases prior
to 9.2, the default was 1E–4). The smallest estimated probability in each group serves as a cutpoint for predicting an event
response. The ROCEPS= option has no effect unless the OUTROC=
option, the BINWIDTH=0
option, or a ROC statement
is specified.
-
RSQUARE
RSQ
-
requests a generalized R-square measure for the fitted model. For more information, see the section Generalized Coefficient of Determination.
-
SCALE=scale
-
enables you to supply the value of the dispersion parameter or to specify the method for estimating the dispersion parameter.
It also enables you to display the "Deviance and Pearson Goodness-of-Fit Statistics" table. To correct for overdispersion
or underdispersion, the covariance matrix is multiplied by the estimate of the dispersion parameter. Valid values for scale are as follows:
- D | DEVIANCE
-
specifies that the dispersion parameter be estimated by the deviance divided by its degrees of freedom.
- P | PEARSON
-
specifies that the dispersion parameter be estimated by the Pearson chi-square statistic divided by its degrees of freedom.
- WILLIAMS <(constant)>
-
specifies that Williams’ method be used to model overdispersion. This option can be used only with the events/trials syntax.
An optional constant can be specified as the scale parameter; otherwise, a scale parameter is estimated under the full model. A set of weights
is created based on this scale parameter estimate. These weights can then be used in fitting subsequent models of fewer terms
than the full model. When fitting these submodels, specify the computed scale parameter as constant. See Example 72.10 for an illustration.
- N | NONE
-
specifies that no correction is needed for the dispersion parameter; that is, the dispersion parameter remains as 1. This
specification is used for requesting the deviance and the Pearson chi-square statistic without adjusting for overdispersion.
- constant
-
sets the estimate of the dispersion parameter to be the square of the given constant. For example, SCALE=2 sets the dispersion parameter to 4. The value constant must be a positive number.
You can use the AGGREGATE
(or AGGREGATE=) option to
define the subpopulations for calculating the Pearson chi-square statistic and the deviance. In the absence of the AGGREGATE
(or AGGREGATE=) option, each observation is regarded as coming from a different subpopulation. For the events/trials syntax,
each observation consists of n Bernoulli trials, where n is the value of the trials variable. For single-trial syntax, each observation consists of a single response, and for this setting it is not appropriate
to carry out the Pearson or deviance goodness-of-fit analysis. Thus, PROC LOGISTIC ignores specifications SCALE=P, SCALE=D,
and SCALE=N when single-trial syntax is specified without the AGGREGATE
(or AGGREGATE=) option.
The "Deviance and Pearson Goodness-of-Fit Statistics" table includes the
Pearson chi-square statistic, the deviance, the degrees of freedom, the ratio of each statistic divided by its degrees of
freedom, and the corresponding p-value. The SCALE= option is not available with the STRATA
statement. For more information, see the section Overdispersion.
-
SELECTION=BACKWARD | B
| FORWARD | F
| NONE | N
| STEPWISE | S
| SCORE
-
specifies the method used to select the variables in the model. BACKWARD requests backward elimination, FORWARD requests forward
selection, NONE fits the complete model specified in the MODEL statement, and STEPWISE requests stepwise selection. SCORE
requests best subset selection. By default, SELECTION=NONE.
For more information, see the section Effect-Selection Methods.
-
SEQUENTIAL
SEQ
-
forces effects to be added to the model in the order specified in the MODEL statement or eliminated from the model in the
reverse order of that specified in the MODEL statement. The model-building process continues until the next effect to be added
has an insignificant adjusted chi-square statistic or until the next effect to be deleted has a significant Wald chi-square
statistic. The SEQUENTIAL option has no effect when SELECTION=
NONE.
-
SINGULAR=value
-
specifies the tolerance for testing the singularity of the Hessian matrix (Newton-Raphson algorithm) or the expected value
of the Hessian matrix (Fisher scoring algorithm). The Hessian matrix is the matrix of second partial derivatives of the log-likelihood
function. The test requires that a pivot for sweeping this matrix be at least this number times a norm of the matrix. Values
of the SINGULAR= option must be numeric. By default, value is the machine epsilon times 1E7, which is approximately 1E–9.
-
SLENTRY=value
SLE=value
-
specifies the significance level of the score chi-square for entering an effect into the model in the FORWARD or STEPWISE
method. Values of the SLENTRY= option should be between 0 and 1, inclusive. By default, SLENTRY=0.05. The SLENTRY= option
has no effect when SELECTION=
NONE, SELECTION=
BACKWARD, or SELECTION=
SCORE.
-
SLSTAY=value
SLS=value
-
specifies the significance level of the Wald chi-square for an effect to stay in the model in a backward elimination step.
Values of the SLSTAY= option should be between 0 and 1, inclusive. By default, SLSTAY=0.05. The SLSTAY= option has no effect
when SELECTION=
NONE, SELECTION=
FORWARD, or SELECTION=
SCORE.
-
START=number | EQUALSLOPES
-
specifies which effects in the MODEL statement are included in the initial model. You can specify the following values:
- number
-
requests that the first number effects be included in the initial model. The value of number ranges from 0 to s, where s is the total number of effects that are specified in the MODEL statement. The default value of number is s when SELECTION=BACKWARD
and 0 when SELECTION=FORWARD
or SELECTION=STEPWISE
. When SELECTION=SCORE
, START=number specifies that the smallest models contain number effects, where number ranges from 1 to s; the default value is 1.
- EQUALSLOPES
-
enables you to begin the model selection process with all the equal slope effects in the model.
The START= option has no effect when SELECTION=NONE
. You cannot specify the START=EQUALSLOPES option if you specify SELECTION=SCORE
.
If you specify the same effect in both the EQUALSLOPES
and UNEQUALSLOPES
options, then that effect is treated as two separate effects. For example, suppose you specify the following MODEL statement:
model Y=X1 X2 / equalslopes unequalslopes selection=forward;
The X1 and X2 variables both generate an equal slope effect and an unequal slope effect. Specifying START=1 includes the
equal slope effect for X1 in the initial model; specifying START=2 includes both the equal and unequal slope effects for X1
in the initial model; specifying START=EQUALSLOPES includes the equal slope effects for X1 and for X2 in the initial model.
Note that the INCLUDE=
and START= options perform different tasks: the INCLUDE= option includes effects in every model, whereas the START= option
requires only that the effects appear in the first model.
-
STB
-
displays the standardized estimates for the parameters in the "Analysis of Maximum Likelihood Estimates" table. The standardized
estimate of 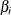 is given by
is given by 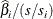 , where
, where  is the total sample standard deviation for the ith explanatory variable and
is the total sample standard deviation for the ith explanatory variable and
The sample standard deviations for parameters associated with CLASS
and EFFECT
variables are computed using their codings. For the intercept parameters, the standardized estimates are set to missing.
-
STOP=number
-
specifies the maximum (SELECTION=
FORWARD) or minimum (SELECTION=
BACKWARD) number of effects to be included in the final model. The effect selection process is stopped when number effects are found. The value of number ranges from 0 to s, where s is the total number of effects in the MODEL statement. The default value of number is s for the FORWARD method and 0 for the BACKWARD method. For the SCORE method, STOP=number specifies that the largest models contain number effects, where number ranges from 1 to s; the default value of number is s. The STOP= option has no effect when SELECTION=
NONE or STEPWISE.
-
STOPRES
SR
-
specifies that the removal or entry of effects be based on the value of the residual chi-square. If SELECTION=
FORWARD, then the STOPRES option adds the effects into the model one at a time until the residual chi-square becomes insignificant
(until the p-value of the residual chi-square exceeds the SLENTRY=
value). If SELECTION=
BACKWARD, then the STOPRES option removes effects from the model one at a time until the residual chi-square becomes significant
(until the p-value of the residual chi-square becomes less than the SLSTAY=
value). The STOPRES option has no effect when SELECTION=
NONE or SELECTION=
STEPWISE.
-
TECHNIQUE=FISHER | NEWTON
TECH=FISHER | NEWTON
-
specifies the optimization technique for estimating the regression parameters. NEWTON (or NR) is the Newton-Raphson algorithm
and FISHER (or FS) is the Fisher scoring algorithm. Both techniques yield the same estimates, but the estimated covariance
matrices are slightly different except for the case when the LOGIT link is specified for binary response data. By default,
TECHNIQUE=FISHER. If you specify the LINK=GLOGIT
or LINK=ALOGIT
option, then Newton-Raphson is the default and only available method. The TECHNIQUE= option is not applied to conditional
and exact conditional analyses. This option is not available when the EQUALSLOPES
or UNEQUALSLOPES
option is specified. For more information, see the section Iterative Algorithms for Model Fitting.
-
UNEQUALSLOPES<=effect>
UNEQUALSLOPES<=(effect-list)>
-
specifies one or more effects in a model for which you want a different set of parameters for each response function. If you
specify more than one effect, enclose the effects in parentheses. The effects must be explanatory effects that are specified
in the MODEL statement. Each member of the effect-list can have one of the following forms:
|
effect
|
|
effect=numberlist
|
|
_C_=numberlist
|
where the numberlist enables you to specify constrained parameters (Peterson and Harrell 1990). To assign a default numberlist for all the explanatory effects in this option, specify the _C_=numberlist form.
For example, suppose your ordinal response variable Y has three levels, {0, 1, 2}, so that you have two cumulative response functions. Let the CLASS variable A have three levels, {a, b, c}, with reference coding. The following table shows how the numberlist is distributed across the models:
|
If You Specify
|
Then You Fit This Model
|
|
unequalslopes=(A=1 2 3 4)
|
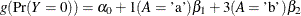
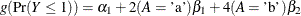
|
|
unequalslopes=(_C_=1 2)
|
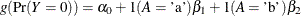
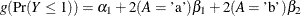
|
If you do not specify this option, the cumulative response models (and the adjacent-category logit model) make the parallel
lines assumption, 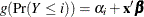 , where each response function has the same slope parameters
, where each response function has the same slope parameters 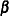 . If you specify this option without an effect or effect-list, all slope parameters vary across the response functions, resulting in the model
. If you specify this option without an effect or effect-list, all slope parameters vary across the response functions, resulting in the model 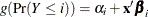 . Specifying an effect or effect-list enables you to choose which effects have different parameters across the response functions, and whether the parameters are
constrained or unconstrained. For any specified selection method, unconstrained parameters can contain and be contained in
only other unconstrained parameters, and constrained parameters can contain and be contained in only other constrained parameters;
for more information, see the HIERARCHY=
option. If you select the first
. Specifying an effect or effect-list enables you to choose which effects have different parameters across the response functions, and whether the parameters are
constrained or unconstrained. For any specified selection method, unconstrained parameters can contain and be contained in
only other unconstrained parameters, and constrained parameters can contain and be contained in only other constrained parameters;
for more information, see the HIERARCHY=
option. If you select the first 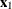 parameters to have equal slopes and the remaining
parameters to have equal slopes and the remaining 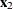 parameters to have unequal slopes, the model can be written as
parameters to have unequal slopes, the model can be written as 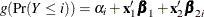 . Such a model that uses the CLOGIT
link is called a partial proportional odds model (Peterson and Harrell 1990).
. Such a model that uses the CLOGIT
link is called a partial proportional odds model (Peterson and Harrell 1990).
You can specify this option along with the EQUALSLOPES
option to create an effect that has both equal and unequal slopes. In this case, the parameters that have equal slopes model
the mean effect across the response functions, whereas the parameters that have unequal slopes model deviations from the mean.
To distinguish between these two types of parameters, the unconstrained unequal slope parameters are prefixed with "U_" and
the constrained parameters are prefixed with "C_". You can use the "Joint Tests" or "Type 3 Analysis of Effects" table to
test whether the unequal slope parameters are zero.
For an example that uses this option, see Example 72.18. If you specify the UNEQUALSLOPES option, you cannot specify any of the EFFECTPLOT, ESTIMATE, EXACT, LSMEANS, LSMESTIMATE,
ROC, ROCCONTRAST, SLICE, STORE, and STRATA statements, and you cannot specify the following options: CTABLE, FIRTH, OUTROC=, PEVENT=, PPROB=, RIDGING=, and TECHNIQUE=.
-
WALDCL
CL
-
is the same as specifying CLPARM=WALD
.
-
XCONV=value
-
specifies the relative parameter convergence criterion. Convergence requires a small relative parameter change in subsequent
iterations,
where
and 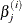 is the estimate of the jth parameter at iteration i. See the section Convergence Criteria for more information.
is the estimate of the jth parameter at iteration i. See the section Convergence Criteria for more information.
 PROC LOGISTIC StatementBY StatementCLASS StatementCODE StatementCONTRAST StatementEFFECT StatementEFFECTPLOT StatementESTIMATE StatementEXACT StatementEXACTOPTIONS StatementFREQ StatementID StatementLSMEANS StatementLSMESTIMATE StatementMODEL StatementNLOPTIONS StatementODDSRATIO StatementOUTPUT StatementROC StatementROCCONTRAST StatementSCORE StatementSLICE StatementSTORE StatementSTRATA StatementTEST StatementUNITS StatementWEIGHT Statement
PROC LOGISTIC StatementBY StatementCLASS StatementCODE StatementCONTRAST StatementEFFECT StatementEFFECTPLOT StatementESTIMATE StatementEXACT StatementEXACTOPTIONS StatementFREQ StatementID StatementLSMEANS StatementLSMESTIMATE StatementMODEL StatementNLOPTIONS StatementODDSRATIO StatementOUTPUT StatementROC StatementROCCONTRAST StatementSCORE StatementSLICE StatementSTORE StatementSTRATA StatementTEST StatementUNITS StatementWEIGHT Statement Missing ValuesResponse Level OrderingLink Functions and the Corresponding DistributionsDetermining Observations for Likelihood ContributionsIterative Algorithms for Model FittingConvergence CriteriaExistence of Maximum Likelihood EstimatesEffect-Selection MethodsModel Fitting InformationGeneralized Coefficient of DeterminationScore Statistics and TestsConfidence Intervals for ParametersOdds Ratio EstimationRank Correlation of Observed Responses and Predicted ProbabilitiesLinear Predictor, Predicted Probability, and Confidence LimitsClassification TableOverdispersionThe Hosmer-Lemeshow Goodness-of-Fit TestReceiver Operating Characteristic CurvesTesting Linear Hypotheses about the Regression CoefficientsJoint Tests and Type 3 TestsRegression DiagnosticsScoring Data SetsConditional Logistic RegressionExact Conditional Logistic RegressionInput and Output Data SetsComputational ResourcesDisplayed OutputODS Table NamesODS Graphics
Missing ValuesResponse Level OrderingLink Functions and the Corresponding DistributionsDetermining Observations for Likelihood ContributionsIterative Algorithms for Model FittingConvergence CriteriaExistence of Maximum Likelihood EstimatesEffect-Selection MethodsModel Fitting InformationGeneralized Coefficient of DeterminationScore Statistics and TestsConfidence Intervals for ParametersOdds Ratio EstimationRank Correlation of Observed Responses and Predicted ProbabilitiesLinear Predictor, Predicted Probability, and Confidence LimitsClassification TableOverdispersionThe Hosmer-Lemeshow Goodness-of-Fit TestReceiver Operating Characteristic CurvesTesting Linear Hypotheses about the Regression CoefficientsJoint Tests and Type 3 TestsRegression DiagnosticsScoring Data SetsConditional Logistic RegressionExact Conditional Logistic RegressionInput and Output Data SetsComputational ResourcesDisplayed OutputODS Table NamesODS Graphics Stepwise Logistic Regression and Predicted ValuesLogistic Modeling with Categorical PredictorsOrdinal Logistic RegressionNominal Response Data: Generalized Logits ModelStratified SamplingLogistic Regression DiagnosticsROC Curve, Customized Odds Ratios, Goodness-of-Fit Statistics, R-Square, and Confidence LimitsComparing Receiver Operating Characteristic CurvesGoodness-of-Fit Tests and SubpopulationsOverdispersionConditional Logistic Regression for Matched Pairs DataExact Conditional Logistic RegressionFirth’s Penalized Likelihood Compared with Other ApproachesComplementary Log-Log Model for Infection RatesComplementary Log-Log Model for Interval-Censored Survival TimesScoring Data SetsUsing the LSMEANS StatementPartial Proportional Odds Model
Stepwise Logistic Regression and Predicted ValuesLogistic Modeling with Categorical PredictorsOrdinal Logistic RegressionNominal Response Data: Generalized Logits ModelStratified SamplingLogistic Regression DiagnosticsROC Curve, Customized Odds Ratios, Goodness-of-Fit Statistics, R-Square, and Confidence LimitsComparing Receiver Operating Characteristic CurvesGoodness-of-Fit Tests and SubpopulationsOverdispersionConditional Logistic Regression for Matched Pairs DataExact Conditional Logistic RegressionFirth’s Penalized Likelihood Compared with Other ApproachesComplementary Log-Log Model for Infection RatesComplementary Log-Log Model for Interval-Censored Survival TimesScoring Data SetsUsing the LSMEANS StatementPartial Proportional Odds Model
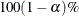
![\[ |l_ i - l_{i-1}| < \mi{value} \]](images/statug_logistic0076.png)
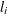
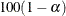
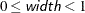
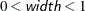
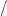
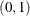
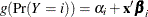
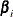
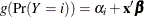
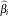
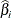
![\[ \frac{ |l_ i - l_{i-1}|}{|l_{i-1}| + {\mbox{1E--6}}} < \mi{value} \]](images/statug_logistic0079.png)
![\[ \frac{\mb{g}_ i^{\prime } \bI _ i^{-1} \mb{g}_ i}{|l_ i| + {\mbox{1E--6}}} < \mi{value} \]](images/statug_logistic0096.png)
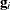
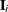
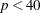
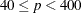
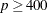
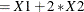
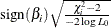
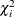
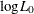
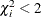
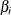
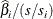

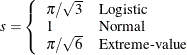
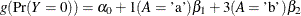
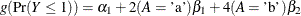
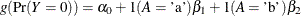
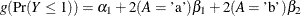
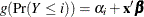
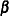
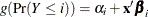
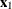
![\[ \max _ j |\delta _ j^{(i)}| < \mi{value} \]](images/statug_logistic0082.png)