The LOGISTIC Procedure
- Overview
- Getting Started
-
Syntax
 PROC LOGISTIC StatementBY StatementCLASS StatementCODE StatementCONTRAST StatementEFFECT StatementEFFECTPLOT StatementESTIMATE StatementEXACT StatementEXACTOPTIONS StatementFREQ StatementID StatementLSMEANS StatementLSMESTIMATE StatementMODEL StatementNLOPTIONS StatementODDSRATIO StatementOUTPUT StatementROC StatementROCCONTRAST StatementSCORE StatementSLICE StatementSTORE StatementSTRATA StatementTEST StatementUNITS StatementWEIGHT Statement
PROC LOGISTIC StatementBY StatementCLASS StatementCODE StatementCONTRAST StatementEFFECT StatementEFFECTPLOT StatementESTIMATE StatementEXACT StatementEXACTOPTIONS StatementFREQ StatementID StatementLSMEANS StatementLSMESTIMATE StatementMODEL StatementNLOPTIONS StatementODDSRATIO StatementOUTPUT StatementROC StatementROCCONTRAST StatementSCORE StatementSLICE StatementSTORE StatementSTRATA StatementTEST StatementUNITS StatementWEIGHT Statement -
Details
 Missing ValuesResponse Level OrderingLink Functions and the Corresponding DistributionsDetermining Observations for Likelihood ContributionsIterative Algorithms for Model FittingConvergence CriteriaExistence of Maximum Likelihood EstimatesEffect-Selection MethodsModel Fitting InformationGeneralized Coefficient of DeterminationScore Statistics and TestsConfidence Intervals for ParametersOdds Ratio EstimationRank Correlation of Observed Responses and Predicted ProbabilitiesLinear Predictor, Predicted Probability, and Confidence LimitsClassification TableOverdispersionThe Hosmer-Lemeshow Goodness-of-Fit TestReceiver Operating Characteristic CurvesTesting Linear Hypotheses about the Regression CoefficientsJoint Tests and Type 3 TestsRegression DiagnosticsScoring Data SetsConditional Logistic RegressionExact Conditional Logistic RegressionInput and Output Data SetsComputational ResourcesDisplayed OutputODS Table NamesODS Graphics
Missing ValuesResponse Level OrderingLink Functions and the Corresponding DistributionsDetermining Observations for Likelihood ContributionsIterative Algorithms for Model FittingConvergence CriteriaExistence of Maximum Likelihood EstimatesEffect-Selection MethodsModel Fitting InformationGeneralized Coefficient of DeterminationScore Statistics and TestsConfidence Intervals for ParametersOdds Ratio EstimationRank Correlation of Observed Responses and Predicted ProbabilitiesLinear Predictor, Predicted Probability, and Confidence LimitsClassification TableOverdispersionThe Hosmer-Lemeshow Goodness-of-Fit TestReceiver Operating Characteristic CurvesTesting Linear Hypotheses about the Regression CoefficientsJoint Tests and Type 3 TestsRegression DiagnosticsScoring Data SetsConditional Logistic RegressionExact Conditional Logistic RegressionInput and Output Data SetsComputational ResourcesDisplayed OutputODS Table NamesODS Graphics -
Examples
 Stepwise Logistic Regression and Predicted ValuesLogistic Modeling with Categorical PredictorsOrdinal Logistic RegressionNominal Response Data: Generalized Logits ModelStratified SamplingLogistic Regression DiagnosticsROC Curve, Customized Odds Ratios, Goodness-of-Fit Statistics, R-Square, and Confidence LimitsComparing Receiver Operating Characteristic CurvesGoodness-of-Fit Tests and SubpopulationsOverdispersionConditional Logistic Regression for Matched Pairs DataExact Conditional Logistic RegressionFirth’s Penalized Likelihood Compared with Other ApproachesComplementary Log-Log Model for Infection RatesComplementary Log-Log Model for Interval-Censored Survival TimesScoring Data SetsUsing the LSMEANS StatementPartial Proportional Odds Model
Stepwise Logistic Regression and Predicted ValuesLogistic Modeling with Categorical PredictorsOrdinal Logistic RegressionNominal Response Data: Generalized Logits ModelStratified SamplingLogistic Regression DiagnosticsROC Curve, Customized Odds Ratios, Goodness-of-Fit Statistics, R-Square, and Confidence LimitsComparing Receiver Operating Characteristic CurvesGoodness-of-Fit Tests and SubpopulationsOverdispersionConditional Logistic Regression for Matched Pairs DataExact Conditional Logistic RegressionFirth’s Penalized Likelihood Compared with Other ApproachesComplementary Log-Log Model for Infection RatesComplementary Log-Log Model for Interval-Censored Survival TimesScoring Data SetsUsing the LSMEANS StatementPartial Proportional Odds Model - References
Example 72.14 Complementary Log-Log Model for Infection Rates
Antibodies produced in response to an infectious disease like malaria remain in the body after the individual has recovered
from the disease. A serological test detects the presence or absence of such antibodies. An individual with such antibodies
is called seropositive. In geographic areas where the disease is endemic, the inhabitants are at fairly constant risk of infection.
The probability of an individual never having been infected in Y years is 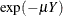 , where
, where 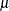 is the mean number of infections per year (see the appendix of Draper, Voller, and Carpenter 1972). Rather than estimating the unknown
is the mean number of infections per year (see the appendix of Draper, Voller, and Carpenter 1972). Rather than estimating the unknown 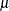 , epidemiologists want to estimate the probability of a person living in the area being infected in one year. This infection
rate
, epidemiologists want to estimate the probability of a person living in the area being infected in one year. This infection
rate 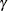 is given by
is given by
![\[ \gamma = 1-{e}^{-\mu } \]](images/statug_logistic0801.png)
The following statements create the data set sero, which contains the results of a serological survey of malarial infection. Individuals of nine age groups (Group) were tested. The variable A represents the midpoint of the age range for each age group. The variable N represents the number of individuals tested in each age group, and the variable R represents the number of individuals that are seropositive.
data sero; input Group A N R; X=log(A); label X='Log of Midpoint of Age Range'; datalines; 1 1.5 123 8 2 4.0 132 6 3 7.5 182 18 4 12.5 140 14 5 17.5 138 20 6 25.0 161 39 7 35.0 133 19 8 47.0 92 25 9 60.0 74 44 ;
For the ith group with the age midpoint 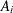 , the probability of being seropositive is
, the probability of being seropositive is 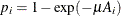 . It follows that
. It follows that
![\[ \log (-\log (1-p_ i)) = \log (\mu ) + \log (A_ i) \]](images/statug_logistic0804.png)
By fitting a binomial model with a complementary log-log link function and by using X=log(A) as an offset term, you can estimate
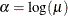 as an intercept parameter. The following statements invoke PROC LOGISTIC to compute the maximum likelihood estimate of
as an intercept parameter. The following statements invoke PROC LOGISTIC to compute the maximum likelihood estimate of  . The LINK=CLOGLOG
option is specified to request the complementary log-log link function. Also specified is the CLPARM=PL
option, which requests the profile-likelihood confidence limits for
. The LINK=CLOGLOG
option is specified to request the complementary log-log link function. Also specified is the CLPARM=PL
option, which requests the profile-likelihood confidence limits for  .
.
proc logistic data=sero;
model R/N= / offset=X
link=cloglog
clparm=pl
scale=none;
title 'Constant Risk of Infection';
run;
Results of fitting this constant risk model are shown in Output 72.14.1.
Output 72.14.1: Modeling Constant Risk of Infection
Output 72.14.1 shows that the maximum likelihood estimate of 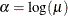 and its estimated standard error are
and its estimated standard error are 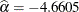 and
and 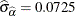 , respectively. The infection rate is estimated as
, respectively. The infection rate is estimated as
![\[ \widehat{\gamma }=1-{e}^{-\widehat{\mu }} =1-{e}^{-{e}^{{\widehat{\beta }}_0}} =1-{e}^{-{e}^{-4.6605}} =0.00942 \]](images/statug_logistic0808.png)
The 95% confidence interval for 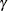 , obtained by back-transforming the 95% confidence interval for
, obtained by back-transforming the 95% confidence interval for  , is (0.0082, 0.0108); that is, there is a 95% chance that, in repeated sampling, the interval of 8 to 11 infections per thousand
individuals contains the true infection rate.
, is (0.0082, 0.0108); that is, there is a 95% chance that, in repeated sampling, the interval of 8 to 11 infections per thousand
individuals contains the true infection rate.
The goodness-of-fit statistics for the constant risk model are statistically significant (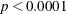 ), indicating that the assumption of constant risk of infection is not correct. You can fit a more extensive model by allowing
a separate risk of infection for each age group. Suppose
), indicating that the assumption of constant risk of infection is not correct. You can fit a more extensive model by allowing
a separate risk of infection for each age group. Suppose 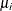 is the mean number of infections per year for the ith age group. The probability of seropositive for the ith group with the age midpoint
is the mean number of infections per year for the ith age group. The probability of seropositive for the ith group with the age midpoint 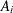 is
is 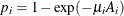 , so that
, so that
![\[ \log (-\log (1-p_ i))=\log (\mu _ i) + \log (A_ i) \]](images/statug_logistic0811.png)
In the following statements, a complementary log-log model is fit containing Group as an explanatory classification variable with the GLM coding (so that a dummy variable is created for each age group), no
intercept term, and X=log(A) as an offset term. The ODS OUTPUT statement saves the estimates and their 95% profile-likelihood
confidence limits to the ClparmPL data set. Note that 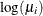 is the regression parameter associated with
is the regression parameter associated with Group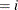 .
.
proc logistic data=sero;
ods output ClparmPL=ClparmPL;
class Group / param=glm;
model R/N=Group / noint
offset=X
link=cloglog
clparm=pl;
title 'Infectious Rates and 95% Confidence Intervals';
run;
Results of fitting the model with a separate risk of infection are shown in Output 72.14.2.
Output 72.14.2: Modeling Separate Risk of Infection
| Infectious Rates and 95% Confidence Intervals |
| Analysis of Maximum Likelihood Estimates | ||||||
|---|---|---|---|---|---|---|
| Parameter | DF | Estimate | Standard Error |
Wald Chi-Square |
Pr > ChiSq | |
| Group | 1 | 1 | -3.1048 | 0.3536 | 77.0877 | <.0001 |
| Group | 2 | 1 | -4.4542 | 0.4083 | 119.0164 | <.0001 |
| Group | 3 | 1 | -4.2769 | 0.2358 | 328.9593 | <.0001 |
| Group | 4 | 1 | -4.7761 | 0.2674 | 319.0600 | <.0001 |
| Group | 5 | 1 | -4.7165 | 0.2238 | 443.9920 | <.0001 |
| Group | 6 | 1 | -4.5012 | 0.1606 | 785.1350 | <.0001 |
| Group | 7 | 1 | -5.4252 | 0.2296 | 558.1114 | <.0001 |
| Group | 8 | 1 | -4.9987 | 0.2008 | 619.4666 | <.0001 |
| Group | 9 | 1 | -4.1965 | 0.1559 | 724.3157 | <.0001 |
| X | 0 | 1.0000 | 0 | . | . | |
| Parameter Estimates and Profile-Likelihood Confidence Intervals |
||||
|---|---|---|---|---|
| Parameter | Estimate | 95% Confidence Limits | ||
| Group | 1 | -3.1048 | -3.8880 | -2.4833 |
| Group | 2 | -4.4542 | -5.3769 | -3.7478 |
| Group | 3 | -4.2769 | -4.7775 | -3.8477 |
| Group | 4 | -4.7761 | -5.3501 | -4.2940 |
| Group | 5 | -4.7165 | -5.1896 | -4.3075 |
| Group | 6 | -4.5012 | -4.8333 | -4.2019 |
| Group | 7 | -5.4252 | -5.9116 | -5.0063 |
| Group | 8 | -4.9987 | -5.4195 | -4.6289 |
| Group | 9 | -4.1965 | -4.5164 | -3.9037 |
For the first age group (Group=1), the point estimate of 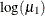 is –3.1048, which transforms into an infection rate of
is –3.1048, which transforms into an infection rate of 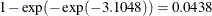 . A 95% confidence interval for this infection rate is obtained by transforming the 95% confidence interval for
. A 95% confidence interval for this infection rate is obtained by transforming the 95% confidence interval for 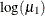 . For the first age group, the lower and upper confidence limits are
. For the first age group, the lower and upper confidence limits are 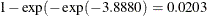 and
and 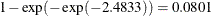 , respectively; that is, there is a 95% chance that, in repeated sampling, the interval of 20 to 80 infections per thousand
individuals contains the true infection rate. The following statements perform this transformation on the estimates and confidence
limits saved in the
, respectively; that is, there is a 95% chance that, in repeated sampling, the interval of 20 to 80 infections per thousand
individuals contains the true infection rate. The following statements perform this transformation on the estimates and confidence
limits saved in the ClparmPL data set; the resulting estimated infection rates in one year’s time for each age group are displayed in Table 72.18. Note that the infection rate for the first age group is high compared to that of the other age groups.
data ClparmPL; set ClparmPL; Estimate=round( 1000*( 1-exp(-exp(Estimate)) ) ); LowerCL =round( 1000*( 1-exp(-exp(LowerCL )) ) ); UpperCL =round( 1000*( 1-exp(-exp(UpperCL )) ) ); run;
Table 72.18: Infection Rate in One Year
|
Number Infected per 1,000 People |
|||
|---|---|---|---|
|
Age |
Point |
95% Confidence Limits |
|
|
Group |
Estimate |
Lower |
Upper |
|
1 |
44 |
20 |
80 |
|
2 |
12 |
5 |
23 |
|
3 |
14 |
8 |
21 |
|
4 |
8 |
5 |
14 |
|
5 |
9 |
6 |
13 |
|
6 |
11 |
8 |
15 |
|
7 |
4 |
3 |
7 |
|
8 |
7 |
4 |
10 |
|
9 |
15 |
11 |
20 |