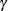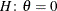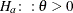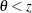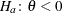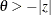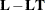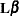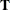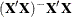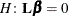-
ADJDFE=SOURCE
ADJDFE=ROW
-
specifies how denominator degrees of freedom are determined when
p-values and confidence limits are adjusted for multiple comparisons with the ADJUST=
option. When you do not specify the ADJDFE= option, or when you specify ADJDFE=SOURCE, the denominator degrees of freedom
for multiplicity-adjusted results are the denominator degrees of freedom for the final effect that is listed in the ESTIMATE
statement from the "Type III" table.
The ADJDFE=ROW setting is useful if you want multiplicity adjustments to take into account that denominator degrees of freedom
are not constant across estimates. For example, this can be the case when the denominator degrees of freedom are computed
by the Satterthwaite method or according to Kenward and Roger (1997).
The ADJDFE= option has an effect only in mixed models that use these degree-of-freedom methods. It is not supported by the
procedures that perform chi-square-based inference (LOGISTIC, PHREG, and SURVEYLOGISTIC).
-
ADJUST=BON
ADJUST=SCHEFFE
ADJUST=SIDAK
ADJUST=SIMULATE<(sim-options)>
ADJUST=T
-
requests a multiple comparison adjustment for the p-values and
confidence limits for the estimates. The adjusted quantities are produced in addition to the unadjusted quantities. Adjusted
confidence limits are produced if the CL
or ALPHA=
option is in effect. For a description of the adjustments, see Chapter 46: The GLM Procedure, and Chapter 79: The MULTTEST Procedure, and the documentation for the ADJUST=
option in the LSMEANS
statement.
If the STEPDOWN
option is in effect, the p-values are further adjusted in a step-down fashion.
-
ALPHA=number
-
requests that a t type confidence interval be constructed
with confidence level 1 – number. The value of number must be between 0 and 1; the default is 0.05. If the "Estimates" table shows infinite degrees of freedom, then the confidence
interval is a z type interval.
-
CATEGORY=category-options
-
specifies how to construct estimates and multiplicity corrections for
models with multinomial data (ordinal or nominal). This option is also important for constructing sets of estimable functions
for F or chi-square tests with the JOINT
option.
The category-options are used to indicate how response variable levels are treated in constructing the estimable functions. Possible values for
the category-options are the following:
-
JOINT
-
computes the estimable functions for every nonredundant category and treats them as a set. For example, a three-row ESTIMATE
statement in a model with three response categories leads to six estimable functions.
-
SEPARATE
-
computes the estimable functions for every nonredundant category in turn. For example, a three-row ESTIMATE statement in a
model with three response categories leads to two sets of three estimable functions.
-
quoted-value-list
-
computes the estimable functions only for the specified list of values. The list must consist of formatted values of the response
categories, and you must specify an estimate-specification for each response category in the list.
Consider the following ESTIMATE statements in the LOGISTIC procedure for an ordinal model with response categories 'vg', 'g',
'm', 'b', and 'vb'. Because there are five response categories, there are four nonredundant categories for the cumulative
link model.
proc logistic data=icecream;
class brand / param=glm;
model taste(order=data) = brand / link=logit;
freq count;
estimate brand 1 -1,
intercept 1 brand 0 1 / category='m','vg';
estimate intercept 1 brand 1 / category=joint
adjust=simulate(seed=1);
estimate brand 1 -1,
brand 1 1 -2 / category=separate
adjust=bon;
run;
The first ESTIMATE statement requests a two-row estimable function. The result is produced for two of the four nonredundant
response categories. The second ESTIMATE statement produces four t tests, one for each nonredundant category. The multiplicity adjustment with p-value computation by simulation treats the four estimable functions as a unit for family-wise Type I error protection. The
third ESTIMATE statement computes a two-row estimable function and reports its results separately for all nonredundant categories.
The Bonferroni adjustment in this statement applies to a family of two tests that correspond to the two-row estimable function.
Four Bonferroni adjustments for sets of size two are performed.
The CATEGORY= option is supported only by the procedures that support generalized linear modeling (GEE, LOGISTIC, and SURVEYLOGISTIC)
and by PROC PLM when it is used to perform statistical analyses on item stores created by these procedures.
-
CHISQ
-
requests that chi-square tests be performed in addition to
F tests, when you request an F test with the JOINT
option. This option has no effect in procedures that produce chi-square statistics by default.
-
CL
-
requests that t type confidence limits be constructed.
If the procedure shows the degrees of freedom in the "Estimates" table as infinite, then the confidence limits are z intervals. The confidence level is 0.95 by default, and you can change the confidence level with the ALPHA=
option. The confidence intervals are adjusted for multiplicity when you specify the ADJUST= option. However, if a step-down
p-value adjustment is requested with the STEPDOWN
option, only the p-values are adjusted for multiplicity.
-
CORR
-
displays the estimated correlation matrix of the linear combination of
the parameter estimates.
-
COV
-
displays the estimated covariance matrix of the linear combination of
the parameter estimates.
-
DF=number
-
specifies the degrees of freedom for the t test and confidence
limits. This option is not supported by the procedures that perform chi-square-based inference (LOGISTIC, PHREG, and SUVEYLOGISTIC).
-
DIVISOR=value-list
-
specifies a list of values by which to divide the coefficients so that
fractional coefficients can be entered as integer numerators. If you do not specify value-list, a default value of 1.0 is assumed. Missing values in the value-list are converted to 1.0.
If the number of elements in value-list exceeds the number of rows of the estimate, the extra values are ignored. If the number of elements in value-list is less than the number of rows of the estimate, the last value in value-list is copied forward.
If you specify a row-specific divisor as part of the specification of the estimate row, this value multiplies the corresponding
divisor that is implied by the value-list. For example, the following statement divides the coefficients in the first row by 8, and the coefficients in the third and
fourth row by 3:
estimate 'One vs. two' A 2 -2 (divisor=2),
'One vs. three' A 1 0 -1 ,
'One vs. four' A 3 0 0 -3 ,
'One vs. five' A 1 0 0 0 -1 / divisor=4,.,3;
Coefficients in the second row are not altered.
-
E
-
requests that the  matrix coefficients be displayed.
matrix coefficients be displayed.
-
EXP
-
requests exponentiation of the estimate.
When you model data with the logit, cumulative logit, or generalized logit link functions, and the estimate represents a log
odds ratio or log cumulative odds ratio, the EXP option produces an odds ratio. In proportional hazards model, this option
produces estimates of hazard ratios. If you specify the CL
or ALPHA=
option, the (adjusted) confidence bounds are also exponentiated.
The EXP option is supported only by PROC PHREG, PROC SURVEYPHREG, the procedures that support generalized linear modeling
(LOGISTIC and SURVEYLOGISTIC), and by PROC PLM when it is used to perform statistical analyses on item stores created by these
procedures.
-
ILINK
-
requests that the estimate and its standard error also be reported
on the scale of the mean (the inverse linked scale). The computation of the inverse linked estimate depends on the estimation
mode. For example, if the analysis is based on a posterior sample when a BAYES statement is present, the inversely linked
estimate is the average of the inversely linked values across the sample of posterior parameter estimates. If the analysis
is not based on a sample of parameter estimates, the procedure computes the value on the mean scale by applying the inverse
link to the estimate. The interpretation of this quantity depends on the effect values specified in your ESTIMATE statement and on the link function. For example, in a model for binary data with logit link the
following statements compute
where 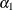 and
and 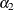 are the fixed-effects solutions that are associated with the first two levels of the classification effect
are the fixed-effects solutions that are associated with the first two levels of the classification effect A:
class A;
model y = A / dist=binary link=logit;
estimate 'A one vs. two' A 1 -1 / ilink;
This quantity is not the difference of the probabilities that are associated with the two levels,
The standard error of the inversely linked estimate is based on the delta method. If you also specify the CL
option, the procedure computes confidence limits for the estimate on the mean scale. In multinomial models for nominal data,
the limits are obtained by the delta method. In other models they are obtained from the inverse link transformation of the
confidence limits for the estimate. The ILINK option is specific to an ESTIMATE statement.
The ILINK option is supported only by the procedures that support generalized linear modeling (LOGISTIC and SURVEYLOGISTIC)
and by PROC PLM when it is used to perform statistical analyses on item stores created by these procedures.
-
JOINT<(joint-test-options)>
-
requests that a joint F or chi-square test be produced for the
rows of the estimate. The JOINT option in the ESTIMATE statement essentially replaces the CONTRAST statement.
When the LOWERTAILED
or the UPPERTAILED
options are in effect, or if the BOUNDS option described below is in effect, the JOINT option produces the chi-bar-square
statistic according to Silvapulle and Sen (2004). This statistic uses a simulation-based approach to compute p-values in situations where the alternative hypotheses of the estimable functions are not simple two-sided hypotheses. See
the section Joint Hypothesis Tests with Complex Alternatives, the Chi-Bar-Square Statistic for more information about this test statistic.
You can specify the following joint-test-options in parentheses:
-
ACC=
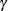
-
specifies the accuracy radius for determining the necessary sample size in the simulation-based approach of Silvapulle and
Sen (2004) for tests with order restrictions. The value of 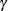 must be strictly between 0 and 1; the default value is 0.005.
must be strictly between 0 and 1; the default value is 0.005.
-
EPS=

-
specifies the accuracy confidence level for determining the necessary sample size in the simulation-based approach of Silvapulle
and Sen (2004) for tests with order restrictions. The value of  must be strictly between 0 and 1; the default value is 0.01.
must be strictly between 0 and 1; the default value is 0.01.
-
LABEL='label'
-
assigns an identifying label to the joint test. If you do not specify a label, the first non-default label for the ESTIMATE
rows is used to label the joint test.
-
NOEST
ONLY
-
performs only the F or chi-square test and suppresses other results from the ESTIMATE statement. This option is useful for emulating the CONTRAST
statement that is available in other procedures.
-
NSAMP=n
-
specifies the number of samples for the simulation-based method of Silvapulle and Sen (2004). If n is not specified, it is constructed from the values of the ALPHA= , the ACC=
, the ACC=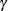 , and the EPS=
, and the EPS= options. With the default values for
options. With the default values for 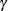 ,
,  , and
, and  (0.005, 0.01, and 0.05, respectively), NSAMP=12,604 by default.
(0.005, 0.01, and 0.05, respectively), NSAMP=12,604 by default.
-
CHISQ
-
adds a chi-square test if the procedure produces an F test by default.
-
BOUNDS=value-list
-
specifies boundary values for the estimable linear function. The null value of the hypothesis is always zero. If you specify
a positive boundary value z, the hypotheses are 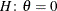 ,
, 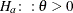 with the added constraint that
with the added constraint that 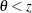 . The same is true for negative boundary values. The alternative hypothesis is then
. The same is true for negative boundary values. The alternative hypothesis is then 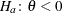 subject to the constraint
subject to the constraint 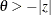 . If you specify a missing value, the hypothesis is assumed to be two-sided. The BOUNDS option enables you to specify sets
of one- and two-sided joint hypotheses. If all values in value-list are set to missing, the procedure performs a simulation-based p-value calculation for a two-sided test.
. If you specify a missing value, the hypothesis is assumed to be two-sided. The BOUNDS option enables you to specify sets
of one- and two-sided joint hypotheses. If all values in value-list are set to missing, the procedure performs a simulation-based p-value calculation for a two-sided test.
-
LOWER
LOWERTAILED
-
requests that the p-value for the t test be based
only on values that are less than the test statistic. A two-tailed test is the default. A lower-tailed confidence limit is
also produced if you specify the CL
or ALPHA=
option.
Note that for ADJUST=
SCHEFFE the one-sided adjusted confidence intervals and one-sided adjusted p-values are the same as the corresponding two-sided statistics, because this adjustment is based on only the right tail of
the F distribution.
If you request a joint test with the JOINT
option, then a one-sided left-tailed order restriction is applied to all estimable functions, and the corresponding chi-bar-square
statistic of Silvapulle and Sen (2004) is computed in addition to the two-sided, standard, F or chi-square statistic. See the JOINT
option for how to control the computation of the simulation-based chi-bar-square statistic.
-
NOFILL
-
suppresses the automatic fill-in of coefficients of higher-order
effects.
-
PLOTS=plot-options
-
produces ODS statistical graphics of the distribution of estimable
functions if the procedure performs the analysis in a sampling-based mode. For example, this is the case when procedures support
a BAYES statement and perform a Bayesian analysis. The estimable functions are then computed for each of the posterior parameter
estimates, and the "Estimates" table reports simple descriptive statistics for the evaluated functions. The PLOTS= option
enables you in this situation to visualize the distribution of the estimable function. The following plot-options are available:
-
ALL
-
produces all possible plots with their default settings.
-
BOXPLOT<(boxplot-options)>
-
produces box plots of the distribution of the estimable function across the posterior sample. A separate box is generated
for each estimable function, and all boxes appear on a single graph by default. You can affect the appearance of the box plot
graph with the following options:
-
ORIENTATION=VERTICAL | HORIZONTAL
ORIENT=VERT | HORIZ
-
specifies the orientation of the boxes. The default is vertical orientation of the box plots.
-
NPANELPOS=number
-
specifies how to break the series of box plots across multiple panels. If the NPANELPOS option is not specified, or if number equals zero, then all box plots are displayed in a single graph; this is the default. If a negative number is specified,
then exactly up to 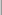 number
number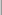 of box plots are displayed per panel. If number is positive, then the number of boxes per panel is balanced to achieve small variation in the number of box plots per graph.
of box plots are displayed per panel. If number is positive, then the number of boxes per panel is balanced to achieve small variation in the number of box plots per graph.
-
DISTPLOT<(distplot-options)>
DIST<(distplot-options)>
-
generates panels of histograms with a kernel density overlaid. A separate plot in each panel contains the results for each
estimable function. You can specify the following distplot-options in parentheses:
-
BOX | NOBOX
-
controls the display of a horizontal box plot of the estimable function’s distribution across the posterior sample below the
graph. The BOX option is enabled by default.
-
HIST | NOHIST
-
controls the display of the histogram of the estimable function’s distribution across the posterior sample. The HIST option
is enabled by default.
-
NORMAL | NONORMAL
-
controls the display of a normal density estimate on the graph. The NONORMAL option is enabled by default.
-
KERNEL | NOKERNEL
-
controls the display of a kernel density estimate on the graph. The KERNEL option is enabled by default.
-
NROWS=number
-
specifies the highest number of rows in a panel. The default is 3.
-
NCOLS=number
-
specifies the highest number of columns in a panel. The default is 3.
-
UNPACK
-
unpacks the panel into separate graphics.
-
NONE
-
does not produce any plots.
-
SEED=number
-
specifies the seed for the sampling-based components of the
computations for the ESTIMATE statement (for example, chi-bar-square statistics and simulated p-values). The value of number must be an integer. The seed is used to start the pseudo-random number generator for the simulation. If you do not specify
a seed, or if you specify a value less than or equal to zero, the seed is generated from reading the time of day from the
computer clock. There could be multiple ESTIMATE statements with SEED= specifications and there could be other statements
that can supply a random number seed. Since the procedure has only one random number stream, the initial seed is shown in
the SAS log.
-
SINGULAR=number
-
tunes the estimability checking. If  is a vector, define
ABS(
is a vector, define
ABS( ) to be the largest absolute value of the elements of
) to be the largest absolute value of the elements of  . If ABS(
. If ABS(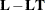 ) is greater than c*number for any row of
) is greater than c*number for any row of  in the contrast, then
in the contrast, then 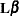 is declared nonestimable. Here,
is declared nonestimable. Here, 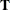 is the Hermite form matrix
is the Hermite form matrix 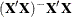 , and c is ABS(
, and c is ABS( ), except when it equals 0, and then c is 1. The value for number must be between 0 and 1; the default is 1E–4.
), except when it equals 0, and then c is 1. The value for number must be between 0 and 1; the default is 1E–4.
-
STEPDOWN<(step-down-options)>
-
requests that multiplicity adjustments for the
p-values of estimates be further adjusted in a step-down fashion. Step-down methods increase the power of multiple testing
procedures by taking advantage of the fact that a p-value is never declared significant unless all smaller p-values are also declared significant. The STEPDOWN adjustment combined with ADJUST=
BON corresponds to the methods of Holm (1979) and "Method 2" of Shaffer (1986); this is the default. Using step-down-adjusted p-values combined with ADJUST=
SIMULATE corresponds to the method of Westfall (1997).
If the ESTIMATE statement is applied with a STEPDOWN option in a mixed model where the degrees-of-freedom method is that of
Kenward and Roger (1997) or of Satterthwaite, then step-down-adjusted p-values are produced only if the ADJDFE
=ROW option is in effect.
Also, the STEPDOWN option affects only p-values, not confidence limits. For ADJUST=
SIMULATE, the generalized least squares hybrid approach of Westfall (1997) is used to increase Monte Carlo accuracy. You can specify the following step-down-options in parentheses after the STEPDOWN option:
-
MAXTIME=n
-
specifies the time (in seconds) to be spent computing the maximal logically consistent sequential subsets of equality hypotheses
for TYPE=LOGICAL. The default is MAXTIME=60. If the MAXTIME value is exceeded, the adjusted tests are not computed. When this
occurs, you can try increasing the MAXTIME value. However, note that there are common multiple comparisons problems for which
this computation requires a huge amount of time—for example, all pairwise comparisons between more than 10 groups. In such
cases, try to use TYPE=FREE (the default) or TYPE=LOGICAL(n) for small n.
-
ORDER=PVALUE
ORDER=ROWS
-
specifies the order in which the step-down tests to be performed. ORDER=PVALUE is the default, with estimates being declared
significant only if all estimates with smaller (unadjusted) p-values are significant. If you specify ORDER=ROWS, then significances are evaluated in the order in which they are specified
in the syntax.
-
REPORT
-
specifies that a report on the step-down adjustment be displayed, including a listing of the sequential subsets (Westfall
1997) and, for ADJUST=
SIMULATE, the step-down simulation results.
-
TYPE=LOGICAL<(n)>
TYPE=FREE
-
specifies how step-down adjustment are made. If you specify TYPE=LOGICAL, the step-down adjustments are computed by using
maximal logically consistent sequential subsets of equality hypotheses (Shaffer 1986; Westfall 1997). Alternatively, for TYPE=FREE, sequential subsets are computed ignoring logical constraints. The TYPE=FREE results are more
conservative than those for TYPE=LOGICAL, but they can be much more efficient to produce for many estimates. For example,
it is not feasible to take logical constraints between all pairwise comparisons of more than about 10 groups. For this reason,
TYPE=FREE is the default.
However, you can reduce the computational complexity of taking logical constraints into account by limiting the depth of the
search tree used to compute them, specifying the optional depth parameter as a number n in parentheses after TYPE=LOGICAL. As with TYPE=FREE, results for TYPE=LOGICAL(n) are conservative relative to the true TYPE=LOGICAL results. But even for TYPE=LOGICAL(0) they can be appreciably less conservative
than TYPE=FREE, and they are computationally feasible for much larger numbers of estimates. If you do not specify n or if n = –1, the full search tree is used.
-
TESTVALUE=value-list
TESTMEAN=value-list
-
specifies the value under the null hypothesis for testing the
estimable functions in the ESTIMATE statement. The rules for specifying the value-list are very similar to those for specifying the divisor list in the DIVISOR=
option. If no TESTVALUE= is specified, all tests are performed as 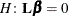 . Missing values in the value-list also are translated to zeros. If you specify fewer values than rows in the ESTIMATE statement, the last value in value-list is carried forward.
. Missing values in the value-list also are translated to zeros. If you specify fewer values than rows in the ESTIMATE statement, the last value in value-list is carried forward.
The TESTVALUE= option affects only p-values from individual, joint, and multiplicity-adjusted tests. It does not affect confidence intervals.
The TESTVALUE option is not available for the multinomial distribution, and the values are ignored when you perform a sampling-based
(Bayesian) analysis.
-
UPPER
UPPERTAILED
-
requests that the p-value for the t test be based only
on values that are greater than the test statistic. A two-tailed test is the default. An upper-tailed confidence limit is
also produced if you specify the CL
or ALPHA=
option.
Note that for ADJUST=
SCHEFFE the one-sided adjusted confidence intervals and one-sided adjusted p-values are the same as the corresponding two-sided statistics, because this adjustment is based on only the right tail of
the F distribution.
If you request a joint test with the JOINT
option, then a one-sided right-tailed order restriction is applied to all estimable functions, and the corresponding chi-bar-square
statistic of Silvapulle and Sen (2004) is computed in addition to the two-sided, standard, F or chi-square statistic. See the JOINT
option for how to control the computation of the simulation-based chi-bar-square statistic.
 matrix and are associated with the fixed and random effects. There are two basic methods of specifying the entries of the
matrix and are associated with the fixed and random effects. There are two basic methods of specifying the entries of the
 matrix. The traditional representation—also known as the positional syntax—relies on entering coefficients in the position
they assume in the
matrix. The traditional representation—also known as the positional syntax—relies on entering coefficients in the position
they assume in the  matrix. For example, in the following statements the elements of
matrix. For example, in the following statements the elements of  that are associated with the
that are associated with the  matrix from the level indicators is optional. Further details about the nonpositional contrast syntax and its use with constructed
effects can be found in the section Positional and Nonpositional Syntax for Coefficients in Linear Functions.
matrix from the level indicators is optional. Further details about the nonpositional contrast syntax and its use with constructed
effects can be found in the section Positional and Nonpositional Syntax for Coefficients in Linear Functions.
 to test the hypothesis
to test the hypothesis 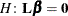 . The procedure supports nonpositional syntax for the coefficients of model effects in the ESTIMATE statement. For details
see the section Positional and Nonpositional Syntax for Coefficients in Linear Functions.
. The procedure supports nonpositional syntax for the coefficients of model effects in the ESTIMATE statement. For details
see the section Positional and Nonpositional Syntax for Coefficients in Linear Functions.
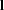 of
of  an approximate t test of the hypothesis
an approximate t test of the hypothesis 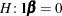 . You can also obtain multiplicity-adjusted p-values and confidence limits for multirow estimates with the ADJUST=
option.
. You can also obtain multiplicity-adjusted p-values and confidence limits for multirow estimates with the ADJUST=
option.

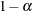

![\[ \frac{1}{1+\exp \{ -(\alpha _1 - \alpha _2)\} } \]](images/statug_introcom0095.png)
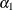
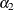
![\[ \pi _1 - \pi _2 = \frac{1}{1+\exp \{ -\beta _0 - \alpha _1\} } - \frac{1}{1+\exp \{ -\beta _0 - \alpha _2\} } \]](images/statug_introcom0098.png)