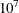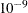The GENMOD Procedure
-
Overview

-
Getting Started

-
Syntax
 PROC GENMOD StatementASSESS StatementBAYES StatementBY StatementCLASS StatementCODE StatementCONTRAST StatementDEVIANCE StatementEFFECTPLOT StatementESTIMATE StatementEXACT StatementEXACTOPTIONS StatementFREQ StatementFWDLINK StatementINVLINK StatementLSMEANS StatementLSMESTIMATE StatementMODEL StatementOUTPUT StatementProgramming StatementsREPEATED StatementSLICE StatementSTORE StatementSTRATA StatementVARIANCE StatementWEIGHT StatementZEROMODEL Statement
PROC GENMOD StatementASSESS StatementBAYES StatementBY StatementCLASS StatementCODE StatementCONTRAST StatementDEVIANCE StatementEFFECTPLOT StatementESTIMATE StatementEXACT StatementEXACTOPTIONS StatementFREQ StatementFWDLINK StatementINVLINK StatementLSMEANS StatementLSMESTIMATE StatementMODEL StatementOUTPUT StatementProgramming StatementsREPEATED StatementSLICE StatementSTORE StatementSTRATA StatementVARIANCE StatementWEIGHT StatementZEROMODEL Statement -
Details
 Generalized Linear Models TheorySpecification of EffectsParameterization Used in PROC GENMODType 1 AnalysisType 3 AnalysisConfidence Intervals for ParametersF StatisticsLagrange Multiplier StatisticsPredicted Values of the MeanResidualsMultinomial ModelsZero-Inflated ModelsTweedie Distribution For Generalized Linear ModelsGeneralized Estimating EquationsAssessment of Models Based on Aggregates of ResidualsCase Deletion Diagnostic StatisticsBayesian AnalysisExact Logistic and Exact Poisson RegressionResponse Level OrderingMissing ValuesDisplayed Output for Classical AnalysisDisplayed Output for Bayesian AnalysisDisplayed Output for Exact AnalysisODS Table NamesODS Graphics
Generalized Linear Models TheorySpecification of EffectsParameterization Used in PROC GENMODType 1 AnalysisType 3 AnalysisConfidence Intervals for ParametersF StatisticsLagrange Multiplier StatisticsPredicted Values of the MeanResidualsMultinomial ModelsZero-Inflated ModelsTweedie Distribution For Generalized Linear ModelsGeneralized Estimating EquationsAssessment of Models Based on Aggregates of ResidualsCase Deletion Diagnostic StatisticsBayesian AnalysisExact Logistic and Exact Poisson RegressionResponse Level OrderingMissing ValuesDisplayed Output for Classical AnalysisDisplayed Output for Bayesian AnalysisDisplayed Output for Exact AnalysisODS Table NamesODS Graphics -
Examples
 Logistic RegressionNormal Regression, Log Link Gamma Distribution Applied to Life DataOrdinal Model for Multinomial DataGEE for Binary Data with Logit Link FunctionLog Odds Ratios and the ALR AlgorithmLog-Linear Model for Count DataModel Assessment of Multiple Regression Using Aggregates of ResidualsAssessment of a Marginal Model for Dependent DataBayesian Analysis of a Poisson Regression ModelExact Poisson RegressionTweedie Regression
Logistic RegressionNormal Regression, Log Link Gamma Distribution Applied to Life DataOrdinal Model for Multinomial DataGEE for Binary Data with Logit Link FunctionLog Odds Ratios and the ALR AlgorithmLog-Linear Model for Count DataModel Assessment of Multiple Regression Using Aggregates of ResidualsAssessment of a Marginal Model for Dependent DataBayesian Analysis of a Poisson Regression ModelExact Poisson RegressionTweedie Regression - References
MODEL Statement
-
MODEL response <(variable-options)> = <effects> </ options>;
-
MODEL events/trials = <effects> </ options>;
The MODEL statement specifies the response, or dependent variable, and the effects, or explanatory variables. If you omit the explanatory variables, the procedure fits an intercept-only model. An intercept term is included in the model by default. The intercept can be removed with the NOINT option.
You can specify the response in the form of a single variable or in the form of a ratio of two variables denoted events/trials. The first form is applicable to all responses. The second form is applicable only to summarized binomial response data. When each observation in the input data set contains the number of events (for example, successes) and the number of trials from a set of binomial trials, use the events/trials syntax.
In the events/trials model syntax, you specify two variables that contain the event and trial counts. These two variables are separated by a slash (/). The values of both events and (trials–events) must be nonnegative, and the value of the trials variable must be greater than 0 for an observation to be valid. The variable events or trials can take noninteger values.
When each observation in the input data set contains a single trial from a binomial or multinomial experiment, use the first form of the preceding MODEL statements. The response variable can be numeric or character. Variable options specific to the response variable can be specified in parentheses immediately after the response variable. Identifying the event level for binomial responses and ordering of response levels for multinomial responses is critical in these models. You can use the response variable options to do this.
Responses for the Poisson distribution must be all nonnegative, but they can be noninteger values.
The effects in the MODEL statement consist of an explanatory variable or combination of variables. Explanatory variables can be continuous or classification variables. Classification variables can be character or numeric. Explanatory variables representing nominal, or classification, data must be declared in a CLASS statement. Interactions between variables can also be included as effects. Columns of the design matrix are automatically generated for classification variables and interactions. The syntax for specification of effects is the same as for the GLM procedure. See the section Specification of Effects for more information. Also see Chapter 46: The GLM Procedure.
Response Variable Options
Table 44.7 summarizes the options available in the MODEL statement.
Table 44.7: MODEL Statement Options
|
Option |
Description |
|---|---|
|
Specifies the subpopulations |
|
|
Sets the confidence coefficient |
|
|
Sets the convergence criterion for profile likelihood confidence intervals |
|
|
Displays confidence limits for predicted values |
|
|
Uses effect coding for all classification variables |
|
|
Sets the convergence criterion |
|
|
Sets the relative Hessian convergence criterion |
|
|
Displays the parameter estimate correlation matrix |
|
|
Displays the parameter estimate covariance matrix |
|
|
Reverses the order of the response categories |
|
|
Displays case deletion diagnostic statistics |
|
|
Specifies the built-in probability distribution |
|
|
Specifies the event category for the binary response model |
|
|
Names a variable used for performing an exact Poisson regression |
|
|
Computes covariances and associated statistics by using the expected Fisher information matrix |
|
|
Displays the values of variable in the input data set in the OBSTATS table |
|
|
Sets initial values for parameter estimates |
|
|
Initializes the intercept term |
|
|
Displays the iteration history for all iterative processes |
|
|
Specifies the link function |
|
|
Computes the maximum likelihood estimate and confidence limits of k-based |
|
|
Computes two-sided confidence intervals for the partially likelihood function |
|
|
Sets the maximum allowable number of iterations for all iterative computation processes |
|
|
Requests that no intercept term |
|
|
Computes the maximum likelihood estimate and confidence limits of k based on k |
|
|
Holds the scale parameter fixed |
|
|
Displays an additional table of statistics |
|
|
Specifies a variable in the input data set to be used as an offset |
|
|
Specifies the sort order for the levels of the response variable |
|
|
Displays predicted values and associated statistics |
|
|
Specifies the reference category for the binary response model |
|
|
Displays residuals and standardized residuals |
|
|
Sets the value used for the scale |
|
|
Computes the Hessian matrix using the Fisher scoring method |
|
|
Sets the tolerance for testing singularity |
|
|
Performs a Type 1 analysis |
|
|
Computes statistics for Type 3 contrasts |
|
|
Requests Wald statistics for Type 3 contrasts |
|
|
Computes two-sided Wald confidence intervals |
|
|
Includes the regression variables in the OBSTATS table |
You can specify the following options in the MODEL statement after a slash (/).
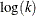
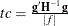
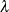
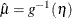
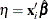
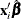
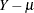
![\[ \frac{Y - \mu }{\sqrt {V(\mu ) / w}} \]](images/statug_genmod0148.png)
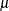
![$\hat{\beta } - \hat{\beta _{[i]}}$](images/statug_genmod0149.png)
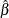
![$ \hat{\beta _{[i]}}$](images/statug_genmod0151.png)