The GENMOD Procedure
-
Overview

-
Getting Started

-
Syntax
 PROC GENMOD StatementASSESS StatementBAYES StatementBY StatementCLASS StatementCODE StatementCONTRAST StatementDEVIANCE StatementEFFECTPLOT StatementESTIMATE StatementEXACT StatementEXACTOPTIONS StatementFREQ StatementFWDLINK StatementINVLINK StatementLSMEANS StatementLSMESTIMATE StatementMODEL StatementOUTPUT StatementProgramming StatementsREPEATED StatementSLICE StatementSTORE StatementSTRATA StatementVARIANCE StatementWEIGHT StatementZEROMODEL Statement
PROC GENMOD StatementASSESS StatementBAYES StatementBY StatementCLASS StatementCODE StatementCONTRAST StatementDEVIANCE StatementEFFECTPLOT StatementESTIMATE StatementEXACT StatementEXACTOPTIONS StatementFREQ StatementFWDLINK StatementINVLINK StatementLSMEANS StatementLSMESTIMATE StatementMODEL StatementOUTPUT StatementProgramming StatementsREPEATED StatementSLICE StatementSTORE StatementSTRATA StatementVARIANCE StatementWEIGHT StatementZEROMODEL Statement -
Details
 Generalized Linear Models TheorySpecification of EffectsParameterization Used in PROC GENMODType 1 AnalysisType 3 AnalysisConfidence Intervals for ParametersF StatisticsLagrange Multiplier StatisticsPredicted Values of the MeanResidualsMultinomial ModelsZero-Inflated ModelsTweedie Distribution For Generalized Linear ModelsGeneralized Estimating EquationsAssessment of Models Based on Aggregates of ResidualsCase Deletion Diagnostic StatisticsBayesian AnalysisExact Logistic and Exact Poisson RegressionResponse Level OrderingMissing ValuesDisplayed Output for Classical AnalysisDisplayed Output for Bayesian AnalysisDisplayed Output for Exact AnalysisODS Table NamesODS Graphics
Generalized Linear Models TheorySpecification of EffectsParameterization Used in PROC GENMODType 1 AnalysisType 3 AnalysisConfidence Intervals for ParametersF StatisticsLagrange Multiplier StatisticsPredicted Values of the MeanResidualsMultinomial ModelsZero-Inflated ModelsTweedie Distribution For Generalized Linear ModelsGeneralized Estimating EquationsAssessment of Models Based on Aggregates of ResidualsCase Deletion Diagnostic StatisticsBayesian AnalysisExact Logistic and Exact Poisson RegressionResponse Level OrderingMissing ValuesDisplayed Output for Classical AnalysisDisplayed Output for Bayesian AnalysisDisplayed Output for Exact AnalysisODS Table NamesODS Graphics -
Examples
 Logistic RegressionNormal Regression, Log Link Gamma Distribution Applied to Life DataOrdinal Model for Multinomial DataGEE for Binary Data with Logit Link FunctionLog Odds Ratios and the ALR AlgorithmLog-Linear Model for Count DataModel Assessment of Multiple Regression Using Aggregates of ResidualsAssessment of a Marginal Model for Dependent DataBayesian Analysis of a Poisson Regression ModelExact Poisson RegressionTweedie Regression
Logistic RegressionNormal Regression, Log Link Gamma Distribution Applied to Life DataOrdinal Model for Multinomial DataGEE for Binary Data with Logit Link FunctionLog Odds Ratios and the ALR AlgorithmLog-Linear Model for Count DataModel Assessment of Multiple Regression Using Aggregates of ResidualsAssessment of a Marginal Model for Dependent DataBayesian Analysis of a Poisson Regression ModelExact Poisson RegressionTweedie Regression - References
Example 44.5 GEE for Binary Data with Logit Link Function
Output 44.5.1 displays a partial listing of a SAS data set of clinical trial data comparing two treatments for a respiratory disorder. See "Gee Model for Binary Data" in the SAS/STAT Sample Program Library for the complete data set. These data are from Stokes, Davis, and Koch (2000).
Patients in each of two centers are randomly assigned to groups receiving the active treatment or a placebo. During treatment,
respiratory status, represented by the variable outcome (coded here as 0=poor, 1=good), is determined for each of four visits. The variables center, treatment, sex, and baseline (baseline respiratory status) are classification variables with two levels. The variable age (age at time of entry into the study) is a continuous variable.
Explanatory variables in the model are Intercept (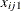 ),
), treatment (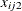 ),
), center (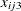 ),
), sex (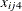 ),
), age (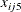 ), and
), and baseline (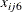 ), so that
), so that ![$x^\prime =[x_{ij1},x_{ij2},\ldots ,x_{ij6}]$](images/statug_genmod0678.png) is the vector of explanatory variables. Indicator variables for the classification explanatory variables can be automatically
generated by listing them in the CLASS statement in PROC GENMOD. To be consistent with the analysis in Stokes, Davis, and
Koch (2000), the four classification explanatory variables are coded as follows via options in the CLASS statement:
is the vector of explanatory variables. Indicator variables for the classification explanatory variables can be automatically
generated by listing them in the CLASS statement in PROC GENMOD. To be consistent with the analysis in Stokes, Davis, and
Koch (2000), the four classification explanatory variables are coded as follows via options in the CLASS statement:
![\[ \begin{array}{llllll} x_{ij2}& =& \left\{ \begin{array}{l} \mbox{0 placebo} \\ \mbox{1 active} \end{array}\right.& x_{ij3}& =& \left\{ \begin{array}{l} \mbox{0 center 1} \\ \mbox{1 center 2} \end{array}\right. \\ \end{array} \]](images/statug_genmod0679.png)
![\[ \begin{array}{llllll} x_{ij4}& =& \left\{ \begin{array}{l} \mbox{0 male} \\ \mbox{1 female} \end{array}\right. & x_{ij6}& =& \left\{ \begin{array}{l} \mbox{0 0} \\ \mbox{1 1} \end{array}\right. \\ \end{array} \]](images/statug_genmod0680.png)
Suppose 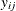 represents the respiratory status of patient i at the jth visit,
represents the respiratory status of patient i at the jth visit, 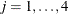 , and
, and 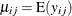 represents the mean of the respiratory status. Since the response data are binary, you can use the variance function for
the binomial distribution
represents the mean of the respiratory status. Since the response data are binary, you can use the variance function for
the binomial distribution 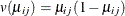 and the logit link function
and the logit link function 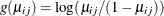 . The model for the mean is
. The model for the mean is 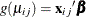 , where
, where 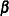 is a vector of regression parameters to be estimated.
is a vector of regression parameters to be estimated.
Output 44.5.1: Respiratory Disorder Data
| Obs | center | id | treatment | sex | age | baseline | visit1 | visit2 | visit3 | visit4 | visit | outcome |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 1 | P | M | 46 | 0 | 0 | 0 | 0 | 0 | 1 | 0 |
| 2 | 1 | 1 | P | M | 46 | 0 | 0 | 0 | 0 | 0 | 2 | 0 |
| 3 | 1 | 1 | P | M | 46 | 0 | 0 | 0 | 0 | 0 | 3 | 0 |
| 4 | 1 | 1 | P | M | 46 | 0 | 0 | 0 | 0 | 0 | 4 | 0 |
| 5 | 1 | 2 | P | M | 28 | 0 | 0 | 0 | 0 | 0 | 1 | 0 |
| 6 | 1 | 2 | P | M | 28 | 0 | 0 | 0 | 0 | 0 | 2 | 0 |
| 7 | 1 | 2 | P | M | 28 | 0 | 0 | 0 | 0 | 0 | 3 | 0 |
| 8 | 1 | 2 | P | M | 28 | 0 | 0 | 0 | 0 | 0 | 4 | 0 |
| . | ||||||||||||
| . | ||||||||||||
| . | ||||||||||||
| 214 | 2 | 1 | P | F | 39 | 0 | 0 | 0 | 0 | 0 | 1 | 0 |
| 215 | 2 | 1 | P | F | 39 | 0 | 0 | 0 | 0 | 0 | 2 | 0 |
| 216 | 2 | 1 | P | F | 39 | 0 | 0 | 0 | 0 | 0 | 3 | 0 |
| 217 | 2 | 1 | P | F | 39 | 0 | 0 | 0 | 0 | 0 | 4 | 0 |
| 218 | 2 | 2 | A | M | 25 | 0 | 0 | 1 | 1 | 1 | 1 | 0 |
| 219 | 2 | 2 | A | M | 25 | 0 | 0 | 1 | 1 | 1 | 2 | 1 |
| 220 | 2 | 2 | A | M | 25 | 0 | 0 | 1 | 1 | 1 | 3 | 1 |
| 221 | 2 | 2 | A | M | 25 | 0 | 0 | 1 | 1 | 1 | 4 | 1 |
| . | ||||||||||||
| . | ||||||||||||
| . | ||||||||||||
| . |
The GEE solution is requested with the REPEATED statement in the GENMOD procedure. The option SUBJECT=ID(CENTER) specifies
that the observations in any single cluster are uniquely identified by both center and id. An equivalent specification is SUBJECT=ID*CENTER. Since the same id values are used in each center, one of these specifications is needed. If id values were unique across all centers, SUBJECT=ID would be specified.
The option TYPE=UNSTR specifies the unstructured working correlation structure. The MODEL statement specifies the regression model for the mean with the binomial distribution variance function. The following SAS statements perform the GEE model fit:
proc genmod data=resp descend;
class id treatment(ref="P") center(ref="1") sex(ref="M")
baseline(ref="0") / param=ref;
model outcome=treatment center sex age baseline / dist=bin;
repeated subject=id(center) / corr=unstr corrw;
run;
These statements first fit the generalized linear (GLM) model specified in the MODEL statement. The parameter estimates from
the generalized linear model fit are not shown in the output, but they are used as initial values for the GEE solution. The
DESCEND option in the PROC GENMOD statement specifies that the probability that outcome = 1 be modeled. If the DESCEND option had not been specified, the probability that outcome = 0 would be modeled by default.
Information about the GEE model is displayed in Output 44.5.2. The results of GEE model fitting are displayed in Output 44.5.3. Model goodness-of-fit criteria are displayed in Output 44.5.4. If you specify no other options, the standard errors, confidence intervals, Z scores, and p-values are based on empirical standard error estimates. You can specify the MODELSE option in the REPEATED statement to create a table based on model-based standard error estimates.
Output 44.5.2: Model Fitting Information
Output 44.5.3: Results of Model Fitting
| Analysis Of GEE Parameter Estimates | |||||||
|---|---|---|---|---|---|---|---|
| Empirical Standard Error Estimates | |||||||
| Parameter | Estimate | Standard Error |
95% Confidence Limits | Z | Pr > |Z| | ||
| Intercept | -0.8882 | 0.4568 | -1.7835 | 0.0071 | -1.94 | 0.0519 | |
| treatment | A | 1.2442 | 0.3455 | 0.5669 | 1.9214 | 3.60 | 0.0003 |
| center | 2 | 0.6558 | 0.3512 | -0.0326 | 1.3442 | 1.87 | 0.0619 |
| sex | F | 0.1128 | 0.4408 | -0.7512 | 0.9768 | 0.26 | 0.7981 |
| age | -0.0175 | 0.0129 | -0.0427 | 0.0077 | -1.36 | 0.1728 | |
| baseline | 1 | 1.8981 | 0.3441 | 1.2237 | 2.5725 | 5.52 | <.0001 |
The nonsignificance of age and sex make them candidates for omission from the model.