The GENMOD Procedure

Residuals

The GENMOD procedure computes three kinds of residuals. Residuals are available for all generalized linear models except multinomial models for ordinal response data, for which residuals are not available. Raw residuals and Pearson residuals are available for models fit with generalized estimating equations (GEEs).

The raw residual is defined as

\[ r_ i = y_ i - \mu _ i \]

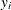where $y_ i$ is the ith response and 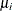$\mu _ i$ is the corresponding predicted mean. You can request raw residuals in an output data set with the keyword RESRAW in the OUTPUT statement.

The Pearson residual is the square root of the ith contribution to the Pearson’s chi-square:

\[ r_{Pi} = (y_ i - \mu _ i) \sqrt { \frac{w_ i}{V(\mu _ i)} } \]

You can request Pearson residuals in an output data set with the keyword RESCHI in the OUTPUT statement.

Finally, the deviance residual is defined as the square root of the contribution of the ith observation to the deviance, with the sign of the raw residual:

\[ r_{Di} = \sqrt {d_ i}(\mr{sign}(y_ i - \mu _ i)) \]

You can request deviance residuals in an output data set with the keyword RESDEV in the OUTPUT statement.

The adjusted Pearson, deviance, and likelihood residuals are defined by Agresti (2002); Williams (1987); Davison and Snell (1991). These residuals are useful for outlier detection and for assessing the influence of single observations on the fitted model.

For the generalized linear model, the variance of the ith individual observation is given by

\[ v_ i = \frac{\phi V(\mu _ i)}{w_ i} \]

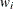where $\phi $ is the dispersion parameter, $w_ i$ is a user-specified prior weight (if not specified, 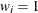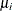$w_ i=1$), $\mu _ i$ is the mean, and 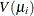$V(\mu _ i)$ is the variance function. Let

\[ w_{ei} = v_ i^{-1}(g^{\prime }(\mu _ i))^{-2} \]

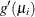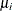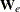for the ith observation, where $g^{\prime }(\mu _ i)$ is the derivative of the link function, evaluated at $\mu _ i$. Let $\mb{W}_ e$ be the diagonal matrix with 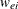$w_{ei}$ denoting the ith diagonal element. The weight matrix 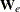$\mb{W}_ e$ is used in computing the expected information matrix.

Define 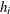$h_ i$ as the ith diagonal element of the matrix

\[ \mb{W}_ e^\frac {1}{2} \mb{X} (\mb{X}^{\prime } \mb{W}_ e \mb{X})^{-1} \mb{X}^{\prime } \mb{W}_ e^\frac {1}{2} \]

The Pearson residuals, standardized to have unit asymptotic variance, are given by

\[ r_{Pi} = \frac{y_ i - \mu _ i}{\sqrt {v_ i(1 - h_ i)}} \]

You can request standardized Pearson residuals in an output data set with the keyword STDRESCHI in the OUTPUT statement. The deviance residuals, standardized to have unit asymptotic variance, are given by

\[ r_{Di} = \frac{\mr{sign}(y_ i - \mu _ i) \sqrt {d_ i}}{\sqrt {\phi (1 - h_ i)}} \]

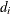where $d_ i$ is the contribution to the total deviance from observation i, and 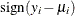$\mr{sign}(y_ i - \mu _ i)$ is 1 if 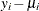$y_ i - \mu _ i$ is positive and –1 if 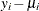$y_ i - \mu _ i$ is negative. You can request standardized deviance residuals in an output data set with the keyword STDRESDEV in the OUTPUT statement. The likelihood residuals are defined by

\[ r_{Gi} = \mr{sign}(y_ i - \mu _ i) \sqrt {(1 - h_ i)r_{Di}^2 + h_ i r_{Pi}^2} \]

You can request likelihood residuals in an output data set with the keyword RESLIK in the OUTPUT statement.