The GENMOD Procedure
-
Overview

-
Getting Started

-
Syntax
 PROC GENMOD StatementASSESS StatementBAYES StatementBY StatementCLASS StatementCODE StatementCONTRAST StatementDEVIANCE StatementEFFECTPLOT StatementESTIMATE StatementEXACT StatementEXACTOPTIONS StatementFREQ StatementFWDLINK StatementINVLINK StatementLSMEANS StatementLSMESTIMATE StatementMODEL StatementOUTPUT StatementProgramming StatementsREPEATED StatementSLICE StatementSTORE StatementSTRATA StatementVARIANCE StatementWEIGHT StatementZEROMODEL Statement
PROC GENMOD StatementASSESS StatementBAYES StatementBY StatementCLASS StatementCODE StatementCONTRAST StatementDEVIANCE StatementEFFECTPLOT StatementESTIMATE StatementEXACT StatementEXACTOPTIONS StatementFREQ StatementFWDLINK StatementINVLINK StatementLSMEANS StatementLSMESTIMATE StatementMODEL StatementOUTPUT StatementProgramming StatementsREPEATED StatementSLICE StatementSTORE StatementSTRATA StatementVARIANCE StatementWEIGHT StatementZEROMODEL Statement -
Details
 Generalized Linear Models TheorySpecification of EffectsParameterization Used in PROC GENMODType 1 AnalysisType 3 AnalysisConfidence Intervals for ParametersF StatisticsLagrange Multiplier StatisticsPredicted Values of the MeanResidualsMultinomial ModelsZero-Inflated ModelsTweedie Distribution For Generalized Linear ModelsGeneralized Estimating EquationsAssessment of Models Based on Aggregates of ResidualsCase Deletion Diagnostic StatisticsBayesian AnalysisExact Logistic and Exact Poisson RegressionResponse Level OrderingMissing ValuesDisplayed Output for Classical AnalysisDisplayed Output for Bayesian AnalysisDisplayed Output for Exact AnalysisODS Table NamesODS Graphics
Generalized Linear Models TheorySpecification of EffectsParameterization Used in PROC GENMODType 1 AnalysisType 3 AnalysisConfidence Intervals for ParametersF StatisticsLagrange Multiplier StatisticsPredicted Values of the MeanResidualsMultinomial ModelsZero-Inflated ModelsTweedie Distribution For Generalized Linear ModelsGeneralized Estimating EquationsAssessment of Models Based on Aggregates of ResidualsCase Deletion Diagnostic StatisticsBayesian AnalysisExact Logistic and Exact Poisson RegressionResponse Level OrderingMissing ValuesDisplayed Output for Classical AnalysisDisplayed Output for Bayesian AnalysisDisplayed Output for Exact AnalysisODS Table NamesODS Graphics -
Examples
 Logistic RegressionNormal Regression, Log Link Gamma Distribution Applied to Life DataOrdinal Model for Multinomial DataGEE for Binary Data with Logit Link FunctionLog Odds Ratios and the ALR AlgorithmLog-Linear Model for Count DataModel Assessment of Multiple Regression Using Aggregates of ResidualsAssessment of a Marginal Model for Dependent DataBayesian Analysis of a Poisson Regression ModelExact Poisson RegressionTweedie Regression
Logistic RegressionNormal Regression, Log Link Gamma Distribution Applied to Life DataOrdinal Model for Multinomial DataGEE for Binary Data with Logit Link FunctionLog Odds Ratios and the ALR AlgorithmLog-Linear Model for Count DataModel Assessment of Multiple Regression Using Aggregates of ResidualsAssessment of a Marginal Model for Dependent DataBayesian Analysis of a Poisson Regression ModelExact Poisson RegressionTweedie Regression - References
F Statistics
Suppose that  is the deviance resulting from fitting a generalized linear model and that
is the deviance resulting from fitting a generalized linear model and that  is the deviance from fitting a submodel. Then, under appropriate regularity conditions, the asymptotic distribution of
is the deviance from fitting a submodel. Then, under appropriate regularity conditions, the asymptotic distribution of  is chi-square with r degrees of freedom, where r is the difference in the number of parameters between the two models and
is chi-square with r degrees of freedom, where r is the difference in the number of parameters between the two models and  is the dispersion parameter. If
is the dispersion parameter. If  is unknown, and
is unknown, and 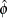 is an estimate of
is an estimate of  based on the deviance or Pearson’s chi-square divided by degrees of freedom, then, under regularity conditions,
based on the deviance or Pearson’s chi-square divided by degrees of freedom, then, under regularity conditions,  has an asymptotic chi-square distribution with
has an asymptotic chi-square distribution with 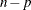 degrees of freedom. Here, n is the number of observations and p is the number of parameters in the model that is used to estimate
degrees of freedom. Here, n is the number of observations and p is the number of parameters in the model that is used to estimate  . Thus, the asymptotic distribution of
. Thus, the asymptotic distribution of
![\[ F = \frac{D_1-D_0}{r \hat{\phi }} \]](images/statug_genmod0284.png)
is the F distribution
with r and 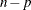 degrees of freedom, assuming that
degrees of freedom, assuming that  and
and  are approximately independent.
are approximately independent.
This F statistic is computed for the Type 1 analysis, Type 3 analysis, and hypothesis tests specified in CONTRAST statements when the dispersion parameter is estimated by either the deviance or Pearson’s chi-square divided by degrees of freedom, as specified by the DSCALE or PSCALE option in the MODEL statement. In the case of a Type 1 analysis, model 0 is the higher-order model obtained by including one additional effect in model 1. For a Type 3 analysis and hypothesis tests, model 0 is the full specified model and model 1 is the submodel obtained from constraining the Type III contrast or the user-specified contrast to be 0.