The GENMOD Procedure
-
Overview

-
Getting Started

-
Syntax
 PROC GENMOD StatementASSESS StatementBAYES StatementBY StatementCLASS StatementCODE StatementCONTRAST StatementDEVIANCE StatementEFFECTPLOT StatementESTIMATE StatementEXACT StatementEXACTOPTIONS StatementFREQ StatementFWDLINK StatementINVLINK StatementLSMEANS StatementLSMESTIMATE StatementMODEL StatementOUTPUT StatementProgramming StatementsREPEATED StatementSLICE StatementSTORE StatementSTRATA StatementVARIANCE StatementWEIGHT StatementZEROMODEL Statement
PROC GENMOD StatementASSESS StatementBAYES StatementBY StatementCLASS StatementCODE StatementCONTRAST StatementDEVIANCE StatementEFFECTPLOT StatementESTIMATE StatementEXACT StatementEXACTOPTIONS StatementFREQ StatementFWDLINK StatementINVLINK StatementLSMEANS StatementLSMESTIMATE StatementMODEL StatementOUTPUT StatementProgramming StatementsREPEATED StatementSLICE StatementSTORE StatementSTRATA StatementVARIANCE StatementWEIGHT StatementZEROMODEL Statement -
Details
 Generalized Linear Models TheorySpecification of EffectsParameterization Used in PROC GENMODType 1 AnalysisType 3 AnalysisConfidence Intervals for ParametersF StatisticsLagrange Multiplier StatisticsPredicted Values of the MeanResidualsMultinomial ModelsZero-Inflated ModelsTweedie Distribution For Generalized Linear ModelsGeneralized Estimating EquationsAssessment of Models Based on Aggregates of ResidualsCase Deletion Diagnostic StatisticsBayesian AnalysisExact Logistic and Exact Poisson RegressionResponse Level OrderingMissing ValuesDisplayed Output for Classical AnalysisDisplayed Output for Bayesian AnalysisDisplayed Output for Exact AnalysisODS Table NamesODS Graphics
Generalized Linear Models TheorySpecification of EffectsParameterization Used in PROC GENMODType 1 AnalysisType 3 AnalysisConfidence Intervals for ParametersF StatisticsLagrange Multiplier StatisticsPredicted Values of the MeanResidualsMultinomial ModelsZero-Inflated ModelsTweedie Distribution For Generalized Linear ModelsGeneralized Estimating EquationsAssessment of Models Based on Aggregates of ResidualsCase Deletion Diagnostic StatisticsBayesian AnalysisExact Logistic and Exact Poisson RegressionResponse Level OrderingMissing ValuesDisplayed Output for Classical AnalysisDisplayed Output for Bayesian AnalysisDisplayed Output for Exact AnalysisODS Table NamesODS Graphics -
Examples
 Logistic RegressionNormal Regression, Log Link Gamma Distribution Applied to Life DataOrdinal Model for Multinomial DataGEE for Binary Data with Logit Link FunctionLog Odds Ratios and the ALR AlgorithmLog-Linear Model for Count DataModel Assessment of Multiple Regression Using Aggregates of ResidualsAssessment of a Marginal Model for Dependent DataBayesian Analysis of a Poisson Regression ModelExact Poisson RegressionTweedie Regression
Logistic RegressionNormal Regression, Log Link Gamma Distribution Applied to Life DataOrdinal Model for Multinomial DataGEE for Binary Data with Logit Link FunctionLog Odds Ratios and the ALR AlgorithmLog-Linear Model for Count DataModel Assessment of Multiple Regression Using Aggregates of ResidualsAssessment of a Marginal Model for Dependent DataBayesian Analysis of a Poisson Regression ModelExact Poisson RegressionTweedie Regression - References
ESTIMATE Statement
-
ESTIMATE 'label' contrast-specification </ options> ;
The ESTIMATE statement is similar to a CONTRAST statement, except only one-row 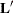 matrices are permitted.
matrices are permitted.
The elements of the ESTIMATE statement are as follows:
- label
-
identifies the contrast on the output. A label is required for every contrast specified. Labels can be up to 20 characters and must be enclosed in single quotes.
- contrast-specification
-
identifies the effects and their coefficients from which the
 matrix is formed. The contrast-specification can be specified in two different ways. The first method applies to all models except the zero-inflated (ZI) distributions
(zero-inflated Poisson and zero-inflated negative binomial), and the syntax is:
matrix is formed. The contrast-specification can be specified in two different ways. The first method applies to all models except the zero-inflated (ZI) distributions
(zero-inflated Poisson and zero-inflated negative binomial), and the syntax is:
effect values <…effect values>
The second method of specifying a contrast applies only to ZI models, and the syntax is:
effect values <…effect values> @ZERO effect values <…effect values>
where
- effect
-
identifies an effect that appears in the MODEL statement. The value INTERCEPT or intercept can be used as an effect when an intercept is included in the model. You do not need to include all effects that are included in the MODEL statement.
- values
-
are constants that are elements of the
 vector associated with the effect.
vector associated with the effect.
- options
-
specifies options for the ESTIMATE statement.
For ZI models, sets of effects values before the @ZERO separator correspond to the regression part of the model with regression parameters 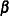 , and effects values after the @ZERO separator correspond to the zero-inflation part of the model with regression parameters
, and effects values after the @ZERO separator correspond to the zero-inflation part of the model with regression parameters 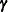 . In the case of ZI models, a one-row
. In the case of ZI models, a one-row 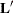 matrix is created for the regression part of the model, another one-row
matrix is created for the regression part of the model, another one-row 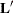 matrix is created for the zero-inflation part of the model, and separate estimates for the two
matrix is created for the zero-inflation part of the model, and separate estimates for the two  matrices are computed and displayed.
matrices are computed and displayed.
If you use the default less-than-full-rank GLM CLASS variable parameterization, each row is checked for estimability. If PROC GENMOD finds a contrast to be nonestimable, it displays missing values in corresponding rows in the results. See Searle (1971) for a discussion of estimable functions.
The actual estimate, 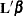 (and
(and 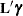 for ZI models), its approximate standard error, and confidence limits are displayed. Additionally, the corresponding estimate
on the mean scale (defined as the inverse link function applied to
for ZI models), its approximate standard error, and confidence limits are displayed. Additionally, the corresponding estimate
on the mean scale (defined as the inverse link function applied to 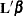 ), and confidence limits are displayed. Wald chi-square tests that
), and confidence limits are displayed. Wald chi-square tests that 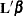 = 0 and
= 0 and 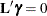 are also displayed.
are also displayed.
The approximate standard error of the estimate is computed as the square root of 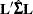 , where
, where 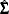 is the estimated covariance matrix of the parameter estimates. If you specify a GEE model in the REPEATED statement,
is the estimated covariance matrix of the parameter estimates. If you specify a GEE model in the REPEATED statement, 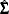 is the empirical covariance matrix estimate.
is the empirical covariance matrix estimate.
If you specify the EXP option, then 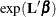 , its standard error, and its confidence limits are also displayed.
, its standard error, and its confidence limits are also displayed.
The construction of the  vector and the checking for estimability for an ESTIMATE statement follow the same rules as listed under the CONTRAST statement.
vector and the checking for estimability for an ESTIMATE statement follow the same rules as listed under the CONTRAST statement.
You can specify the following options in the ESTIMATE statement after a slash (/).