The GENMOD Procedure
-
Overview

-
Getting Started

-
Syntax
 PROC GENMOD StatementASSESS StatementBAYES StatementBY StatementCLASS StatementCODE StatementCONTRAST StatementDEVIANCE StatementEFFECTPLOT StatementESTIMATE StatementEXACT StatementEXACTOPTIONS StatementFREQ StatementFWDLINK StatementINVLINK StatementLSMEANS StatementLSMESTIMATE StatementMODEL StatementOUTPUT StatementProgramming StatementsREPEATED StatementSLICE StatementSTORE StatementSTRATA StatementVARIANCE StatementWEIGHT StatementZEROMODEL Statement
PROC GENMOD StatementASSESS StatementBAYES StatementBY StatementCLASS StatementCODE StatementCONTRAST StatementDEVIANCE StatementEFFECTPLOT StatementESTIMATE StatementEXACT StatementEXACTOPTIONS StatementFREQ StatementFWDLINK StatementINVLINK StatementLSMEANS StatementLSMESTIMATE StatementMODEL StatementOUTPUT StatementProgramming StatementsREPEATED StatementSLICE StatementSTORE StatementSTRATA StatementVARIANCE StatementWEIGHT StatementZEROMODEL Statement -
Details
 Generalized Linear Models TheorySpecification of EffectsParameterization Used in PROC GENMODType 1 AnalysisType 3 AnalysisConfidence Intervals for ParametersF StatisticsLagrange Multiplier StatisticsPredicted Values of the MeanResidualsMultinomial ModelsZero-Inflated ModelsTweedie Distribution For Generalized Linear ModelsGeneralized Estimating EquationsAssessment of Models Based on Aggregates of ResidualsCase Deletion Diagnostic StatisticsBayesian AnalysisExact Logistic and Exact Poisson RegressionResponse Level OrderingMissing ValuesDisplayed Output for Classical AnalysisDisplayed Output for Bayesian AnalysisDisplayed Output for Exact AnalysisODS Table NamesODS Graphics
Generalized Linear Models TheorySpecification of EffectsParameterization Used in PROC GENMODType 1 AnalysisType 3 AnalysisConfidence Intervals for ParametersF StatisticsLagrange Multiplier StatisticsPredicted Values of the MeanResidualsMultinomial ModelsZero-Inflated ModelsTweedie Distribution For Generalized Linear ModelsGeneralized Estimating EquationsAssessment of Models Based on Aggregates of ResidualsCase Deletion Diagnostic StatisticsBayesian AnalysisExact Logistic and Exact Poisson RegressionResponse Level OrderingMissing ValuesDisplayed Output for Classical AnalysisDisplayed Output for Bayesian AnalysisDisplayed Output for Exact AnalysisODS Table NamesODS Graphics -
Examples
 Logistic RegressionNormal Regression, Log Link Gamma Distribution Applied to Life DataOrdinal Model for Multinomial DataGEE for Binary Data with Logit Link FunctionLog Odds Ratios and the ALR AlgorithmLog-Linear Model for Count DataModel Assessment of Multiple Regression Using Aggregates of ResidualsAssessment of a Marginal Model for Dependent DataBayesian Analysis of a Poisson Regression ModelExact Poisson RegressionTweedie Regression
Logistic RegressionNormal Regression, Log Link Gamma Distribution Applied to Life DataOrdinal Model for Multinomial DataGEE for Binary Data with Logit Link FunctionLog Odds Ratios and the ALR AlgorithmLog-Linear Model for Count DataModel Assessment of Multiple Regression Using Aggregates of ResidualsAssessment of a Marginal Model for Dependent DataBayesian Analysis of a Poisson Regression ModelExact Poisson RegressionTweedie Regression - References
Example 44.10 Bayesian Analysis of a Poisson Regression Model
This example illustrates a Bayesian analysis of a log-linear Poisson regression model. Consider the following data on patients from clinical trials. The data set is a subset of the data described in Ibrahim, Chen, and Lipsitz (1999).
data Liver; input X1-X6 Y; datalines; 19.1358 50.0110 51.000 0 0 1 3 23.5970 18.4959 3.429 0 0 1 9 20.0474 56.7699 3.429 1 1 0 6 28.0277 59.7836 4.000 0 0 1 6 28.6851 74.1589 5.714 1 0 1 1 18.8092 31.0630 2.286 0 1 1 61 28.7201 52.9178 37.286 1 0 1 6 21.3669 61.6603 54.143 0 1 1 6 23.7332 42.2904 0.571 1 0 1 21 20.4783 22.1260 19.000 1 0 1 6 ... more lines ... 17.0993 48.8384 3.000 0 0 0 9 19.1327 65.3425 2.571 1 0 0 1 17.3010 51.4493 4.429 1 0 0 6 ;
The primary interest is in prediction of the number of cancerous liver nodes when a patient enters the trials, by using six other baseline characteristics. The number of nodes is modeled by a Poisson regression model with the six baseline characteristics as covariates. The response and regression variables are as follows:
|
|
Number of Cancerous Liver Nodes |
|
|
Body Mass Index |
|
|
Age, in Years |
|
|
Time Since Diagnosis of Disease, in Weeks |
|
|
Two Biochemical Markers (each classified as normal=1 or abnormal=0) |
|
|
Anti Hepatitis B Antigen |
|
|
Associated Jaundice (yes=1, no=0) |
Two analyses are performed using PROC GENMOD. The first analysis uses noninformative normal prior distributions, and the second analysis uses an informative normal prior for one of the regression parameters.
In the following BAYES statement, COEFFPRIOR=NORMAL specifies a noninformative independent normal prior distribution with
zero mean and variance  for each parameter.
for each parameter.
The initial analysis is performed using PROC GENMOD to obtain Bayesian estimates of the regression coefficients by using the following SAS statements:
proc genmod data=Liver; model Y = X1-X6 / dist=Poisson link=log; bayes seed=1 coeffprior=normal; run;
Maximum likelihood estimates of the model parameters are computed by default. These are shown in the "Analysis of Maximum Likelihood Parameter Estimates" table in Output 44.10.1.
Output 44.10.1: Maximum Likelihood Parameter Estimates
| Analysis Of Maximum Likelihood Parameter Estimates | |||||
|---|---|---|---|---|---|
| Parameter | DF | Estimate | Standard Error |
Wald 95% Confidence Limits | |
| Intercept | 1 | 2.4508 | 0.2284 | 2.0032 | 2.8984 |
| X1 | 1 | -0.0044 | 0.0080 | -0.0201 | 0.0114 |
| X2 | 1 | -0.0135 | 0.0024 | -0.0181 | -0.0088 |
| X3 | 1 | -0.0029 | 0.0022 | -0.0072 | 0.0014 |
| X4 | 1 | -0.2715 | 0.0795 | -0.4272 | -0.1157 |
| X5 | 1 | 0.3215 | 0.0832 | 0.1585 | 0.4845 |
| X6 | 1 | 0.2077 | 0.0827 | 0.0456 | 0.3698 |
| Scale | 0 | 1.0000 | 0.0000 | 1.0000 | 1.0000 |
| Note: | The scale parameter was held fixed. |
Noninformative independent normal prior distributions with zero means and variances of  were used in the initial analysis. These are shown in Output 44.10.2.
were used in the initial analysis. These are shown in Output 44.10.2.
Output 44.10.2: Regression Coefficient Priors
Initial values for the Markov chain are listed in the "Initial Values and Seeds" table in Output 44.10.3. The random number seed is also listed so that you can reproduce the analysis. Since no seed was specified, the seed shown was derived from the time of day.
Output 44.10.3: MCMC Initial Values and Seeds
Summary statistics for the posterior sample are displayed in the "Fit Statistics," "Descriptive Statistics for the Posterior Sample," "Interval Statistics for the Posterior Sample," and "Posterior Correlation Matrix" tables in Output 44.10.4, Output 44.10.5, Output 44.10.6, and Output 44.10.7, respectively. Since noninformative prior distributions for the regression coefficients were used, the mean and standard deviations of the posterior distributions for the model parameters are close to the maximum likelihood estimates and standard errors.
Output 44.10.4: Fit Statistics
Output 44.10.5: Descriptive Statistics
| Posterior Summaries | ||||||
|---|---|---|---|---|---|---|
| Parameter | N | Mean | Standard Deviation |
Percentiles | ||
| 25% | 50% | 75% | ||||
| Intercept | 10000 | 2.4483 | 0.2320 | 2.2903 | 2.4493 | 2.6093 |
| X1 | 10000 | -0.00475 | 0.00809 | -0.0101 | -0.00466 | 0.000851 |
| X2 | 10000 | -0.0134 | 0.00237 | -0.0150 | -0.0134 | -0.0118 |
| X3 | 10000 | -0.00303 | 0.00220 | -0.00445 | -0.00298 | -0.00150 |
| X4 | 10000 | -0.2703 | 0.0799 | -0.3241 | -0.2725 | -0.2190 |
| X5 | 10000 | 0.3202 | 0.0828 | 0.2642 | 0.3209 | 0.3775 |
| X6 | 10000 | 0.2106 | 0.0838 | 0.1533 | 0.2111 | 0.2663 |
Output 44.10.6: Interval Statistics
| Posterior Intervals | |||||
|---|---|---|---|---|---|
| Parameter | Alpha | Equal-Tail Interval | HPD Interval | ||
| Intercept | 0.050 | 1.9903 | 2.9059 | 2.0289 | 2.9321 |
| X1 | 0.050 | -0.0209 | 0.0108 | -0.0211 | 0.0106 |
| X2 | 0.050 | -0.0181 | -0.00870 | -0.0184 | -0.00908 |
| X3 | 0.050 | -0.00761 | 0.00105 | -0.00745 | 0.00113 |
| X4 | 0.050 | -0.4257 | -0.1063 | -0.4314 | -0.1152 |
| X5 | 0.050 | 0.1563 | 0.4804 | 0.1574 | 0.4811 |
| X6 | 0.050 | 0.0450 | 0.3777 | 0.0468 | 0.3788 |
Output 44.10.7: Posterior Sample Correlation Matrix
| Posterior Correlation Matrix | |||||||
|---|---|---|---|---|---|---|---|
| Parameter | Intercept | X1 | X2 | X3 | X4 | X5 | X6 |
| Intercept | 1.000 | -0.708 | -0.432 | -0.046 | -0.261 | -0.185 | -0.422 |
| X1 | -0.708 | 1.000 | -0.202 | -0.047 | -0.035 | 0.078 | 0.129 |
| X2 | -0.432 | -0.202 | 1.000 | 0.035 | 0.076 | 0.054 | 0.117 |
| X3 | -0.046 | -0.047 | 0.035 | 1.000 | 0.027 | -0.042 | -0.077 |
| X4 | -0.261 | -0.035 | 0.076 | 0.027 | 1.000 | -0.024 | 0.127 |
| X5 | -0.185 | 0.078 | 0.054 | -0.042 | -0.024 | 1.000 | -0.037 |
| X6 | -0.422 | 0.129 | 0.117 | -0.077 | 0.127 | -0.037 | 1.000 |
Posterior sample autocorrelations for each model parameter are shown in Output 44.10.8. The autocorrelation after 10 lags is negligible for all parameters, indicating good mixing in the Markov chain.
Output 44.10.8: Posterior Sample Autocorrelations
| Posterior Autocorrelations | ||||
|---|---|---|---|---|
| Parameter | Lag 1 | Lag 5 | Lag 10 | Lag 50 |
| Intercept | 0.3037 | 0.0152 | 0.0095 | -0.0170 |
| X1 | 0.3398 | 0.0025 | 0.0003 | 0.0052 |
| X2 | 0.3036 | 0.0061 | 0.0003 | -0.0062 |
| X3 | 0.3489 | 0.0190 | -0.0064 | -0.0210 |
| X4 | 0.2868 | 0.0213 | 0.0157 | -0.0107 |
| X5 | 0.2854 | 0.0108 | -0.0288 | -0.0012 |
| X6 | 0.3078 | 0.0230 | 0.0073 | 0.0062 |
The p-values for the Geweke test statistics shown in Output 44.10.9 all indicate convergence of the MCMC. See the section Assessing Markov Chain Convergence in Chapter 7: Introduction to Bayesian Analysis Procedures, for more information about convergence diagnostics and their interpretation.
Output 44.10.9: Geweke Diagnostic Statistics
The effective sample sizes for each parameter are shown in Output 44.10.10.
Output 44.10.10: Effective Sample Sizes
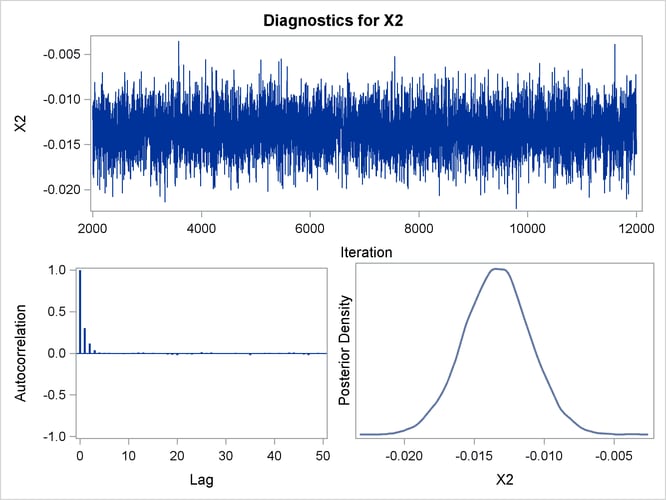
Trace, autocorrelation, and density plots for the seven model parameters are shown in Output 44.10.11 through Output 44.10.17. All indicate satisfactory convergence of the Markov chain.
Output 44.10.11: Diagnostic Plots for Intercept

Output 44.10.12: Diagnostic Plots for X1

Output 44.10.13: Diagnostic Plots for X2
Output 44.10.14: Diagnostic Plots for X3

Output 44.10.15: Diagnostic Plots for X4

Output 44.10.16: Diagnostic Plots for X5

Output 44.10.17: Diagnostic Plots for X6

In order to illustrate the use of an informative prior distribution, suppose that researchers expect that a unit increase
in body mass index (X1) will be associated with an increase in the mean number of nodes of between 10% and 20%, and they want to incorporate this
prior knowledge in the Bayesian analysis. For log-linear models, the mean and linear predictor are related by 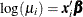 . If
. If X1 and
and X1 are two values of body mass index,
are two values of body mass index,  and
and  are the two mean values, and all other covariates remain equal for the two values of
are the two mean values, and all other covariates remain equal for the two values of X1, then
![\[ \frac{\mu _1}{\mu _2} = \exp (\beta (\Variable{X1}_1-\Variable{X1}_2)) \]](images/statug_genmod0728.png)
so that for a unit change in X1,
![\[ \frac{\mu _1}{\mu _2} = \exp (\beta ) \]](images/statug_genmod0729.png)
If  , then
, then  , or
, or  . This gives you guidance in specifying a prior distribution for the
. This gives you guidance in specifying a prior distribution for the  for body mass index. Taking the mean of the prior normal distribution to be the midrange of the values of
for body mass index. Taking the mean of the prior normal distribution to be the midrange of the values of  , and taking
, and taking  to be the extremes of the range, an
to be the extremes of the range, an  is the resulting prior distribution. The second analysis uses this informative normal prior distribution for the coefficient
of
is the resulting prior distribution. The second analysis uses this informative normal prior distribution for the coefficient
of X1 and uses independent noninformative normal priors with zero means and variances equal to  for the remaining model regression parameters.
for the remaining model regression parameters.
In the following BAYES statement, COEFFPRIOR=NORMAL(INPUT=NormalPrior) specifies the normal prior distribution for the regression coefficients with means and variances contained in the data set
NormalPrior.
An analysis is performed using PROC GENMOD to obtain Bayesian estimates of the regression coefficients by using the following SAS statements:
data NormalPrior; input _type_ $ Intercept X1-X6; datalines; Var 1e6 0.0005 1e6 1e6 1e6 1e6 1e6 Mean 0.0 0.1385 0.0 0.0 0.0 0.0 0.0 ;
proc genmod data=Liver; model Y = X1-X6 / dist=Poisson link=log; bayes seed=1 plots=none coeffprior=normal(input=NormalPrior); run;
The prior distributions for the regression parameters are shown in Output 44.10.18.
Output 44.10.18: Regression Coefficient Priors
Initial values for the MCMC are shown in Output 44.10.19. The initial values of the covariates are joint estimates of their posterior modes. The prior distribution for X1 is informative, so the initial value of X1 is further from the MLE than the rest of the covariates. Initial values for the rest of the covariates are close to their
MLEs, since noninformative prior distributions were specified for them.
Output 44.10.19: MCMC Initial Values and Seeds
Goodness-of-fit, summary, and interval statistics are shown in Output 44.10.20. Except for X1, the statistics shown in Output 44.10.20 are very similar to the previous statistics for noninformative priors shown in Output 44.10.4 through Output 44.10.7. The point estimate for X1 is now positive. This is expected because the prior distribution on 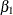 is quite informative. The distribution reflects the belief that the coefficient is positive. The
is quite informative. The distribution reflects the belief that the coefficient is positive. The  distribution places the majority of its probability density on positive values. As a result, the posterior density of
distribution places the majority of its probability density on positive values. As a result, the posterior density of 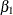 places more likelihood on positive values than in the noninformative case.
places more likelihood on positive values than in the noninformative case.
Output 44.10.20: Fit Statistics
| Posterior Summaries | ||||||
|---|---|---|---|---|---|---|
| Parameter | N | Mean | Standard Deviation |
Percentiles | ||
| 25% | 50% | 75% | ||||
| Intercept | 10000 | 2.1419 | 0.2157 | 1.9965 | 2.1430 | 2.2894 |
| X1 | 10000 | 0.0103 | 0.00684 | 0.00573 | 0.0104 | 0.0150 |
| X2 | 10000 | -0.0143 | 0.00233 | -0.0159 | -0.0142 | -0.0127 |
| X3 | 10000 | -0.00318 | 0.00218 | -0.00467 | -0.00314 | -0.00170 |
| X4 | 10000 | -0.2806 | 0.0800 | -0.3336 | -0.2793 | -0.2266 |
| X5 | 10000 | 0.3341 | 0.0832 | 0.2788 | 0.3341 | 0.3906 |
| X6 | 10000 | 0.2333 | 0.0826 | 0.1774 | 0.2325 | 0.2880 |
| Posterior Intervals | |||||
|---|---|---|---|---|---|
| Parameter | Alpha | Equal-Tail Interval | HPD Interval | ||
| Intercept | 0.050 | 1.7225 | 2.5574 | 1.7293 | 2.5632 |
| X1 | 0.050 | -0.00344 | 0.0235 | -0.00345 | 0.0234 |
| X2 | 0.050 | -0.0188 | -0.00970 | -0.0189 | -0.00980 |
| X3 | 0.050 | -0.00757 | 0.00108 | -0.00733 | 0.00121 |
| X4 | 0.050 | -0.4365 | -0.1200 | -0.4391 | -0.1256 |
| X5 | 0.050 | 0.1657 | 0.4966 | 0.1682 | 0.4987 |
| X6 | 0.050 | 0.0695 | 0.3959 | 0.0725 | 0.3981 |