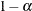The GENMOD Procedure
-
Overview
-
Getting Started
-
SyntaxPROC GENMOD StatementASSESS StatementBAYES StatementBY StatementCLASS StatementCODE StatementCONTRAST StatementDEVIANCE StatementEFFECTPLOT StatementESTIMATE StatementEXACT StatementEXACTOPTIONS StatementFREQ StatementFWDLINK StatementINVLINK StatementLSMEANS StatementLSMESTIMATE StatementMODEL StatementOUTPUT StatementProgramming StatementsREPEATED StatementSLICE StatementSTORE StatementSTRATA StatementVARIANCE StatementWEIGHT StatementZEROMODEL Statement
-
DetailsGeneralized Linear Models TheorySpecification of EffectsParameterization Used in PROC GENMODType 1 AnalysisType 3 AnalysisConfidence Intervals for ParametersF StatisticsLagrange Multiplier StatisticsPredicted Values of the MeanResidualsMultinomial ModelsZero-Inflated ModelsTweedie Distribution For Generalized Linear ModelsGeneralized Estimating EquationsAssessment of Models Based on Aggregates of ResidualsCase Deletion Diagnostic StatisticsBayesian AnalysisExact Logistic and Exact Poisson RegressionResponse Level OrderingMissing ValuesDisplayed Output for Classical AnalysisDisplayed Output for Bayesian AnalysisDisplayed Output for Exact AnalysisODS Table NamesODS Graphics
-
ExamplesLogistic RegressionNormal Regression, Log Link Gamma Distribution Applied to Life DataOrdinal Model for Multinomial DataGEE for Binary Data with Logit Link FunctionLog Odds Ratios and the ALR AlgorithmLog-Linear Model for Count DataModel Assessment of Multiple Regression Using Aggregates of ResidualsAssessment of a Marginal Model for Dependent DataBayesian Analysis of a Poisson Regression ModelExact Poisson RegressionTweedie Regression
- References
LSMESTIMATE Statement
-
LSMESTIMATE model-effect <'label'> values <divisor=n> <, …<'label'> values <divisor=n>></ options>;
The LSMESTIMATE statement provides a mechanism for obtaining custom hypothesis tests among least squares means.
Table 44.6 summarizes the options available in the LSMESTIMATE statement.
Table 44.6: LSMESTIMATE Statement Options
|
Option |
Description |
|---|---|
|
Construction and Computation of LS-Means |
|
|
Modifies covariate values in computing LS-means |
|
|
Computes separate margins |
|
|
Specifies a list of values to divide the coefficients |
|
|
Specifies the weighting scheme for LS-means computation as determined by a data set |
|
|
Tunes estimability checking |
|
|
Degrees of Freedom and p-values |
|
|
Determines the method for multiple-comparison adjustment of LS-means differences |
|
|
Determines the confidence level ( |
|
|
Performs one-sided, lower-tailed inference |
|
|
Adjusts multiple-comparison p-values further in a step-down fashion |
|
|
Specifies values under the null hypothesis for tests |
|
|
Performs one-sided, upper-tailed inference |
|
|
Statistical Output |
|
|
Constructs confidence limits for means and mean differences |
|
|
Displays the correlation matrix of LS-means |
|
|
Displays the covariance matrix of LS-means |
|
|
Prints the |
|
|
Prints the |
|
|
Produces a joint F or chi-square test for the LS-means and LS-means differences |
|
|
Requests graphs of means and mean comparisons |
|
|
Specifies the seed for computations that depend on random numbers |
|
|
Generalized Linear Modeling |
|
|
Specifies how to construct estimable functions with multinomial data |
|
|
Exponentiates and displays LS-means estimates |
|
|
Computes and displays estimates and standard errors of LS-means (but not differences) on the inverse linked scale |
|
For details about the syntax of the LSMESTIMATE statement, see the section LSMESTIMATE Statement in Chapter 19: Shared Concepts and Topics.