Language Reference

Nonlinear Optimization and Related Subroutines

Table 20.1: Nonlinear Optimization and Related Subroutines

Optimization Subroutines

Conjugate Gradient Optimization Method

CALL NLPCG( rc, xr, "fun", x0 <, opt, blc, tc, par, "ptit", "grd">);

Double Dogleg Optimization Method

CALL NLPDD( rc, xr, "fun", x0 <,opt, blc, tc, par, "ptit", "grd">);

Nelder-Mead Simplex Optimization Method

CALL NLPNMS( rc, xr, "fun", x0 <,opt, blc, tc, par, "ptit", "nlc">);

Newton-Raphson Optimization Method

CALL NLPNRA( rc, xr, "fun", x0 <,opt, blc, tc, par, "ptit", "grd", "hes">);

Newton-Raphson Ridge Optimization Method

CALL NLPNRR( rc, xr, "fun", x0 <,opt, blc, tc, par, "ptit", "grd", "hes">);

(Dual) Quasi-Newton Optimization Method

CALL NLPQN( rc, xr, "fun", x0 <,opt, blc, tc, par, "ptit", "grd", "nlc", "jacnlc">);

Quadratic Optimization Method

CALL NLPQUA( rc, xr, quad, x0 <,opt, blc, tc, par, "ptit", lin>);

Trust-Region Optimization Method

CALL NLPTR( rc, xr, "fun", x0 <,opt, blc, tc, par, "ptit", "grd", "hes">);

Least Squares Subroutines

Hybrid Quasi-Newton Least Squares Methods

CALL NLPHQN( rc, xr, "fun", x0, opt <,blc, tc, par, "ptit", "jac">);

Levenberg-Marquardt Least Squares Method

CALL NLPLM( rc, xr, "fun", x0, opt <,blc, tc, par, "ptit", "jac">);

Supplementary Subroutines

Approximate Derivatives by Finite Differences

CALL NLPFDD( f, g, h, "fun", x0 <,par, "grd">);

Feasible Point Subject to Constraints

CALL NLPFEA( xr, x0, blc <,par>);

Note: The names of the optional arguments can be used as keywords. For example, the following statements are equivalent:

  
    call nlpnrr(rc,xr,"fun",x0,,,ter,,,"grad"); 
    call nlpnrr(rc,xr,"fun",x0) tc=ter grd="grad";
 

All the optimization subroutines require at least two input arguments.

• The NLPQUA subroutine requires the quad matrix argument, which specifies the symmetric matrix G of the quadratic problem. The input can be dense or sparse. Other optimization subroutines require the fun module argument, which specifies an IML module that defines the objective function or functions. For least squares subroutines, the FUN module must return a column vector of length 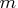that corresponds to the values of the 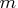functions 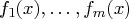, each evaluated at the point . For other subroutines, the FUN module must return the value of the objective function 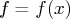evaluated at the point .
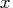• The argument x0 specifies a row vector that defines the number of parameters 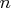. If x0 is a feasible point, it represents a starting point for the iterative optimization process. Otherwise, a linear programming algorithm is called at the start of each optimization subroutine to replace the input x0 by a feasible starting point.

The other arguments that can be used as input are described in the following list. As indicated in Table 20.1, not all input arguments apply to each subroutine.

Note that you can specify optional arguments with the keyword=argument syntax.

• The opt argument indicates an options vector that specifies details of the optimization process, such as particular updating techniques and whether the objective function is to be maximized instead of minimized. See the section "Options Vector" for details.
• The blc argument specifies a constraint matrix that defines lower and upper bounds for the 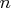parameters as well as general linear equality and inequality constraints. For details, see the section "Parameter Constraints".
• The tc argument specifies a vector of thresholds corresponding to the termination criteria tested in each iteration. See the section "Termination Criteria" for details.
• The par argument specifies a vector of control parameters that can be used to modify the algorithms if the default settings do not complete the optimization process successfully. For details, see the section "Control Parameters Vector".
• The "ptit" module argument specifies an IML module that replaces the subroutine used to print the iteration history and test the termination criteria. If the "ptit" module is specified, the matrix specified by the tc argument has no effect. See the section "Termination Criteria" for details.
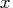• The "grd" module argument specifies an IML module that computes the gradient vector, , at a given input point . See the section "Objective Function and Derivatives" for details.
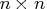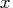• The "hes" module argument specifies an IML module that computes the Hessian matrix, , at a given input point . See the section "Objective Function and Derivatives" for details.
• The "jac" module argument specifies an IML module that computes the 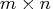Jacobian matrix, , of the 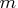least squares functions at a given input point 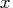. See the section "Objective Function and Derivatives" for details.
• The "nlc" module argument specifies an IML module that computes general equality and inequality constraints. This is the method by which nonlinear constraints must be specified. For details, see the section "Parameter Constraints".
• The "jacnlc" module argument specifies an IML module that computes the Jacobian matrix of first-order derivatives of the equality and inequality constraints specified by the NLC module. For details, see the section "Parameter Constraints".
• The lin argument specifies the linear part of the quadratic optimization problem. See the section "NLPQUA Call" for details.

The modules that can be used as input arguments for the subroutines ("fun," "grd," "hes," "jac," "ptit," "nlc," and "jacnlc") accept only a single input parameter . You can provide more input parameters for these modules by using the GLOBAL clause. See the section "Using the GLOBAL Clause" for an example.

All the optimization subroutines return the following results:

• The scalar return code rc indicates the reason for the termination of the optimization process. A return code rc  indicates successful termination corresponding to one of the specified termination criteria. A return code rc  indicates unsuccessful termination - that is, that the result xr is unreliable. See the section "Definition of Return Codes" for more details.
• The row vector xr, which has length 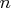, the number of parameters, contains the optimal point when rc .