Language Reference

NLPLM Call

calculates Levenberg-Marquardt least squares

CALL NLPLM( rc, xr, "fun", x0, opt, blc, tc, par, "ptit", "jac">);

See the section "Nonlinear Optimization and Related Subroutines" for a listing of all NLP subroutines. See Chapter 11 for a description of the inputs to and outputs of all NLP subroutines.

The NLPLM subroutine uses the Levenberg-Marquardt method, which is an efficient modification of the trust-region method for nonlinear least squares problems and is implemented as in Moré (1978). This is the recommended algorithm for small to medium least squares problems. Large least squares problems can often be processed more efficiently with other subroutines, such as the NLPCG and NLPQN methods. In each iteration, the NLPLM subroutine solves a quadratically constrained quadratic minimization problem that restricts the step to the boundary or interior of an -dimensional elliptical trust region.

The functions are computed by the module specified with the "fun" module argument. The Jacobian matrix, J, contains the first-order derivatives of the functions with respect to the parameters, as follows:

You can specify J with the "jac" module argument; otherwise, the subroutine will compute it with finite difference approximations. In each iteration, the subroutine computes the crossproduct of the Jacobian matrix, , to be used as an approximate Hessian.

Note: In least squares subroutines, you must set the first element of the opt vector to , the number of functions.

In addition to the standard iteration history, the NLPLM subroutine also prints the following information:

• Under the heading Iter, an asterisk (*) printed after the iteration number indicates that the computed Hessian approximation was singular and had to be ridged with a positive value.
• The heading lambda represents the Lagrange multiplier, 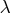. This has a value of zero when the optimum of the quadratic function approximation is inside the trust region, in which case a trust-region-scaled Newton step is performed. It is greater than zero when the optimum is at the boundary of the trust region, in which case the scaled Newton step is too long to fit in the trust region and a quadratically constrained optimization is done. Large values indicate optimization difficulties, and as in Gay (1983), a negative value indicates the special case of an indefinite Hessian matrix.
• The heading rho refers to 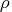, the ratio between the achieved and predicted difference in function values. Values that are much smaller than one indicate optimization difficulties. Values close to or larger than one indicate that the trust region radius can be increased.

See the section "Unconstrained Rosenbrock Function" for an example that uses the NLPLM subroutine to solve the unconstrained Rosenbrock problem.