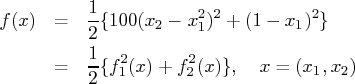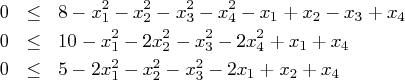Nonlinear Optimization Examples

Getting Started

Unconstrained Rosenbrock Function

The Rosenbrock function is defined as

$f(x) & = & \frac{1}2 \{ 100 (x_2 - x_1^2)^2 + (1 - x_1)^2 \} \ & = & \frac{1}2 \{ f_1^2(x) + f_2^2(x) \}, x = (x_1,x_2)$

The minimum function value

is at the point

The following code calls the NLPTR subroutine to solve the optimization problem:

  
    proc iml; 
       title 'Test of NLPTR subroutine: Gradient Specified'; 
       start F_ROSEN(x); 
          y1 = 10. * (x[2] - x[1] * x[1]); 
          y2 = 1. - x[1]; 
          f  = .5 * (y1 * y1 + y2 * y2); 
          return(f); 
       finish F_ROSEN; 
  
       start G_ROSEN(x); 
          g = j(1,2,0.); 
          g[1] = -200.*x[1]*(x[2]-x[1]*x[1]) - (1.-x[1]); 
          g[2] =  100.*(x[2]-x[1]*x[1]); 
          return(g); 
       finish G_ROSEN; 
  
       x = {-1.2 1.}; 
       optn = {0 2}; 
       call nlptr(rc,xres,"F_ROSEN",x,optn) grd="G_ROSEN"; 
       quit;

The NLPTR is a trust-region optimization method. The F_ROSEN module represents the Rosenbrock function, and the G_ROSEN module represents its gradient. Specifying the gradient can reduce the number of function calls by the optimization subroutine. The optimization begins at the initial point . For more information about the NLPTR subroutine and its arguments, see the section "NLPTR Call". For details about the options vector, which is given by the OPTN vector in the preceding code, see the section "Options Vector".

A portion of the output produced by the NLPTR subroutine is shown in Figure 11.1.

Trust Region Optimization

Without Parameter Scaling

CRP Jacobian Computed by Finite Differences

Parameter Estimates	2

Optimization Start
Active Constraints	0	Objective Function	12.1
Max Abs Gradient Element	107.8	Radius	1

Iteration		Restarts	Function Calls	Active Constraints		Objective Function	Objective Function Change	Max Abs Gradient Element	Lambda	Trust Region Radius
1		0	2	0		2.36594	9.7341	2.3189	0	1.000
2		0	5	0		2.05926	0.3067	5.2875	0.385	1.526
3		0	8	0		1.74390	0.3154	5.9934	0	1.086
.	.	.	.	.	.	.	.	.	.	.
.	.	.	.	.	.	.	.	.	.	.
.	.	.	.	.	.	.	.	.	.	.
22		0	31	0		1.3128E-16	6.96E-10	1.977E-7	0	0.00314

Optimization Results
Iterations	22	Function Calls	32
Hessian Calls	23	Active Constraints	0
Objective Function	1.312814E-16	Max Abs Gradient Element	1.9773384E-7
Lambda	0	Actual Over Pred Change	0
Radius	0.003140192

ABSGCONV convergence criterion satisfied.

Test of NLPTR subroutine: Gradient Specified

Optimization Results
Parameter Estimates
N	Parameter	Estimate	Gradient Objective Function
1	X1	1.000000	0.000000198
2	X2	1.000000	-0.000000105

Value of Objective Function = 1.312814E-16

Figure 11.1: NLPTR Solution to the Rosenbrock Problem

Since $f(x) = \frac{1}2 \{f_1^2(x) + f_2^2(x)\}$ , you can also use least squares techniques in this situation. The following code calls the NLPLM subroutine to solve the problem. The output is shown in Figure 11.2.

  
    proc iml; 
       title 'Test of NLPLM subroutine: No Derivatives'; 
       start F_ROSEN(x); 
         y = j(1,2,0.); 
         y[1] = 10. * (x[2] - x[1] * x[1]); 
         y[2] = 1. - x[1]; 
        return(y); 
       finish F_ROSEN; 
  
       x = {-1.2 1.}; 
       optn = {2 2}; 
       call nlplm(rc,xres,"F_ROSEN",x,optn); 
       quit;

Figure 11.2: NLPLM Solution Using the Least Squares Technique

The Levenberg-Marquardt least squares method, which is the method used by the NLPLM subroutine, is a modification of the trust-region method for nonlinear least squares problems. The F_ROSEN module represents the Rosenbrock function. Note that for least squares problems, the functions are specified as elements of a vector; this is different from the manner in which is specified for the other optimization techniques. No derivatives are specified in the preceding code, so the NLPLM subroutine computes finite-difference approximations. For more information about the NLPLM subroutine, see the section "NLPLM Call".

Constrained Betts Function

The linearly constrained Betts function (Hock & Schittkowski 1981) is defined as

The boundary constraints are

$2 \leq & x_1 & \leq 50 \ -50 \leq & x_2 & \leq 50$

The linear constraint is

$10x_1 - x_2 \geq 10$

The following code calls the NLPCG subroutine to solve the optimization problem. The infeasible initial point is specified, and a portion of the output is shown in Figure 11.3.

  
    proc iml; 
       title 'Test of NLPCG subroutine: No Derivatives'; 
       start F_BETTS(x); 
          f = .01 * x[1] * x[1] + x[2] * x[2] - 100.; 
          return(f); 
       finish F_BETTS; 
  
       con = {  2. -50.  .   ., 
               50.  50.  .   ., 
               10.  -1. 1. 10.}; 
       x = {-1. -1.}; 
       optn = {0 2}; 
       call nlpcg(rc,xres,"F_BETTS",x,optn,con); 
       quit;

The NLPCG subroutine performs conjugate gradient optimization. It requires only function and gradient calls. The F_BETTS module represents the Betts function, and since no module is defined to specify the gradient, first-order derivatives are computed by finite-difference approximations. For more information about the NLPCG subroutine, see the section "NLPCG Call". For details about the constraint matrix, which is represented by the CON matrix in the preceding code, see the section "Parameter Constraints".

NOTE:

Initial point was changed to be feasible for boundary and linear constraints.

Test of NLPTR subroutine: Gradient Specified

Optimization Start
Parameter Estimates
N	Parameter	Estimate	Gradient Objective Function	Lower Bound Constraint	Upper Bound Constraint
1	X1	6.800000	0.136000	2.000000	50.000000
2	X2	-1.000000	-2.000000	-50.000000	50.000000

Value of Objective Function = -98.5376

Linear Constraints
1	59.00000	:		10.0000	<=	+	10.0000	*	X1	-	1.0000	*	X2

Test of NLPTR subroutine: Gradient Specified

Conjugate-Gradient Optimization

Automatic Restart Update (Powell, 1977; Beale, 1972)

Gradient Computed by Finite Differences

Parameter Estimates	2
Lower Bounds	2
Upper Bounds	2
Linear Constraints	1

Figure 11.3: NLPCG Solution to Betts Problem

Optimization Start
Active Constraints	0	Objective Function	-98.5376
Max Abs Gradient Element	2

Iteration	Restarts	Function Calls	Active Constraints	Objective Function	Objective Function Change	Max Abs Gradient Element	Step Size	Slope of Search Direction
1	0	3	0	-99.54682	1.0092	0.1346	0.502	-4.018
2	1	7	1	-99.96000	0.4132	0.00272	34.985	-0.0182
3	2	9	1	-99.96000	1.851E-6	0	0.500	-74E-7

Optimization Results
Iterations	3	Function Calls	10
Gradient Calls	9	Active Constraints	1
Objective Function	-99.96	Max Abs Gradient Element	0
Slope of Search Direction	-7.398365E-6

ABSGCONV convergence criterion satisfied.

Test of NLPTR subroutine: Gradient Specified

Optimization Results
Parameter Estimates
N	Parameter	Estimate	Gradient Objective Function	Active Bound Constraint
1	X1	2.000000	0.040000	Lower BC
2	X2	-1.24028E-10	0

Value of Objective Function = -99.96

Linear Constraints Evaluated at Solution
1		10.00000	=	-10.0000	+	10.0000	*	X1	-	1.0000	*	X2

Figure 11.3: (continued)

Since the initial point is infeasible, the subroutine first computes a feasible starting point. Convergence is achieved after three iterations, and the optimal point is given to be with an optimal function value of . For more information about the printed output, see the section "Printing the Optimization History".

Rosen-Suzuki Problem

The Rosen-Suzuki problem is a function of four variables with three nonlinear constraints on the variables. It is taken from problem 43 of Hock and Schittkowski (1981). The objective function is

The nonlinear constraints are

$0 & \leq & 8 - x_1^2 - x_2^2 - x_3^2 - x_4^2 - x_1 + x_2 - x_3 + x_4 \ 0 & \leq... ... 2x_4^2 + x_1 + x_4 \ 0 & \leq & 5 - 2x_1^2 - x_2^2 - x_3^2 - 2x_1 + x_2 + x_4$

Since this problem has nonlinear constraints, only the NLPQN and NLPNMS subroutines are available to perform the optimization. The following code solves the problem with the NLPQN subroutine:

  
    proc iml; 
       start F_HS43(x); 
          f = x*x` + x[3]*x[3] - 5*(x[1] + x[2]) - 21*x[3] + 7*x[4]; 
          return(f); 
       finish F_HS43; 
       start C_HS43(x); 
          c = j(3,1,0.); 
          c[1] = 8 - x*x` - x[1] + x[2] - x[3] + x[4]; 
          c[2] = 10 - x*x` - x[2]*x[2] - x[4]*x[4] + x[1] + x[4]; 
          c[3] = 5 - 2.*x[1]*x[1] - x[2]*x[2] - x[3]*x[3] 
                   - 2.*x[1] + x[2] + x[4]; 
          return(c); 
       finish C_HS43; 
       x = j(1,4,1); 
       optn= j(1,11,.); optn[2]= 3; optn[10]= 3; optn[11]=0; 
       call nlpqn(rc,xres,"F_HS43",x,optn) nlc="C_HS43";

The F_HS43 module specifies the objective function, and the C_HS43 module specifies the nonlinear constraints. The OPTN vector is passed to the subroutine as the OPT input argument. See the section "Options Vector" for more information. The value of OPTN[10] represents the total number of nonlinear constraints, and the value of OPTN[11] represents the number of equality constraints. In the preceding code, OPTN[10]=3 and OPTN[11]=0, which indicate that there are three constraints, all of which are inequality constraints. In the subroutine calls, instead of separating missing input arguments with commas, you can specify optional arguments with keywords, as in the CALL NLPQN statement in the preceding code. For details about the CALL NLPQN statement, see the section "NLPQN Call".

The initial point for the optimization procedure is , and the optimal point is , with an optimal function value of . Part of the output produced is shown in Figure 11.4.

Dual Quasi-Newton Optimization

Modified VMCWD Algorithm of Powell (1978, 1982)

Dual Broyden - Fletcher - Goldfarb - Shanno Update (DBFGS)

Lagrange Multiplier Update of Powell(1982)

Gradient Computed by Finite Differences

Jacobian Nonlinear Constraints Computed by Finite Differences

Parameter Estimates	4
Nonlinear Constraints	3

Optimization Start
Objective Function	-19	Maximum Constraint Violation	0
Maximum Gradient of the Lagran Func	17

Iteration	Restarts	Function Calls	Objective Function	Maximum Constraint Violation	Predicted Function Reduction	Step Size	Maximum Gradient Element of the Lagrange Function
1	0	2	-41.88007	1.8988	13.6803	1.000	5.647
2	0	3	-48.83264	3.0280	9.5464	1.000	5.041
3	0	4	-45.33515	0.5452	2.6179	1.000	1.061
4	0	5	-44.08667	0.0427	0.1732	1.000	0.0297
5	0	6	-44.00011	0.000099	0.000218	1.000	0.00906
6	0	7	-44.00001	2.573E-6	0.000014	1.000	0.00219
7	0	8	-44.00000	9.118E-8	5.097E-7	1.000	0.00022

Figure 11.4: Solution to the Rosen-Suzuki Problem by the NLPQN Subroutine

Optimization Results
Iterations	7	Function Calls	9
Gradient Calls	9	Active Constraints	2
Objective Function	-44.00000026	Maximum Constraint Violation	9.1176306E-8
Maximum Projected Gradient	0.0002265341	Value Lagrange Function	-44
Maximum Gradient of the Lagran Func	0.00022158	Slope of Search Direction	-5.097332E-7

FCONV2 convergence criterion satisfied.

WARNING:

The point x is feasible only at the LCEPSILON= 1E-7 range.

Test of NLPTR subroutine: Gradient Specified

Optimization Results
Parameter Estimates
N	Parameter	Estimate	Gradient Objective Function	Gradient Lagrange Function
1	X1	-0.000001248	-5.000002	-0.000012804
2	X2	1.000027	-2.999945	0.000222
3	X3	1.999993	-13.000027	-0.000054166
4	X4	-1.000003	4.999995	-0.000020681

Value of Objective Function = -44.00000026

Value of Lagrange Function = -44

Figure 11.4: (continued)

In addition to the standard iteration history, the NLPQN subroutine includes the following information for problems with nonlinear constraints:

CONMAX is the maximum value of all constraint violations.
PRED is the value of the predicted function reduction used with the GTOL and FTOL2 termination criteria.
ALFA is the step size 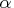$\alpha$ of the quasi-Newton step.
LFGMAX is the maximum element of the gradient of the Lagrange function.

Top of Page