| Language Reference |
NLPQN Call
nonlinear optimization by quasi-Newton method
- CALL NLPQN( rc, xr, "fun", x0 <,opt, blc, tc, par, "ptit",
- "grd", "nlc", "jacnlc">);
See the section "Nonlinear Optimization and Related Subroutines" for a listing of all NLP subroutines. See Chapter 11 for a description of the inputs to and outputs of all NLP subroutines.
The NLPQN subroutine uses (dual) quasi-Newton optimization techniques, and it is one of the two subroutines available that can solve problems with nonlinear constraints. These techniques work well for medium to moderately large optimization problems where the objective function and the gradient are much faster to compute than the Hessian matrix. The NLPQN subroutine does not need to compute second-order derivatives, but it generally requires more iterations than the techniques that compute second-order derivatives.
The two categories of problems solved by the NLPQN subroutine are unconstrained or linearly constrained problems and nonlinearly constrained problems. Unconstrained or linearly constrained problems do not use the "nlc" or "jacnlc" module arguments, whereas nonlinearly constrained problems use the arguments to specify the nonlinear constraints and the Jacobian matrix of their first-order derivatives, respectively.
The type of optimization problem specified determines the algorithm that the subroutine invokes. The algorithms are very different, and they use different sets of termination criteria. For more details, see the section "Termination Criteria".
Unconstrained or Linearly Constrained QN Optimization
The NLPQN subroutine invokes this algorithm if you do not specify the "nlc" argument. Using the fourth element of the opt argument, you can specify two update formulas for either the original quasi-Newton algorithm or the dual quasi-Newton algorithm, as indicated in the following table:| Value of opt[4] | Update Method |
| 1 | Dual Broyden, Fletcher, Goldfarb, and Shanno (DBFGS) update of the Cholesky factor of the Hessian matrix. This is the default. |
| 2 | Dual Davidon, Fletcher, and Powell (DDFP) update of the Cholesky factor of the Hessian matrix. |
| 3 | Original Broyden, Fletcher, Goldfarb, and Shanno (BFGS) update of the inverse Hessian matrix. |
| 4 | Original Davidon, Fletcher, and Powell (DFP) update of the inverse Hessian matrix. |
In each iteration, a line search is performed along the search direction to find an approximate optimum of the objective function. The default line-search method uses quadratic interpolation and cubic extrapolation to obtain a step size that satisfies the Goldstein conditions. One of the Goldstein conditions can be violated if the feasible region defines an upper limit of the step size. Violating the left-side Goldstein condition can affect the positive definiteness of the quasi-Newton update. In these cases, either the update is skipped or the iterations are restarted with an identity matrix resulting in the steepest descent or ascent search direction. You can specify line-search algorithms different from the default method with the fifth element of the opt argument.
Note: In SAS 6.08, the DBFGS and DDFP updates were implemented with the NLPDQN subroutine. In SAS 6.09 and in later releases, these updates are specified with the NLPQN subroutine, and the NLPDQN subroutine is not permitted.
The following statements invoke the NLPQN subroutine to solve the Rosenbrock problem (see the section "Unconstrained Rosenbrock Function"):
start F_ROSEN(x);
y1 = 10. * (x[2] - x[1] * x[1]);
y2 = 1. - x[1];
f = .5 * (y1 * y1 + y2 * y2);
return(f);
finish F_ROSEN;
x = {-1.2 1.};
optn = {0 2 . 2};
call nlpqn(rc,xr,"F_ROSEN",x,optn);
Since OPTN
- The heading alpha is the step size,
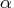 , computed with the line-search algorithm.
, computed with the line-search algorithm.
- The heading slope refers to
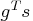 , the slope of the
search direction at the current parameter iterate
, the slope of the
search direction at the current parameter iterate 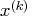 .
For minimization, this value should
be significantly smaller than zero.
Otherwise, the line-search algorithm has difficulty
reducing the function value sufficiently.
.
For minimization, this value should
be significantly smaller than zero.
Otherwise, the line-search algorithm has difficulty
reducing the function value sufficiently.
Optimization Start
Parameter Estimates
Gradient
Objective
N Parameter Estimate Function
1 X1 -1.200000 -107.799989
2 X2 1.000000 -43.999999
Value of Objective Function = 12.1
Dual Quasi-Newton Optimization
Dual Davidon - Fletcher - Powell Update (DDFP)
Gradient Computed by Finite Differences
Parameter Estimates 2
Optimization Start
Active Constraints 0 Objective Function 12.1
Max Abs Gradient Element 107.79998927
Function Active Objective
Iter Restarts Calls Constraints Function
1 0 4 0 2.06405
2 0 7 0 1.92035
3 0 10 0 1.78089
4 0 13 0 1.33331
5 0 17 0 1.13400
6 0 22 0 0.93915
7 0 24 0 0.84821
8 0 30 0 0.54334
9 0 32 0 0.46593
10 0 37 0 0.35322
12 0 41 0 0.20282
12 0 41 0 0.20282
13 0 46 0 0.11714
14 0 51 0 0.07149
15 0 53 0 0.04746
16 0 58 0 0.02759
17 0 60 0 0.01625
18 0 62 0 0.00475
19 0 66 0 0.00167
20 0 70 0 0.0005952
21 0 72 0 0.0000771
23 0 78 0 2.39914E-8
23 0 78 0 2.39914E-8
24 0 80 0 5.0936E-11
25 0 119 0 3.9538E-11
Objective Max Abs Slope of
Function Gradient Step Search
Iter Change Element Size Direction
1 10.0359 0.7917 0.0340 -628.8
2 0.1437 8.6301 6.557 -0.0363
3 0.1395 11.0943 8.193 -0.0288
4 0.4476 7.6069 33.376 -0.0269
5 0.1993 0.9386 15.438 -0.0260
6 0.1948 3.5290 11.537 -0.0233
7 0.0909 4.8308 8.124 -0.0193
8 0.3049 4.1770 35.143 -0.0186
9 0.0774 0.9479 8.708 -0.0178
10 0.1127 2.5981 10.964 -0.0147
11 0.0894 3.3028 13.590 -0.0121
12 0.0610 0.6451 10.000 -0.0116
13 0.0857 1.6603 11.395 -0.0102
14 0.0456 2.4050 11.559 -0.0074
15 0.0240 0.5628 6.868 -0.0071
16 0.0199 1.3282 5.365 -0.0055
17 0.0113 1.9246 5.882 -0.0035
18 0.0115 0.6357 8.068 -0.0032
19 0.00307 0.4810 2.336 -0.0022
20 0.00108 0.6043 3.287 -0.0006
21 0.000518 0.0289 2.329 -0.0004
22 0.000075 0.0365 1.772 -0.0001
23 1.897E-6 0.00158 1.159 -331E-8
24 2.394E-8 0.000016 0.967 -46E-9
25 1.14E-11 7.962E-7 1.061 -19E-13
Optimization Results
Iterations 25 Function Calls 120
Gradient Calls 107 Active Constraints 0
Objective Function 3.953804E-11 Max Abs Gradient Element 7.9622469E-7
Slope of Search Direction -1.88032E-12
ABSGCONV convergence criterion satisfied.
Optimization Results
Parameter Estimates
Gradient
Objective
N Parameter Estimate Function
1 X1 0.999991 -0.000000796
2 X2 0.999982 0.000000430
Value of Objective Function = 3.953804E-11
Nonlinearly Constrained QN Optimization
The algorithm used for nonlinearly constrained quasi-Newton optimization is an efficient modification of Powell's (1978a, 1982b) Variable Metric Constrained WatchDog (VMCWD) algorithm. A similar but older algorithm (VF02AD) is part of the Harwell library. Both the VMCWD and VF02AD algorithms use Fletcher's VE02AD algorithm, which is also part of the Harwell library, for positive definite quadratic programming. This NLPQN implementation uses a quadratic programming subroutine that updates and downdates the Cholesky factor when the active set changes (refer to Gill et al. 1984). The nonlinear NLPQN algorithm is not a feasible point algorithm, and the value of the objective function is not required to decrease monotonically. Instead, the algorithm tries to reduce a linear combination of objective function and constraint violations.The following are similarities and differences between this algorithm and Powell's VMCWD algorithm:
- You can use the sixth element of the opt argument
to modify the algorithm used by the NLPQN subroutine.
If you specify opt
![[6]=2](images/langref_langrefeq806.gif) , which is the default,
the evaluation of the Lagrange vector
, which is the default,
the evaluation of the Lagrange vector 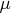 is
performed the same way as described in Powell (1982b).
Note, however, that the VMCWD program seems to have a bug
in the implementation of formula (4.4) in Powell (1982b).
If you specify opt
is
performed the same way as described in Powell (1982b).
Note, however, that the VMCWD program seems to have a bug
in the implementation of formula (4.4) in Powell (1982b).
If you specify opt![[6]=1](images/langref_langrefeq808.gif) , the
original update of
, the
original update of 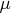 used in the VF02AD
algorithm in Powell (1978a) is performed.
used in the VF02AD
algorithm in Powell (1978a) is performed.
- Instead of updating an approximate Hessian matrix, this algorithm uses the dual BFGS or dual DFP update that updates the Cholesky factor of an approximate Hessian. If the condition of the updated matrix gets too bad, a restart is done with a positive diagonal matrix. At the end of the first iteration after each restart, the Cholesky factor is scaled.
- The Cholesky factor is loaded into the
quadratic programming subroutine, which
ensures positive definiteness of the problem.
During the quadratic programming step, the
Cholesky factor of the projected Hessian matrix
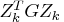 is updated simultaneously with
is updated simultaneously with
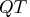 decomposition when the active set changes.
Refer to Gill et al. (1984) for more information.
decomposition when the active set changes.
Refer to Gill et al. (1984) for more information.
- The line-search strategy is very similar to that
of Powell's algorithm, but this algorithm does
not call for derivatives during the line search.
For that reason, this algorithm generally needs
fewer derivative calls than function calls,
whereas the VMCWD algorithm always requires the
same number of derivative calls as function calls.
Also, Powell's line-search method sometimes uses
steps that are too long during the early iterations.
In those cases, you can use the second element
of the par argument to restrict the step
length
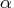 in the first five iterations.
See the section "Control Parameters Vector" for more details.
in the first five iterations.
See the section "Control Parameters Vector" for more details.
- The watchdog strategy is also similar to that of Powell's algorithm. However, this algorithm does not return automatically after a fixed number of iterations to a previous, more optimal point. A return to such a point is further delayed if the observed function reduction is close to the expected function reduction of the quadratic model.
- Although Powell's termination criterion, the FTOL2 criterion, can still be used, the NLPQN implementation uses, by default, two other termination criteria (GTOL and ABSGTOL).
Note: You must specify the total number of constraints with the tenth element of the opt argument, and if there are any equality constraints, you must specify that number,
The nonlinear NLPQN algorithm requires the Jacobian matrix of the first-order derivatives of the
You can specify two update formulas with the fourth element of the opt argument as indicated in the following table:
| Value of opt[4] | Update Method |
| 1 | Dual Broyden, Fletcher, Goldfarb, and Shanno (DBFGS) update of the Cholesky factor of the Hessian matrix. This is the default. |
| 2 | Dual Davidon, Fletcher, and Powell (DDFP) update of the Cholesky factor of the Hessian matrix. |
This algorithm uses its own line-search technique. None of the options and parameters that control the line search in the other algorithms apply in the nonlinear NLPQN algorithm, with the exception of the second element of the par vector, which can be used to restrict the length of the step size in the first five iterations.
See Example 11.8 for an example where you need to specify a value for the second element of the par argument. The values of the fourth, fifth, and sixth elements of the par vector, which control the processing of linear and boundary constraints, are valid only for the quadratic programming subroutine used in each iteration of the NLPQN call. For a simple example of the NLPQN subroutine, see the section "Rosen-Suzuki Problem".
Copyright © 2009 by SAS Institute Inc., Cary, NC, USA. All rights reserved.