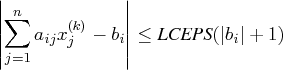| Nonlinear Optimization Examples |
Control Parameters Vector
For all optimization and least squares subroutines,
the input argument par specifies a vector of
parameters that control the optimization process.
For the NLPFDD and NLPFEA subroutines, the
par argument is defined differently.
For each element of the par vector there
exists a default value, and if you specify
a missing value, the default is used.
Table 11.5 summarizes the uses of the par
argument for the optimization and least squares subroutines.
Table 11.5: Summary of the Control Parameters Vector
|
Index
|
Description
|
| 1 | specifies the singularity criterion (SINGULAR) |
| 2 | specifies the initial step length or trust-region radius |
| 3 | specifies the range for active (violated) constraints (LCEPS) |
| 4 | specifies the Lagrange multiplier threshold for constraints
(LCDEACT) |
| 5 | specifies a criterion to determine linear dependence of
constraints (LCSING) |
| 6 | specifies the required accuracy of the line-search algorithms
(LSPRECISION) |
| 7 | reduces the line-search step size in successive iterations
(DAMPSTEP) |
| 8 | specifies the number of accurate digits used in evaluating
the objective function (FDIGITS) |
| 9 | specifies the number of accurate digits used in evaluating
the nonlinear constraints (CDIGITS) |
| 10 | specifies a scalar factor for the diagonal of the initial
Hessian (DIAHES) |
- par[1]
specifies the singularity criterion for the
decomposition of the Hessian matrix (SINGULAR).
The value must be between zero and one, and
the default is par
![[1]=](images/nonlinearoptexpls_nonlinearoptexplseq213.gif) 1E-8.
1E-8.
par[2]
specifies different features depending
on the subroutine in which it is used.
In the NLPNMS subroutine, it defines
the size of the start simplex.
For the original Nelder-Mead simplex algorithm, the
default value is par![[2]=1](images/nonlinearoptexpls_nonlinearoptexplseq214.gif) ; for the COBYLA
algorithm, the default is par
; for the COBYLA
algorithm, the default is par![[2]=0.5](images/nonlinearoptexpls_nonlinearoptexplseq215.gif) .
In the NLPCG, NLPQN, and NLPHQN subroutines,
the par[2] argument specifies an upper
bound for the initial step length for the
line search during the first five iterations.
The default initial step length is par
.
In the NLPCG, NLPQN, and NLPHQN subroutines,
the par[2] argument specifies an upper
bound for the initial step length for the
line search during the first five iterations.
The default initial step length is par![[2]=1](images/nonlinearoptexpls_nonlinearoptexplseq214.gif) .
In the NLPTR, NLPDD, and NLPLM subroutines,
the par[2] argument specifies a factor
for the initial trust-region radius,
.
In the NLPTR, NLPDD, and NLPLM subroutines,
the par[2] argument specifies a factor
for the initial trust-region radius, 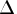 .
For highly nonlinear functions, the default step length
or trust-region radius can result in arithmetic overflows.
In that case, you can specify stepwise decreasing values
of par[2], such as par[2]=1E-1, par[2]=1E-2,
par[2]=1E-4, until the subroutine starts to iterate successfully.
.
For highly nonlinear functions, the default step length
or trust-region radius can result in arithmetic overflows.
In that case, you can specify stepwise decreasing values
of par[2], such as par[2]=1E-1, par[2]=1E-2,
par[2]=1E-4, until the subroutine starts to iterate successfully.
par[3]
specifies the range (LCEPS) for active
and violated linear constraints.
The 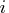 th constraint is considered an active
constraint if the point
th constraint is considered an active
constraint if the point 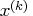 satisfies the condition
satisfies the condition
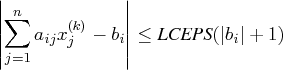
where LCEPS is the value of par[3]
and  and
and  are defined as in
the section "Parameter Constraints".
Otherwise, the constraint
are defined as in
the section "Parameter Constraints".
Otherwise, the constraint  is either an inactive
inequality or a violated inequality or equality constraint.
The default is par
is either an inactive
inequality or a violated inequality or equality constraint.
The default is par![[3]=](images/nonlinearoptexpls_nonlinearoptexplseq218.gif) 1E-8.
During the optimization process, the introduction
of rounding errors can force the subroutine to
increase the value of par[3] by a power of 10,
but the value never becomes larger than 1E-3.
1E-8.
During the optimization process, the introduction
of rounding errors can force the subroutine to
increase the value of par[3] by a power of 10,
but the value never becomes larger than 1E-3.
par[4]
specifies a threshold (LCDEACT) for the Lagrange
multiplier that decides whether an active inequality
constraint must remain active or can be deactivated.
For maximization, par[4] must be positive, and for
minimization, par[4] must be negative.
The default is
![{par}[4] = +- \min (0.01, \max ( 0.1 x {absgtol}, 0.001 x {gmax}^{(k)} ) )](images/nonlinearoptexpls_nonlinearoptexplseq219.gif)
where the positive value is for maximization
and the negative value is for minimization.
ABSGTOL is the value of the absolute gradient
criterion, and 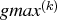 is the
maximum absolute element of the gradient,
is the
maximum absolute element of the gradient, 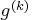 ,
or the projected gradient,
,
or the projected gradient, 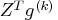 .
.
par[5]
specifies a criterion (LCSING) used in the update of the
QR decomposition that decides whether an active constraint
is linearly dependent on a set of other active constraints.
The default is par![[5]=](images/nonlinearoptexpls_nonlinearoptexplseq176.gif) 1E-8.
As the value of par[5] increases, more active
constraints are recognized as being linearly dependent.
If the value of par[5] is larger than 0.1, it is
reset to 0.1, and if it is negative, it is reset to zero.
1E-8.
As the value of par[5] increases, more active
constraints are recognized as being linearly dependent.
If the value of par[5] is larger than 0.1, it is
reset to 0.1, and if it is negative, it is reset to zero.
par[6]
specifies the degree of accuracy (LSPRECISION) that should
be obtained by the second or third line-search algorithm.
This argument can be used with the NLPCG, NLPHQN,
and NLPNRA algorithms and with the NLPQN algorithm
if the "nlc" argument is specified.
Usually, an imprecise line search is computationally
inexpensive and successful, but for more difficult
optimization problems, a more precise and
time consuming line search can be necessary.
Refer to Fletcher (1987) for details.
If you have numerical problems, you should
decrease the value of the par[6]
argument to obtain a more precise line search.
The default values are given in the following table.
|
Subroutine
|
Update Method
|
Default value
|
| NLPCG | All | par[6] = 0.1 |
| NLPHQN | DBFGS | par[6] = 0.1 |
| NLPHQN | DDFP | par[6] = 0.06 |
| NLPNRA | No update | par[6] = 0.9 |
| NLPQN | BFGS, DBFGS | par[6] = 0.4 |
| NLPQN | DFP, DDFP | par[6] = 0.06 |
par[7]
specifies a scalar factor (DAMPSTEP) that can be used to
reduce the step size in each of the first five iterations.
In each of these iterations, the starting step size,
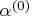 , can be no larger than the value of
par[7] times the step size obtained by the
line-search algorithm in the previous iteration.
If par[7] is missing or ifpar[7]=0, which is the
default, the starting step size in iteration
, can be no larger than the value of
par[7] times the step size obtained by the
line-search algorithm in the previous iteration.
If par[7] is missing or ifpar[7]=0, which is the
default, the starting step size in iteration 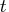 is computed as a function of the function change
from the former iteration,
is computed as a function of the function change
from the former iteration, 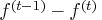 .
If the computed value is outside the interval
.
If the computed value is outside the interval
![[0.1,10.0]](images/nonlinearoptexpls_nonlinearoptexplseq226.gif) , it is moved to the next endpoint.
You can further restrict the starting step size in the
first five iterations with the par[2] argument.
, it is moved to the next endpoint.
You can further restrict the starting step size in the
first five iterations with the par[2] argument.
par[8]
specifies the number of accurate digits (FDIGITS)
used to evaluate the objective function.
The default is 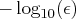 ,
where
,
where 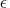 is the machine precision,
and fractional values are permitted.
This value is used to compute the step size
is the machine precision,
and fractional values are permitted.
This value is used to compute the step size
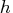 for finite-difference derivatives and the
default value for the FTOL termination criterion.
for finite-difference derivatives and the
default value for the FTOL termination criterion.
par[9]
specifies the number of accurate digits
(CDIGITS) used to evaluate the nonlinear
constraint functions of the "nlc" module.
The default is 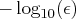 , where
, where 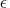 is
the machine precision, and fractional values are permitted.
The value is used to compute the step size
is
the machine precision, and fractional values are permitted.
The value is used to compute the step size
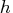 for finite-difference derivatives.
If first-order derivatives are specified by the
"jacnlc" module, the par[9] argument is ignored.
for finite-difference derivatives.
If first-order derivatives are specified by the
"jacnlc" module, the par[9] argument is ignored.
par[10]
specifies a scalar factor (DIAHES) for the
diagonal of the initial Hessian approximation.
This argument is available in the
NLPDD, NLPHQN, and NLPQN subroutines.
If the opt[7] argument is not specified,
the initial Hessian approximation is a multiple
of the identity matrix determined by the
magnitude of the initial gradient 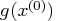 .
The value of the par[10] argument is used to
specify
.
The value of the par[10] argument is used to
specify ![{par}[10] x i\;](images/nonlinearoptexpls_nonlinearoptexplseq229.gif) for
the initial Hessian in the quasi-Newton algorithm.
for
the initial Hessian in the quasi-Newton algorithm.
Copyright © 2009 by SAS Institute Inc., Cary, NC, USA. All rights reserved.
![[1]=](images/nonlinearoptexpls_nonlinearoptexplseq213.gif) 1E-8.
1E-8.