| Language Reference |
NLPNRR Call
nonlinear optimization by Newton-Raphson ridge method
- CALL NLPNRR( rc, xr, "fun", x0 <,opt, blc, tc, par, "ptit", "grd", "hes">);
See the section "Nonlinear Optimization and Related Subroutines" for a listing of all NLP subroutines. See Chapter 11 for a description of the inputs to and outputs of all NLP subroutines.
The NLPNRR algorithm uses a pure Newton step when both the Hessian is positive definite and the Newton step successfully reduces the value of the objective function. Otherwise, a multiple of the identity matrix is added to the Hessian matrix.
The subroutine uses the gradient ![]() and the Hessian matrix
and the Hessian matrix
![]() ,
and it requires continuous first- and second-order derivatives
of the objective function inside the feasible region.
,
and it requires continuous first- and second-order derivatives
of the objective function inside the feasible region.
Note that using only function calls to compute finite difference
approximations for second-order derivatives can be computationally
very expensive and can contain significant rounding errors.
If you use the "grd" input argument to specify
a module that computes first-order derivatives
analytically, you can reduce drastically the
computation time for numerical second-order derivatives.
The computation of the finite difference approximation
for the Hessian matrix generally uses only ![]() calls of the module that specifies the gradient.
calls of the module that specifies the gradient.
The NLPNRR method performs well for small to medium-sized problems, and it does not need many function, gradient, and Hessian calls. However, if the gradient is not specified analytically by using the "grd" module argument, or if the computation of the Hessian module specified with the "hes" argument is computationally expensive, one of the (dual) quasi-Newton or conjugate gradient algorithms might be more efficient.
In addition to the standard iteration history, the NLPNRR subroutine prints the following information:
- The heading ridge refers to the value of the nonnegative ridge parameter. A value of zero indicates that a Newton step is performed. A value greater than zero indicates either that the Hessian approximation is zero or that the Newton step fails to reduce the optimization criterion. A large value can indicate optimization difficulties.
- The heading rho refers to
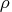 , the ratio of the
achieved difference in function values and the predicted
difference, based on the quadratic function approximation.
A value that is much smaller than one
indicates possible optimization difficulties.
, the ratio of the
achieved difference in function values and the predicted
difference, based on the quadratic function approximation.
A value that is much smaller than one
indicates possible optimization difficulties.
The following statements invoke the NLPNRR subroutine to solve the constrained Betts optimization problem (see the section "Constrained Betts Function"). The iteration history follows.
start F_BETTS(x);
f = .01 * x[1] * x[1] + x[2] * x[2] - 100.;
return(f);
finish F_BETTS;
con = { 2. -50. . .,
50. 50. . .,
10. -1. 1. 10.};
x = {-1. -1.};
optn = {0 2};
call nlpnrr(rc,xres,"F_BETTS",x,optn,con);
quit;
Optimization Start
Parameter Estimates
Gradient Lower Upper
Objective Bound Bound
N Parameter Estimate Function Constraint Constraint
1 X1 6.800000 0.136000 2.000000 50.000000
2 X2 -1.000000 -2.000000 -50.000000 50.000000
Value of Objective Function = -98.5376
Linear Constraints
1 59.00000 : 10.0000 <= + 10.0000 * X1 - 1.0000 * X2
Newton-Raphson Ridge Optimization
Without Parameter Scaling
Gradient Computed by Finite Differences
CRP Jacobian Computed by Finite Differences
Parameter Estimates 2
Lower Bounds 2
Upper Bounds 2
Linear Constraints 1
Optimization Start
Active Constraints 0 Objective Function -98.5376
Max Abs Gradient Element 2
Function Active Objective
Iter Restarts Calls Constraints Function
1 0 2 1 -99.87337
2 0 3 1 -99.96000
3 0 4 1 -99.96000
Ratio
Actual
Objective Max Abs and
Function Gradient Predicted
Iter Change Element Ridge Change
1 1.3358 0.5887 0 0.706
2 0.0866 0.000040 0 1.000
3 4.07E-10 0 0 1.014
Optimization Results
Iterations 3 Function Calls 5
Hessian Calls 4 Active Constraints 1
Objective Function -99.96 Max Abs Gradient Element 0
Ridge 0 Actual Over Pred Change 1.0135158294
GCONV convergence criterion satisfied.
Optimization Results
Parameter Estimates
Gradient Active
Objective Bound
N Parameter Estimate Function Constraint
1 X1 2.000000 0.040000 Lower BC
2 X2 0.000000134 0
Value of Objective Function = -99.96
Linear Constraints Evaluated at Solution
1 10.00000 = -10.0000 + 10.0000 * X1 - 1.0000 * X2
Copyright © 2009 by SAS Institute Inc., Cary, NC, USA. All rights reserved.