Language Reference: NLPTR Call :: SAS/IML(R) 9.2 User's Guide

Language Reference

NLPTR Call

nonlinear optimization by trust-region method

CALL NLPTR( rc, xr, "fun", x0 <,opt, blc, tc, par, "ptit", "grd", "hes">);

See the section "Nonlinear Optimization and Related Subroutines" for a listing of all NLP subroutines. See Chapter 11 for a description of the inputs to and outputs of all NLP subroutines.

The NLPTR subroutine is a trust-region method that uses the gradient $g^{(k)} = \nabla f(x^{(k)})$ and Hessian matrix $g^{(k)} = \nabla^2 f(x^{(k)})$ . It requires that the objective function

has continuous first- and second-order derivatives inside the feasible region.

The

Hessian matrix G contains the second derivatives of the objective function

with respect to the parameters

as follows:

$g(x) = \nabla^2 f(x) = ( \frac{\partial^2 f}{\partial x_j \partial x_k} )$

The trust-region method works by optimizing a quadratic approximation to the nonlinear objective function within a hyperelliptic trust region. This trust region has a radius, $\delta$ , that constrains the step size corresponding to the quality of the quadratic approximation. The method is implemented by using Dennis, Gay, and Welsch (1981), Gay (1983), and Moré and Sorensen (1983).

Note that finite difference approximations for second-order derivatives using only function calls are computationally very expensive. If you specify first-order derivatives analytically with the "grd" module argument, you can drastically reduce the computation time for numerical second-order derivatives. Computing the finite difference approximation for the Hessian matrix G generally uses only calls of the module that computes the gradient analytically.

The NLPTR method performs well for small to medium-sized problems and does not need many function, gradient, and Hessian calls. However, if the gradient is not specified analytically by using the "grd" argument or if the computation of the Hessian module, as specified by the "hes" module argument, is computationally expensive, one of the (dual) quasi-Newton or conjugate gradient algorithms might be more efficient.

In addition to the standard iteration history, the NLPTR subroutine prints the following information:

Under the heading Iter, an asterisk (*) printed after the iteration number indicates that the computed Hessian approximation was singular and had to be ridged with a positive value.
The heading lambda represents the Lagrange multiplier, 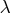$\lambda$ . This has a value of zero when the optimum of the quadratic function approximation is inside the trust region, in which case a trust-region-scaled Newton step is performed. It is greater than zero when the optimum is at the boundary of the trust region, in which case the scaled Newton step is too long to fit in the trust region and a quadratically constrained optimization is done. Large values indicate optimization difficulties, and as in Gay (1983), a negative value indicates the special case of an indefinite Hessian matrix.
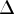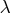The heading radius refers to $\delta$ , the radius of the trust region. Small values of the radius combined with large values of $\lambda$ in subsequent iterations indicate optimization problems.

For an example of the use of the NLPTR subroutine, see the section "Unconstrained Rosenbrock Function".

Top of Page