| Language Reference |
NLPNMS Call
nonlinear optimization by Nelder-Mead simplex method
- CALL NLPNMS( rc, xr, "fun", x0 <,opt, blc, tc, par, "ptit", "nlc">);
See the section "Nonlinear Optimization and Related Subroutines" for a listing of all NLP subroutines. See Chapter 11 for a description of the inputs to and outputs of all NLP subroutines.
The Nelder-Mead simplex method is one of the subroutines that
can solve optimization problems with nonlinear constraints.
It does not use any derivatives, and it does not assume
that the objective function has continuous derivatives.
However, the objective function must be continuous.
The NLPNMS technique uses a large number of function calls,
and it can be unable to generate precise results when 
.
The NLPNMS subroutine uses the following simplex algorithms:
- For unconstrained or only boundary-constrained problems, the original Nelder-Mead simplex algorithm is implemented and extended to boundary constraints. This algorithm does not compute the objective for infeasible points, and it is invoked if the "nlc" module argument is not specified and the blc argument contains at most two rows (corresponding to lower and upper bounds).
- For linearly or nonlinearly constrained problems, a slightly modified version of Powell's (1992) Constrained Optimization BY Linear Approximations (COBYLA) implementation is used. This algorithm is invoked if the "nlc" module argument is specified or if at least one linear constraint is specified with the blc argument.
The original Nelder-Mead algorithm cannot be used for general linear or nonlinear constraints, but in the unconstrained or boundary-constrained cases, it can be faster. It changes the shape of the simplex by adapting the nonlinearities of the objective function; this contributes to an increased speed of convergence.
Powell's COBYLA Algorithm
Powell's COBYLA algorithm is a sequential
trust-region algorithm that tries to maintain a
regularly shaped simplex throughout the iterations.
The algorithm uses a monotone-decreasing
radius, 
, of a spheric trust region.
The modification implemented in the NLPNMS call permits an
increase of the trust-region radius in special situations.
A sequence of iterations is performed with a constant
trust-region radius until the computed function
reduction is much less than the predicted reduction.
Then, the trust-region radius is reduced.
The trust-region radius is increased only if the
computed function reduction is relatively close to the
predicted reduction and if the simplex is well-shaped.
The start radius, 
, can be specified
with the second element of the par argument,
and the final radius, 
, can be specified
with the ninth element of the tc argument.
Convergence to small values of , or high-precision
convergence, can require many calls of the function and
constraint modules and can result in numerical problems.
The main reasons for the slow convergence
of the COBYLA algorithm are as follows:
- Linear approximations of the objective and constraint functions are used locally.
- Maintaining the regularly shaped simplex and not adapting its shape to nonlinearities yields very small simplexes for highly nonlinear functions, such as fourth-order polynomials.
For more information about the special sets of termination criteria used by the NLPNMS algorithms, see the section "Termination Criteria".
In addition to the standard iteration history, the NLPNMS subroutine prints the following information. For unconstrained or boundary-constrained problems, the subroutine also prints
- difcrit, which, in this subroutine, refers
to the difference between the largest and smallest
function values of the
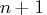simplex vertices
- std, which is the standard deviation of the function values of the simplex vertices
- deltax, which is the vertex length of a restarted simplex. If there are convergence problems, the algorithm restarts the iteration process with a simplex of smaller vertex length.
- size, which is the average
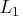distance
of the simplex vertex with the smallest
function value to the other simplex vertices
- conmax is the maximum constraint violation.
- meritf is the value of the merit function,
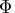. - difmerit is the difference between adjacent values of the merit function.
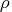- is the trust-region radius.
The following code uses the NLPNMS call to solve the Rosen-Suzuki problem (see the section "Rosen-Suzuki Problem"), which has three nonlinear constraints:
start F_HS43(x);
f = x*x` + x[3]*x[3] - 5*(x[1] + x[2]) - 21*x[3] + 7*x[4];
return(f);
finish F_HS43;
start C_HS43(x);
c = j(3,1,0.);
c[1] = 8 - x*x` - x[1] + x[2] - x[3] + x[4];
c[2] = 10 - x*x` - x[2]*x[2] - x[4]*x[4] + x[1] + x[4];
c[3] = 5 - 2.*x[1]*x[1] - x[2]*x[2] - x[3]*x[3]
- 2.*x[1] + x[2] + x[4];
return(c);
finish C_HS43;
x = j(1,4,1);
optn= j(1,11,.); optn[2]= 3; optn[10]= 3; optn[11]=0;
call nlpnms(rc,xres,"F_HS43",x,optn,,,,,"C_HS43");
Part of the output produced by the preceding code follows.
Optimization Start
Parameter Estimates
N Parameter Estimate
1 X1 1.000000
2 X2 1.000000
3 X3 1.000000
4 X4 1.000000
Value of Objective Function = -19
Values of Nonlinear Constraints
Constraint Residual
[ 1 ] 4.0000
[ 2 ] 6.0000
[ 3 ] 1.0000
Nelder-Mead Simplex Optimization
COBYLA Algorithm by M.J.D. Powell (1992)
Minimum Iterations 0
Maximum Iterations 1000
Maximum Function Calls 3000
Iterations Reducing Constraint Violation 0
ABSFCONV Function Criterion 0
FCONV Function Criterion 2.220446E-16
FCONV2 Function Criterion 1E-6
FSIZE Parameter 0
ABSXCONV Parameter Change Criterion 0.0001
XCONV Parameter Change Criterion 0
XSIZE Parameter 0
ABSCONV Function Criterion -1.34078E154
Initial Simplex Size (INSTEP) 0.5
Singularity Tolerance (SINGULAR) 1E-8
Nelder-Mead Simplex Optimization
COBYLA Algorithm by M.J.D. Powell (1992)
Parameter Estimates 4
Nonlinear Constraints 3
Optimization Start
Objective Function -29.5 Maximum Constraint Violation 4.5
Maximum
Function Objective Constraint
Iter Restarts Calls Function Violation
1 0 12 -52.80342 4.3411
2 0 17 -39.51475 0.0227
3 0 53 -44.02098 0.00949
4 0 62 -44.00214 0.000833
5 0 72 -44.00009 0.000033
6 0 79 -44.00000 1.783E-6
7 0 90 -44.00000 1.363E-7
8 0 94 -44.00000 1.543E-8
Between
Actual
Merit and
Merit Function Predicted
Iter Function Change Change
1 -42.3031 12.803 1.000
2 -39.3797 -2.923 0.250
3 -43.9727 4.593 0.0625
4 -43.9977 0.0249 0.0156
5 -43.9999 0.00226 0.0039
6 -44.0000 0.00007 0.0010
7 -44.0000 1.74E-6 0.0002
8 -44.0000 5.33E-7 0.0001
Optimization Results
Iterations 8 Function Calls 95
Restarts 0 Objective Function -44.00000003
Maximum Constraint Violation 1.543059E-8 Merit Function -43.99999999
Actual Over Pred Change 0.0001
ABSXCONV convergence criterion satisfied.
WARNING: The point x is feasible only at the LCEPSILON= 1E-7 range.
Optimization Results
Parameter Estimates
N Parameter Estimate
1 X1 -0.000034167
2 X2 1.000004
3 X3 2.000023
4 X4 -0.999971
Value of Objective Function = -44.00000003
Values of Nonlinear Constraints
Constraint Residual
[ 1 ] -1.54E-8 *?*
[ 2 ] 1.0000
[ 3 ] -1.5E-8 *?*
Copyright © 2009 by SAS Institute Inc., Cary, NC, USA. All rights reserved.