Language Reference: NLPDD Call :: SAS/IML(R) 9.2 User's Guide

Language Reference

NLPDD Call

nonlinear optimization by double dogleg method

CALL NLPDD( rc, xr, "fun", x0 <,opt, blc, tc, par, "ptit", "grd">);

See the section "Nonlinear Optimization and Related Subroutines" for a listing of all NLP subroutines. See Chapter 11 for a description of the inputs to and outputs of all NLP subroutines.

The double dogleg optimization method combines the ideas of the quasi-Newton and trust-region methods. In each iteration, the algorithm computes the step, $s^{(k)}$ , as a linear combination of the steepest descent or ascent search direction, $s_1^{(k)}$ , and a quasi-Newton search direction, $s_2^{(k)}$ , as follows:

$s^{(k)} = \alpha_1 s_1^{(k)} + \alpha_2 s_2^{(k)}$

The step $s^{(k)}$ must remain within a specified trust-region radius (refer to Fletcher 1987). Hence, the NLPDD subroutine uses the dual quasi-Newton update but does not perform a line search. You can specify one of two update formulas with the fourth element of the opt input argument.

*Value of opt[4]*	Update Method
1	Dual BFGS update of the Cholesky factor of the Hessian matrix.
	This is the default.
2	Dual DFP update of the Cholesky factor of the Hessian matrix

The double dogleg optimization technique works well for medium to moderately large optimization problems, in which the objective function and the gradient are much faster to compute than the Hessian. The implementation is based on Dennis and Mei (1979) and Gay (1983), but it is extended for boundary and linear constraints. The NLPDD subroutine generally needs more iterations than the techniques that require second-order derivatives (NLPTR, NLPNRA, and NLPNRR), but each of the NLPDD iterations is computationally inexpensive. Furthermore, the NLPDD subroutine needs only gradient calls to update the Cholesky factor of an approximate Hessian.

In addition to the standard iteration history, the NLPDD routine prints the following information:

The heading lambda refers to the parameter 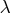$\lambda$ of the double dogleg step. A value of 0 corresponds to the full (quasi-) Newton step.
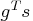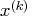The heading slope refers to , the slope of the search direction at the current parameter iterate $x^{(k)}$ . For minimization, this value should be significantly smaller than zero.

The following statements invoke the NLPDD subroutine to solve the constrained Betts optimization problem (see the section "Constrained Betts Function").

  
    start F_BETTS(x); 
       f = .01 * x[1] * x[1] + x[2] * x[2] - 100.; 
       return(f); 
    finish F_BETTS; 
  
    con = {  2. -50.  .   ., 
            50.  50.  .   ., 
            10.  -1. 1. 10.}; 
    x = {-1. -1.}; 
    optn = {0 1}; 
    call nlpdd(rc,xres,"F_BETTS",x,optn,con);

The preceding statements produce the following iteration history.

  
                         Double Dogleg Optimization 
  
         Dual Broyden - Fletcher - Goldfarb - Shanno Update (DBFGS) 
  
                         Without Parameter Scaling 
                  Gradient Computed by Finite Differences 
  
                    Parameter Estimates               2 
                    Lower Bounds                      2 
                    Upper Bounds                      2 
                    Linear Constraints                1 
  
                          Optimization Start 
  
 Active Constraints            0  Objective Function     -98.5376 
 Max Abs Gradient Element      2  Radius                        1 
  
  
                     Function        Active       Objective 
  Iter    Restarts      Calls   Constraints        Function 
  
     1           0          2             0       -99.54678 
     2           0          3             0       -99.59120 
     3           0          5             0       -99.90252 
     4           0          6             1       -99.96000 
     5           0          7             1       -99.96000 
     6           0          8             1       -99.96000 
  
  
               Objective    Max Abs              Slope of 
                Function   Gradient                Search 
   Iter           Change    Element    Lambda   Direction 
  
      1           1.0092     0.1346     6.012      -1.805 
      2           0.0444     0.1279         0     -0.0228 
      3           0.3113     0.0624         0      -0.209 
      4           0.0575    0.00432         0     -0.0975 
      5          4.66E-6   0.000079         0     -458E-8 
      6         1.559E-9          0         0     -16E-10 
  
  
  
  
                            Optimization Results 
  
 Iterations                              6  Function Calls                9 
 Gradient Calls                          8  Active Constraints            1 
 Objective Function                 -99.96  Max Abs Gradient Element      0 
 Slope of Search Direction     -1.56621E-9  Radius                        1 
  
  
    GCONV convergence criterion satisfied.

Top of Page