| Language Reference |
NLPFDD Call
approximates derivatives by finite-differences method
- CALL NLPFDD( f, g, h, "fun", x0, <,par, "grd">);
See the section "Nonlinear Optimization and Related Subroutines" for a listing of all NLP subroutines. See Chapter 11 for a description of the inputs to and outputs of all NLP subroutines.
The NLPFDD subroutine can be used for the following tasks:
- If the module "fun" returns a scalar, the NLPFDD subroutine computes the function value f, the gradient vector g, and the Hessian matrix h, all evaluated at the point x0.
- If the module "fun" returns a column vector of
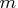 function values, the subroutine assumes that a least squares
function is specified, and it computes the function vector
f, the Jacobian matrix J, and the crossproduct
of the Jacobian matrix
function values, the subroutine assumes that a least squares
function is specified, and it computes the function vector
f, the Jacobian matrix J, and the crossproduct
of the Jacobian matrix 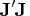 at the point x0.
Note that in this case, you must set the first
element of the par argument to
at the point x0.
Note that in this case, you must set the first
element of the par argument to 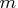 .
.
You can specify the following input arguments with the NLPFDD subroutine:
- The "fun" argument refers to an IML module that returns
either a scalar value or a column vector of length
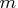 .
This module returns the value of the objective
function or, for least squares problems, the values of
the
.
This module returns the value of the objective
function or, for least squares problems, the values of
the 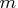 functions that the objective function comprises.
functions that the objective function comprises.
- The x0 argument is a vector of length
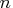 that defines the point at which the
functions and derivatives should be computed.
that defines the point at which the
functions and derivatives should be computed.
- The par argument is a vector that defines options and control parameters. Note that the par argument in the NLPFDD call is different from the one used in the optimization subroutines.
- The "grd" argument is optional and refers to an IML module that returns a vector defining the gradient of the function at x0. If the fun argument returns a vector of values instead of a scalar, the "grd" argument is ignored.
If the "fun" module returns a scalar, the subroutine returns the following values:
- f is the value of the function at the point x0.
- g is a vector containing the value of the gradient at the point x0. If you specify the "grd" argument, the gradient is computed from that module. Otherwise, the approximate gradient is computed by a finite difference approximation using calls of the function module in a neighborhood of x0.
- h is a matrix containing a finite difference approximation of the value of the Hessian at the point x0. If you specify the "grd" argument, the Hessian is computed by calls of that module in a neighborhood of x0. Otherwise, it is computed by calls of the function module in a neighborhood of x0.
- f is a vector containing the values
of the
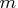 functions comprising the
objective function at the point x0.
functions comprising the
objective function at the point x0.
- g is the
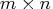 Jacobian matrix J, which
contains the first-order derivatives of the functions
with respect to the parameters, evaluated at x0.
It is computed by finite difference
approximations in a neighborhood of x0.
Jacobian matrix J, which
contains the first-order derivatives of the functions
with respect to the parameters, evaluated at x0.
It is computed by finite difference
approximations in a neighborhood of x0.
- h is the
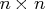 crossproduct of
the Jacobian matrix,
crossproduct of
the Jacobian matrix, 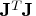 .
It is computed by finite difference
approximations in a neighborhood of x0.
.
It is computed by finite difference
approximations in a neighborhood of x0.
- par[1] corresponds to the opt[1] argument in the optimization subroutines. This argument is relevant only to least squares optimization methods, in which case it specifies the number of functions returned by the module "fun". If par[1] is missing or is smaller than 1, it is set to 1.
- par[2] corresponds to the opt[8]
argument in the optimization subroutines.
It determines what type of approximation is to be used and
how the finite difference interval,
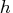 , is to be computed.
See the section "Finite-Difference Approximations of Derivatives" for details.
, is to be computed.
See the section "Finite-Difference Approximations of Derivatives" for details.
- par[3] corresponds to the par[8]
argument in the optimization subroutines.
It specifies the number of accurate digits
in evaluating the objective function.
The default is
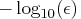 ,
where
,
where 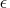 is the machine precision.
is the machine precision.
The NLPFDD subroutine is particularly useful for checking your analytical derivative specifications of the "grd", "hes", and "jac" modules. You can compare the results of the modules with the finite difference approximations of the derivatives of f at the point x0 to verify your specifications.
In the unconstrained Rosenbrock problem (see the section "Unconstrained Rosenbrock Function"), the objective function is
start F_ROSEN(x);
y1 = 10. * (x[2] - x[1] * x[1]);
y2 = 1. - x[1];
f = .5 * (y1 * y1 + y2 * y2);
return(f);
finish F_ROSEN;
x = {2 7};
CALL NLPFDD(crit,grad,hess,"F_ROSEN",x);
print grad;
print hess;
Here is the resulting output:
GRAD
-1199 300.00001
HESS
1000.9998 -400.0018
-400.0018 99.999993
If the Rosenbrock problem is considered from a least squares perspective, the two functions are
start F_ROSEN(x);
y = j(2,1,0.);
y[1] = 10. * (x[2] - x[1] * x[1]);
y[2] = 1. - x[1];
return(y);
finish F_ROSEN;
x = {2 7};
parms = 2;
CALL NLPFDD(fun,jac,crpj,"F_ROSEN",x,parms);
print jac;
print crpj;
The finite difference approximations for the Jacobian follow.
JAC
-40 10
-1 0
CRPJ
1601 -400
-400 100
Copyright © 2009 by SAS Institute Inc., Cary, NC, USA. All rights reserved.
![g^' & = & [ \frac{\partial f}{\partial x_1} \ \frac{\partial f}{\partial x_2}... ...200x_2 + 1 & -200x_1 \ -200x_1 & 100 ] = [ 1001 & -400 \ -400 & 100 ]](images/langref_langrefeq790.gif)
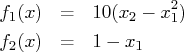
![j & = & [ \frac{\partial f_1}{\partial x_1} & \frac{\partial f_1}{\partial x_2... ...400x_1^2+1 & -200x_1 \ -200x_1 & 100 ] = [ 1601 & -400 \ -400 & 100 ]](images/langref_langrefeq792.gif)