Language Reference

NLPFEA Call

computes feasible points subject to constraints

CALL NLPFEA( xr, x0, blc <,par>);

See the section "Nonlinear Optimization and Related Subroutines" for a listing of all NLP subroutines. See Chapter 11 for a description of the inputs to and outputs of all NLP subroutines.

The NLPFEA subroutine tries to compute a point that is feasible subject to a set of boundary and linear constraints. You can specify boundary and linear constraints that define an empty feasible region, in which case the subroutine returns missing values.

You can specify the following input arguments with the NLPFEA subroutine:

• x0 is a row vector defining the coordinates of a point that is not necessarily feasible for a set of linear and boundary constraints.
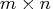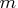• blc is an matrix defining a set of boundary and linear constraints. See the section "Parameter Constraints" for details.
• par is a vector of length two. The argument is different from the one used in the optimization subroutines. The first element sets the LCEPS parameter, which controls how precisely the returned point must satisfy the constraints. The second element sets the LCSING parameter, which specifies the criterion for deciding when constraints are considered linearly dependent. For details, see the section "Control Parameters Vector".

The NLPFEA subroutine returns the xr argument. The result is a vector containing either the coordinates of a feasible point, which indicates that the subroutine was successful, or missing values, which indicates that the subroutine could not find a feasible point.

The following statements call the NLPFEA subroutine with the constraints from the Betts problem (see the section "Constrained Betts Function") and an initial infeasible point . The subroutine returns the feasible point as the vector XFEAS.

  
    con = {  2. -50.  .   ., 
            50.  50.  .   ., 
            10.  -1. 1. 10.}; 
    x = {-17. -61}; 
    call nlpfea(xfeas,x,con);