The SURVEYLOGISTIC Procedure

ESTIMATE Statement

ESTIMATE <'label'> estimate-specification <(divisor=n)><, …<'label'> estimate-specification <(divisor=n)>></ options>;

The ESTIMATE statement provides a mechanism for obtaining custom hypothesis tests. Estimates are formed as linear estimable functions of the form 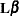$\bL \bbeta$ . You can perform hypothesis tests for the estimable functions, construct confidence limits, and obtain specific nonlinear transformations.

Table 111.4 summarizes the options available in the ESTIMATE statement.

Table 111.4: ESTIMATE Statement Options

Option	Description
Construction and Computation of Estimable Functions
DIVISOR=	Specifies a list of values to divide the coefficients
NOFILL	Suppresses the automatic fill-in of coefficients for higher-order effects
SINGULAR=	Tunes the estimability checking difference
Degrees of Freedom and p-values
ADJUST=	Determines the method for multiple comparison adjustment of estimates
ALPHA= $\alpha$	Determines the confidence level ( $1-\alpha$ )
LOWER	Performs one-sided, lower-tailed inference
STEPDOWN	Adjusts multiplicity-corrected p-values further in a step-down fashion
TESTVALUE=	Specifies values under the null hypothesis for tests
UPPER	Performs one-sided, upper-tailed inference
Statistical Output
CL	Constructs confidence limits
CORR	Displays the correlation matrix of estimates
COV	Displays the covariance matrix of estimates
E	Prints the $\mb{L}$ matrix
JOINT	Produces a joint F or chi-square test for the estimable functions
PLOTS=	Requests ODS statistical graphics if the analysis is sampling-based
SEED=	Specifies the seed for computations that depend on random numbers
Generalized Linear Modeling
CATEGORY=	Specifies how to construct estimable functions with multinomial data
EXP	Exponentiates and displays estimates
ILINK	Computes and displays estimates and standard errors on the inverse linked scale

For details about the syntax of the ESTIMATE statement, see the section ESTIMATE Statement in Chapter 19: Shared Concepts and Topics.