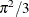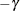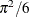The SURVEYLOGISTIC Procedure

Model Specification

Subsections:

Response Level Ordering

Response level ordering is important because, by default, PROC SURVEYLOGISTIC models the probabilities of response levels with lower Ordered Values. Ordered Values, displayed in the "Response Profile" table, are assigned to response levels in ascending sorted order. That is, the lowest response level is assigned Ordered Value 1, the next lowest is assigned Ordered Value 2, and so on. For example, if your response variable Y takes values in 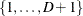$\{ 1,\ldots ,D+1\} $, then the functions of the response probabilities modeled with the cumulative model are

\[ \mbox{logit}(\Pr (Y\le i | \mb{x})), i=1,\ldots ,D \]

and for the generalized logit model they are

\[ \log \left(\frac{\Pr (Y=i | \mb{x})}{\Pr (Y=D+1 | \mb{x})}\right), i=1,\ldots ,D \]

where the highest Ordered Value 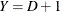$Y=D+1$ is the reference level. You can change these default functions by specifying the EVENT= , REF= , DESCENDING , or ORDER= response variable options in the MODEL statement.

For binary response data with event and nonevent categories, the procedure models the function

\[ \mbox{logit}(p) = \log \left(\frac{p}{1-p}\right) \]

where p is the probability of the response level assigned to Ordered Value 1 in the "Response Profiles" table. Since

\[ \mbox{logit}(p) = -\mbox{logit}(1-p) \]

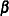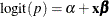the effect of reversing the order of the two response levels is to change the signs of $\alpha $ and $\bbeta $ in the model $\mbox{logit}(p) = \alpha + \mb{x}\bbeta $.

If your event category has a higher Ordered Value than the nonevent category, the procedure models the nonevent probability. You can use response variable options to model the event probability. For example, suppose the binary response variable Y takes the values 1 and 0 for event and nonevent, respectively, and Exposure is the explanatory variable. By default, the procedure assigns Ordered Value 1 to response level Y=0, and Ordered Value 2 to response level Y=1. Therefore, the procedure models the probability of the nonevent (Ordered Value=1) category. To model the event probability, you can do the following:

  • Explicitly state which response level is to be modeled by using the response variable option EVENT= in the MODEL statement: 

    model Y(event='1') = Exposure;

  • Specify the response variable option DESCENDING in the MODEL statement: 

    model Y(descending)=Exposure;

  • Specify the response variable option REF= in the MODEL statement as the nonevent category for the response variable. This option is most useful when you are fitting a generalized logit model. 

    model Y(ref='0') = Exposure;

  • Assign a format to Y such that the first formatted value (when the formatted values are put in sorted order) corresponds to the event. For this example, Y=1 is assigned formatted value 'event' and Y=0 is assigned formatted value 'nonevent.' Since ORDER= FORMATTED by default, Ordered Value 1 is assigned to response level Y=1 so the procedure models the event. 

    proc format;
   value Disease 1='event' 0='nonevent';
run;

proc surveylogistic;
   format Y Disease.;
   model Y=Exposure;
run;

CLASS Variable Parameterization

Consider a model with one CLASS variable A with four levels: 1, 2, 5, and 7. Details of the possible choices for the PARAM= option follow.

EFFECT

Three columns are created to indicate group membership of the nonreference levels. For the reference level, all three dummy variables have a value of –1. For instance, if the reference level is 7 (REF=7), the design matrix columns for A are as follows.

 

Design Matrix

A

A1

A2

A5

1

1

0

0

2

0

1

0

5

0

0

1

7

–1

–1

–1

For CLASS main effects that use the EFFECT coding scheme, individual parameters correspond to the difference between the effect of each nonreference level and the average over all four levels.

GLM

As in PROC GLM, four columns are created to indicate group membership. The design matrix columns for A are as follows.

 

Design Matrix

A

A1

A2

A5

A7

1

1

0

0

0

2

0

1

0

0

5

0

0

1

0

7

0

0

0

1

For CLASS main effects that use the GLM coding scheme, individual parameters correspond to the difference between the effect of each level and the last level.

ORDINAL

Three columns are created to indicate group membership of the higher levels of the effect. For the first level of the effect (which for A is 1), all three dummy variables have a value of 0. The design matrix columns for A are as follows.

 

Design Matrix

A

A2

A5

A7

1

0

0

0

2

1

0

0

5

1

1

0

7

1

1

1

The first level of the effect is a control or baseline level.

For CLASS main effects that use the ORDINAL coding scheme, the first level of the effect is a control or baseline level; individual parameters correspond to the difference between effects of the current level and the preceding level. When the parameters for an ordinal main effect have the same sign, the response effect is monotonic across the levels.

POLYNOMIAL | POLY

Three columns are created. The first represents the linear term (x), the second represents the quadratic term (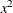$x^2$), and the third represents the cubic term (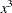$x^3$), where x is the level value. If the CLASS levels are not numeric, they are translated into 1, 2, 3, $\dots $ according to their sort order. The design matrix columns for A are as follows.

 

Design Matrix

A

APOLY1

APOLY2

APOLY3

1

1

1

1

2

2

4

8

5

5

25

125

7

7

49

343

REFERENCE | REF

Three columns are created to indicate group membership of the nonreference levels. For the reference level, all three dummy variables have a value of 0. For instance, if the reference level is 7 (REF=7), the design matrix columns for A are as follows.

 

Design Matrix

A

A1

A2

A5

1

1

0

0

2

0

1

0

5

0

0

1

7

0

0

0

For CLASS main effects that use the REFERENCE coding scheme, individual parameters correspond to the difference between the effect of each nonreference level and the reference level.

ORTHEFFECT

The columns are obtained by applying the Gram-Schmidt orthogonalization to the columns for PARAM=EFFECT. The design matrix columns for A are as follows.

 

Design Matrix

A

AOEFF1

AOEFF2

AOEFF3

1

1.41421

–0.81650

–0.57735

2

0.00000

1.63299

–0.57735

5

0.00000

0.00000

1.73205

7

–1.41421

–0.81649

–0.57735

ORTHORDINAL | ORTHOTHERM

The columns are obtained by applying the Gram-Schmidt orthogonalization to the columns for PARAM=ORDINAL. The design matrix columns for A are as follows.

 

Design Matrix

A

AOORD1

AOORD2

AOORD3

1

–1.73205

0.00000

0.00000

2

0.57735

–1.63299

0.00000

5

0.57735

0.81650

–1.41421

7

0.57735

0.81650

1.41421

ORTHPOLY

The columns are obtained by applying the Gram-Schmidt orthogonalization to the columns for PARAM=POLY. The design matrix columns for A are as follows.

 

Design Matrix

A

AOPOLY1

AOPOLY2

AOPOLY5

1

–1.153

0.907

–0.921

2

–0.734

–0.540

1.473

5

0.524

–1.370

–0.921

7

1.363

1.004

0.368

ORTHREF

The columns are obtained by applying the Gram-Schmidt orthogonalization to the columns for PARAM=REFERENCE. The design matrix columns for A are as follows.

 

Design Matrix

A

AOREF1

AOREF2

AOREF3

1

1.73205

0.00000

0.00000

2

–0.57735

1.63299

0.00000

5

–0.57735

–0.81650

1.41421

7

–0.57735

–0.81650

–1.41421

Link Functions and the Corresponding Distributions

Four link functions are available in the SURVEYLOGISTIC procedure. The logit function is the default. To specify a different link function, use the LINK= option in the MODEL statement. The link functions and the corresponding distributions are as follows:

  • The logit function

    \[ g(p)=\log \left( \frac{p}{1-p} \right) \]

    is the inverse of the cumulative logistic distribution function, which is

    \[ F(x)=\frac{1}{1+e^{-x}} \]

  • The probit (or normit) function

    \[ g(p)=\Phi ^{-1}(p) \]

    is the inverse of the cumulative standard normal distribution function, which is

    \[ F(x)=\Phi (x)=\frac{1}{\sqrt {2\pi }}\int _{-\infty }^ x e^{-\frac{1}{2} z^2} dz \]

    Traditionally, the probit function includes an additive constant 5, but throughout PROC SURVEYLOGISTIC, the terms probit and normit are used interchangeably, previously defined as $g(p)$.

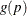  • The complementary log-log function

    \[ g(p)=\log (-\log (1-p)) \]

    is the inverse of the cumulative extreme-value function (also called the Gompertz distribution), which is

    \[ F(x)=1-e^{-e^ x} \]

  • The generalized logit function extends the binary logit link to a vector of levels 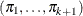$(\pi _1,\ldots ,\pi _{k+1})$ by contrasting each level with a fixed level

    \[ g(\pi _ i)=\log \left( \frac{\pi _ i}{\pi _{k+1}} \right) \quad i=1,\ldots , k \]

The variances of the normal, logistic, and extreme-value distributions are not the same. Their respective means and variances are

Distribution

Mean

Variance

Normal

0

1

Logistic

0

$\pi ^2/3$

Extreme-value

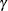$-\gamma $

$\pi ^2/6$

where $\gamma $ is the Euler constant. In comparing parameter estimates that use different link functions, you need to take into account the different scalings of the corresponding distributions and, for the complementary log-log function, a possible shift in location. 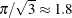For example, if the fitted probabilities are in the neighborhood of 0.1 to 0.9, then the parameter estimates from using the logit link function should be about $\pi /\sqrt {3}\approx 1.8$ larger than the estimates from the probit link function.