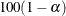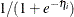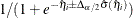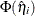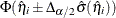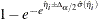The SURVEYLOGISTIC Procedure
- Overview
- Getting Started
-
Syntax
 PROC SURVEYLOGISTIC StatementBY StatementCLASS StatementCLUSTER StatementCONTRAST StatementDOMAIN StatementEFFECT StatementESTIMATE StatementFREQ StatementLSMEANS StatementLSMESTIMATE StatementMODEL StatementOUTPUT StatementREPWEIGHTS StatementSLICE StatementSTORE StatementSTRATA StatementTEST StatementUNITS StatementWEIGHT Statement
PROC SURVEYLOGISTIC StatementBY StatementCLASS StatementCLUSTER StatementCONTRAST StatementDOMAIN StatementEFFECT StatementESTIMATE StatementFREQ StatementLSMEANS StatementLSMESTIMATE StatementMODEL StatementOUTPUT StatementREPWEIGHTS StatementSLICE StatementSTORE StatementSTRATA StatementTEST StatementUNITS StatementWEIGHT Statement -
Details
 Missing ValuesModel SpecificationModel FittingSurvey Design InformationLogistic Regression Models and ParametersVariance EstimationDomain AnalysisHypothesis Testing and EstimationLinear Predictor, Predicted Probability, and Confidence LimitsOutput Data SetsDisplayed OutputODS Table NamesODS Graphics
Missing ValuesModel SpecificationModel FittingSurvey Design InformationLogistic Regression Models and ParametersVariance EstimationDomain AnalysisHypothesis Testing and EstimationLinear Predictor, Predicted Probability, and Confidence LimitsOutput Data SetsDisplayed OutputODS Table NamesODS Graphics -
Examples

- References
Linear Predictor, Predicted Probability, and Confidence Limits
This section describes how predicted probabilities and confidence limits are calculated by using the pseudo-estimates (MLEs) obtained from PROC SURVEYLOGISTIC. For a specific example, see the section Getting Started: SURVEYLOGISTIC Procedure. Predicted probabilities and confidence limits can be output to a data set with the OUTPUT statement.
Let  is the
is the 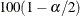 th percentile point of a standard normal distribution or a t distribution according to the DF=
specification:
th percentile point of a standard normal distribution or a t distribution according to the DF=
specification:

Cumulative Response Models
For a row vector of explanatory variables  , the linear predictor
, the linear predictor
![\[ \eta _ i= g(\mbox{Pr}(Y\leq i~ |~ \mb{x})) = \alpha _ i+\mb{x}\bbeta , \quad 1 \leq i \leq k \]](images/statug_surveylogistic0371.png)
is estimated by
![\[ \hat{\eta }_ i=\hat{\alpha }_ i+\mb{x}\hat{\bbeta } \]](images/statug_surveylogistic0372.png)
where 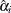 and
and 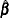 are the MLEs of
are the MLEs of 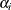 and
and 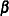 . The estimated standard error of
. The estimated standard error of 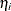 is
is 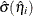 , which can be computed as the square root of the quadratic form
, which can be computed as the square root of the quadratic form 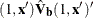 , where
, where 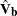 is the estimated covariance matrix of the parameter estimates. The asymptotic
is the estimated covariance matrix of the parameter estimates. The asymptotic 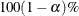 confidence interval for
confidence interval for 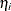 is given by
is given by
![\[ \hat{\eta }_ i\pm \Delta _{\alpha /2}\hat{\sigma }({\hat{\eta }}_ i) \]](images/statug_surveylogistic0381.png)
The predicted value and the 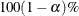 confidence limits for Pr
confidence limits for Pr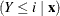 are obtained by back-transforming the corresponding measures for the linear predictor.
are obtained by back-transforming the corresponding measures for the linear predictor.
|
Link |
Predicted Probability |
|
|---|---|---|
|
LOGIT |
|
|
|
PROBIT |
|
|
|
CLOGLOG |
|
|
Generalized Logit Model
For a vector of explanatory variables  , let
, let 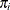 denote the probability of obtaining the response value i:
denote the probability of obtaining the response value i:
![\[ \pi _ i = \left\{ \begin{array}{ll} \pi _{k+1} {e}^{\alpha _ i+\mb{x}\bbeta _ i} & 1\le i\le k \\ \displaystyle \frac{1}{1+\sum _{j=1}^{k} {e}^{\alpha _ j+\mb{x} {\bbeta }_ j}} & i=k+1 \end{array} \right. \]](images/statug_surveylogistic0390.png)
By the delta method,
![\[ \sigma ^2({\pi }_ i) = \biggl ( \frac{\partial \pi _ i}{\partial \btheta } \biggr )’ \bV ({\btheta }) \frac{\partial \pi _ i}{\partial \btheta } \]](images/statug_surveylogistic0391.png)
A 100(1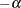 )% confidence level for
)% confidence level for 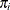 is given by
is given by
![\[ \hat{\pi }_ i \pm \Delta _{\alpha /2} \hat{\sigma }(\hat{\pi }_ i) \]](images/statug_surveylogistic0393.png)
where 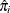 is the estimated expected probability of response i and
is the estimated expected probability of response i and 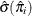 is obtained by evaluating
is obtained by evaluating 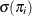 at
at 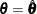 .
.