The SURVEYLOGISTIC Procedure
- Overview
- Getting Started
-
Syntax
 PROC SURVEYLOGISTIC StatementBY StatementCLASS StatementCLUSTER StatementCONTRAST StatementDOMAIN StatementEFFECT StatementESTIMATE StatementFREQ StatementLSMEANS StatementLSMESTIMATE StatementMODEL StatementOUTPUT StatementREPWEIGHTS StatementSLICE StatementSTORE StatementSTRATA StatementTEST StatementUNITS StatementWEIGHT Statement
PROC SURVEYLOGISTIC StatementBY StatementCLASS StatementCLUSTER StatementCONTRAST StatementDOMAIN StatementEFFECT StatementESTIMATE StatementFREQ StatementLSMEANS StatementLSMESTIMATE StatementMODEL StatementOUTPUT StatementREPWEIGHTS StatementSLICE StatementSTORE StatementSTRATA StatementTEST StatementUNITS StatementWEIGHT Statement -
Details
 Missing ValuesModel SpecificationModel FittingSurvey Design InformationLogistic Regression Models and ParametersVariance EstimationDomain AnalysisHypothesis Testing and EstimationLinear Predictor, Predicted Probability, and Confidence LimitsOutput Data SetsDisplayed OutputODS Table NamesODS Graphics
Missing ValuesModel SpecificationModel FittingSurvey Design InformationLogistic Regression Models and ParametersVariance EstimationDomain AnalysisHypothesis Testing and EstimationLinear Predictor, Predicted Probability, and Confidence LimitsOutput Data SetsDisplayed OutputODS Table NamesODS Graphics -
Examples

- References
MODEL Statement
-
MODEL events/trials = <effects </ options>>;
-
MODEL variable <(v-options)> = <effects> </ options>;
The MODEL statement names the response variable and the explanatory effects, including covariates, main effects, interactions, and nested effects; see the section Specification of Effects in Chapter 46: The GLM Procedure, for more information. If you omit the explanatory variables, the procedure fits an intercept-only model. Model options can be specified after a slash (/).
Two forms of the MODEL statement can be specified. The first form, referred to as single-trial syntax, is applicable to binary, ordinal, and nominal response data. The second form, referred to as events/trials syntax, is restricted to the case of binary response data. The single-trial syntax is used when each observation in the DATA= data set contains information about only a single trial, such as a single subject in an experiment. When each observation contains information about multiple binary-response trials, such as the counts of the number of subjects observed and the number responding, then events/trials syntax can be used.
In the events/trials syntax, you specify two variables that contain count data for a binomial experiment. These two variables are separated by a slash. The value of the first variable, events, is the number of positive responses (or events), and it must be nonnegative. The value of the second variable, trials, is the number of trials, and it must not be less than the value of events.
In the single-trial syntax, you specify one variable (on the left side of the equal sign) as the response variable. This variable can be character or numeric. Options specific to the response variable can be specified immediately after the response variable with parentheses around them.
For both forms of the MODEL statement, explanatory effects follow the equal sign. Variables can be either continuous or classification variables. Classification variables can be character or numeric, and they must be declared in the CLASS statement. When an effect is a classification variable, the procedure enters a set of coded columns into the design matrix instead of directly entering a single column containing the values of the variable.
Response Variable Options
You specify the following options by enclosing them in parentheses after the response variable:
Model Options
Model options can be specified after a slash (/). Table 111.7 summarizes the options available in the MODEL statement.
Table 111.7: MODEL Statement Options
|
Option |
Description |
|---|---|
|
Model Specification Options |
|
|
Specifies link function |
|
|
Suppresses intercept(s) |
|
|
Specifies offset variable |
|
|
Convergence Criterion Options |
|
|
Specifies absolute function convergence criterion |
|
|
Specifies relative function convergence criterion |
|
|
Specifies relative gradient convergence criterion |
|
|
Specifies relative parameter convergence criterion |
|
|
Specifies maximum number of iterations |
|
|
Suppresses checking for infinite parameters |
|
|
Specifies technique used to improve the log-likelihood function when its value is worse than that of the previous step |
|
|
Specifies tolerance for testing singularity |
|
|
Specifies iterative algorithm for maximization |
|
|
Options for Adjustment to Variance Estimation |
|
|
Chooses variance estimation adjustment method |
|
|
Options for Confidence Intervals |
|
|
Specifies the degrees of freedom |
|
|
Specifies |
|
|
Specifies the type of likelihood ratio chi-square test |
|
|
Computes confidence intervals for parameters |
|
|
Computes confidence intervals for odds ratios |
|
|
Options for Display of Details |
|
|
Displays correlation matrix |
|
|
Displays covariance matrix |
|
|
Displays exponentiated values of estimates |
|
|
Displays gradients evaluated at null hypothesis |
|
|
Displays iteration history |
|
|
Suppresses "Class Level Information" table |
|
|
Displays parameter labels |
|
|
Displays generalized |
|
|
Displays standardized estimates |
|
The following list describes these options:

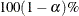
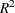
![\[ |l^{(i)} - l^{(i-1)}| < \mi{value} \]](images/statug_surveylogistic0055.png)

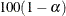


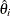
![\[ \frac{ |l^{(i)} - l^{(i-1)}|}{|l^{(i-1)}| + {\mbox{1E--6}}} < \mi{value} \]](images/statug_surveylogistic0061.png)
![\[ \frac{{\mb{g}^{(i)}}^{\prime } \mb{I}^{(i)} \mb{g}^{(i)}}{|l^{(i)}| + {\mbox{1E--6}}} < \mi{value} \]](images/statug_surveylogistic0062.png)


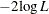









![\[ \max _ j |\delta _ j^{(i)}| < \mi{value} \]](images/statug_surveylogistic0074.png)