The QLIM Procedure
- Overview
-
Getting Started

-
Syntax

-
Details
 Ordinal Discrete Choice ModelingLimited Dependent Variable ModelsStochastic Frontier Production and Cost ModelsHeteroscedasticity and Box-Cox TransformationBivariate Limited Dependent Variable ModelingSelection ModelsMultivariate Limited Dependent ModelsVariable SelectionTests on ParametersEndogeneity and Instrumental VariablesPanel Data AnalysisBayesian AnalysisPrior DistributionsAutomated MCMCMarginal LikelihoodStandard DistributionsOutput to SAS Data SetOUTEST= Data SetNamingODS Table NamesODS Graphics
Ordinal Discrete Choice ModelingLimited Dependent Variable ModelsStochastic Frontier Production and Cost ModelsHeteroscedasticity and Box-Cox TransformationBivariate Limited Dependent Variable ModelingSelection ModelsMultivariate Limited Dependent ModelsVariable SelectionTests on ParametersEndogeneity and Instrumental VariablesPanel Data AnalysisBayesian AnalysisPrior DistributionsAutomated MCMCMarginal LikelihoodStandard DistributionsOutput to SAS Data SetOUTEST= Data SetNamingODS Table NamesODS Graphics -
Examples

- References
Standard Distributions
Table 29.3 through Table 29.10 show all the distribution density functions that PROC QLIM recognizes. You specify these distribution densities in the PRIOR statement.
Table 29.3: Beta Distribution
|
PRIOR statement |
BETA(SHAPE1=a, SHAPE2=b, MIN=m, MAX=M) |
|
Note: Commonly |
|
|
Density |
|
|
Parameter restriction |
|
|
Range |
|
|
Mean |
|
|
Variance |
|
|
Mode |
|
|
Defaults |
SHAPE1=SHAPE2=1, |
Table 29.4: Gamma Distribution
|
PRIOR statement |
GAMMA(SHAPE=a, SCALE=b ) |
|
Density |
|
|
Parameter restriction |
|
|
Range |
|
|
Mean |
|
|
Variance |
|
|
Mode |
|
|
Defaults |
SHAPE=SCALE=1 |
Table 29.5: Square Root Gamma Distribution
|
PRIOR statement |
SQGAMMA(SHAPE=a, SCALE=b ) |
|
Density |
|
|
Parameter restriction |
|
|
Range |
|
|
Mean |
|
|
Variance |
|
|
Mode |
|
|
Defaults |
SHAPE=SCALE=1 |
|
See Stacy (1962) for more details. |
Table 29.6: Inverse-Gamma Distribution
|
PRIOR statement |
IGAMMA(SHAPE=a, SCALE=b) |
|
Density |
|
|
Parameter restriction |
|
|
Range |
|
|
Mean |
|
|
Variance |
|
|
Mode |
|
|
Defaults |
SHAPE=2.000001, SCALE=1 |
Table 29.7: Square Root Inverse-Gamma Distribution
|
PRIOR statement |
SQIGAMMA(SHAPE=a, SCALE=b) |
|
Density |
|
|
Parameter restriction |
|
|
Range |
|
|
Mean |
|
|
Variance |
|
|
Mode |
|
|
Defaults |
SHAPE=2.000001, SCALE=1 |
|
See Stacy (1962) for more details. |
Table 29.8: Normal Distribution
|
PRIOR statement |
NORMAL(MEAN= |
|
Density |
|
|
Parameter restriction |
|
|
Range |
|
|
Mean |
|
|
Variance |
|
|
Mode |
|
|
Defaults |
MEAN=0, VAR=1000000 |
Table 29.9: t Distribution
|
PRIOR statement |
T(LOCATION= |
|
Density |
|
|
Parameter restriction |
|
|
Range |
|
|
Mean |
|
|
Variance |
|
|
Mode |
|
|
Defaults |
LOCATION=0, DF=3 |
Table 29.10: Uniform Distribution
|
PRIOR statement |
UNIFORM(MIN=m, MAX=M) |
|
Density |
|
|
Parameter restriction |
|
|
Range |
|
|
Mean |
|
|
Variance |
|
|
Mode |
Not unique |
|
Defaults |
MIN |






![$ \left\{ \begin{array}{ll} \left[ m, M \right] & \mbox{when } a = 1, b = 1 \\ \left[ m, M \right) & \mbox{when } a = 1, b \neq 1 \\ \left( m, M \right] & \mbox{when } a \neq 1, b = 1 \\ \left( m, M \right) & \mbox{otherwise} \end{array} \right. $](images/etsug_qlim0479.png)













![$\left\{ a-\left[\frac{\Gamma (a+\frac{1}{2})}{\Gamma (a)}\right]^{2}\right\} b$](images/etsug_qlim0493.png)









![$\left\{ \frac{1}{a-1}-\left[\frac{\Gamma (a-\frac{1}{2})}{\Gamma (a)}\right]^{2}\right\} b,\qquad a>1$](images/etsug_qlim0503.png)

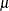
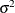




![$\frac{\Gamma \left(\frac{\nu +1}{2}\right)}{\Gamma \left(\frac{\nu }{2}\right)\sqrt {\pi \nu }}\left[1+\frac{(\theta -\mu )^2}{\nu }\right]^{-\frac{\nu +1}{2}} $](images/etsug_qlim0508.png)




![$ \theta \in [m, M]$](images/etsug_qlim0513.png)



