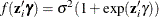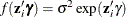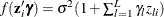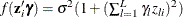The QLIM Procedure
- Overview
-
Getting Started

-
Syntax

-
Details
 Ordinal Discrete Choice ModelingLimited Dependent Variable ModelsStochastic Frontier Production and Cost ModelsHeteroscedasticity and Box-Cox TransformationBivariate Limited Dependent Variable ModelingSelection ModelsMultivariate Limited Dependent ModelsVariable SelectionTests on ParametersEndogeneity and Instrumental VariablesPanel Data AnalysisBayesian AnalysisPrior DistributionsAutomated MCMCMarginal LikelihoodStandard DistributionsOutput to SAS Data SetOUTEST= Data SetNamingODS Table NamesODS Graphics
Ordinal Discrete Choice ModelingLimited Dependent Variable ModelsStochastic Frontier Production and Cost ModelsHeteroscedasticity and Box-Cox TransformationBivariate Limited Dependent Variable ModelingSelection ModelsMultivariate Limited Dependent ModelsVariable SelectionTests on ParametersEndogeneity and Instrumental VariablesPanel Data AnalysisBayesian AnalysisPrior DistributionsAutomated MCMCMarginal LikelihoodStandard DistributionsOutput to SAS Data SetOUTEST= Data SetNamingODS Table NamesODS Graphics -
Examples

- References
Heteroscedasticity and Box-Cox Transformation
Heteroscedasticity
If the variance of regression disturbance, (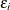 ), is heteroscedastic, the variance can be specified as a function of variables
), is heteroscedastic, the variance can be specified as a function of variables
![\[ E(\epsilon _{i}^{2}) = \sigma _{i}^{2} = f(\mb{z}_{i}’\bgamma ) \]](images/etsug_qlim0171.png)
The following table shows various functional forms of heteroscedasticity and the corresponding options to request each model.
|
No. |
Model |
Options |
|
|---|---|---|---|
|
1 |
|
LINK=EXP (default) |
|
|
2 |
|
LINK=EXP NOCONST |
|
|
3 |
|
LINK=LINEAR |
|
|
4 |
|
LINK=LINEAR SQUARE |
For discrete choice models, 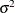 is normalized (
is normalized (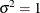 ) since this parameter is not identified. Note that in models 3 and 5, it may be possible that variances of some observations
are negative. Although the QLIM procedure assigns a large penalty to move the optimization away from such region, it is possible
that the optimization cannot improve the objective function value and gets locked in the region. Signs of such outcome include
extremely small likelihood values or missing standard errors in the estimates. In models 2 and 6, variances are guaranteed
to be greater or equal to zero, but it may be possible that variances of some observations are very close to zero. In these
scenarios, standard errors may be missing. Models 1 and 4 do not have such problems. Variances in these models are always
positive and never close to zero.
) since this parameter is not identified. Note that in models 3 and 5, it may be possible that variances of some observations
are negative. Although the QLIM procedure assigns a large penalty to move the optimization away from such region, it is possible
that the optimization cannot improve the objective function value and gets locked in the region. Signs of such outcome include
extremely small likelihood values or missing standard errors in the estimates. In models 2 and 6, variances are guaranteed
to be greater or equal to zero, but it may be possible that variances of some observations are very close to zero. In these
scenarios, standard errors may be missing. Models 1 and 4 do not have such problems. Variances in these models are always
positive and never close to zero.
The heteroscedastic regression model is estimated using the following log-likelihood function:
![\[ \ell = -\frac{N}{2}\ln (2\pi ) - \sum _{i=1}^{N}\frac{1}{2}\ln (\sigma _{i}^{2}) - \frac{1}{2}\sum _{i=1}^{N} (\frac{e_{i}}{\sigma _{i}})^{2} \]](images/etsug_qlim0178.png)
where 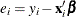 .
.
Box-Cox Modeling
The Box-Cox transformation on x is defined as
![\[ x^{(\lambda )} = \left\{ \begin{array}{ll} \frac{x^{\lambda }-1}{\lambda } & \mr{if} \lambda \neq 0 \\ \ln (x) & \mr{if} \lambda = 0 \end{array} \right. \]](images/etsug_qlim0180.png)
The Box-Cox regression model with heteroscedasticity is written as
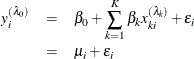
where 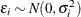 and transformed variables must be positive. In practice, too many transformation parameters cause numerical problems in model
fitting. It is common to have the same Box-Cox transformation performed on all the variables — that is,
and transformed variables must be positive. In practice, too many transformation parameters cause numerical problems in model
fitting. It is common to have the same Box-Cox transformation performed on all the variables — that is, 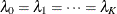 . It is required for the magnitude of transformed variables to be in the tolerable range if the corresponding transformation
parameters are
. It is required for the magnitude of transformed variables to be in the tolerable range if the corresponding transformation
parameters are 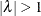 .
.
The log-likelihood function of the Box-Cox regression model is written as
![\[ \ell = -\frac{N}{2}\ln (2\pi ) - \sum _{i=1}^{N}\ln (\sigma _{i}) - \frac{1}{2\sigma _{i}^{2}}\sum _{i=1}^{N}e_{i}^{2} + (\lambda _{0}-1)\sum _{i=1}^{N}\ln (y_{i}) \]](images/etsug_qlim0185.png)
where 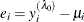 .
.
When the dependent variable is discrete, censored, or truncated, the Box-Cox transformation can be applied only to explanatory variables.