The QLIM Procedure

Limited Dependent Variable Models

Subsections:

Censored Regression Models

When the dependent variable is censored, values in a certain range are all transformed to a single value. For example, the standard tobit model can be defined as

\[ y^{*}_{i} = \mathbf{x}_{i}’\bbeta + \epsilon _{i} \]
\[ y_{i} = \left\{ \begin{array}{ll} y^{*}_{i} & \mr{if} y^{*}_{i}>0 \\ 0 & \mr{if} y^{*}_{i}\leq 0 \end{array} \right. \]

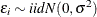where $\epsilon _{i} \sim iid N(0,\sigma ^{2})$. The log-likelihood function of the standard censored regression model is

\[ \ell = \sum _{i\in \{ y_{i}=0\} }\ln [1-\Phi (\mathbf{x}_{i}’\bbeta /\sigma )] +\sum _{i\in \{ y_{i}>0\} } \ln \left[\phi (\frac{y_{i}-\mathbf{x}_{i}'\bbeta }{\sigma })/\sigma \right] \]

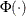where $\Phi (\cdot )$ is the cumulative density function of the standard normal distribution and 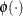$\phi (\cdot )$ is the probability density function of the standard normal distribution.

The tobit model can be generalized to handle observation-by-observation censoring. The censored model on both of the lower and upper limits can be defined as

\[ y_{i} = \left\{ \begin{array}{ll} R_{i} & \mr{if} \; y_{i}^{*} \geq R_{i} \\ y_{i}^{*} & \mr{if} \; L_{i} < y_{i}^{*} < R_{i} \\ L_{i} & \mr{if} \; y_{i}^{*} \leq L_{i} \end{array} \right. \]

The log-likelihood function can be written as

\begin{eqnarray*} \ell & = & \sum _{i\in \{ L_{i}< y_{i} < R_{i}\} } \ln \left[\phi (\frac{y_{i}-\mathbf{x}_{i}'\bbeta }{\sigma })/\sigma \right] + \sum _{i\in \{ y_{i}=R_{i}\} } \ln \left[\Phi (-\frac{R_{i}-\mathbf{x}_{i}'\bbeta }{\sigma })\right] + \\ & & \sum _{i\in \{ y_{i}=L_{i}\} } \ln \left[\Phi (\frac{L_{i}-\mathbf{x}_{i}'\bbeta }{\sigma })\right] \end{eqnarray*}

Log-likelihood functions of the lower- or upper-limit censored model are easily derived from the two-limit censored model. The log-likelihood function of the lower-limit censored model is

\[ \ell = \sum _{i\in \{ y_{i} > L_{i}\} } \ln \left[\phi (\frac{y_{i}-\mathbf{x}_{i}'\bbeta }{\sigma })/\sigma \right] + \sum _{i\in \{ y_{i}=L_{i}\} } \ln \left[\Phi (\frac{L_{i}-\mathbf{x}_{i}'\bbeta }{\sigma })\right] \]

The log-likelihood function of the upper-limit censored model is

\[ \ell = \sum _{i\in \{ y_{i} < R_{i}\} } \ln \left[\phi (\frac{y_{i}-\mathbf{x}_{i}'\bbeta }{\sigma })/\sigma \right] + \sum _{i\in \{ y_{i}=R_{i}\} } \ln \left[1-\Phi (\frac{R_{i}- \mathbf{x}_{i}'\bbeta }{\sigma })\right] \]

Types of Tobit Models

Amemiya (1984) classified Tobit models into five types based on characteristics of the likelihood function. For notational convenience, let P denote a distribution or density function, $y^{*}_{ji}$ is assumed to be normally distributed with mean $\mathbf{x}_{ji}’\bbeta _{j}$ and variance $\sigma ^{2}_{j}$.

Type 1 Tobit

The Type 1 Tobit model was already discussed in the preceding section.

\begin{eqnarray*} y_{1i}^{*} & = & \mathbf{x}_{1i}’\bbeta _{1} + u_{1i} \\ y_{1i} & = & y_{1i}^{*}\; \; \; \textrm{if $y^{*}_{1i} > 0$} \\ & = & 0 \; \; \; \textrm{if $y^{*}_{1i} \leq 0$} \end{eqnarray*}

The likelihood function is characterized as $P(y_{1} < 0)P(y_{1})$.

Type 2 Tobit

The Type 2 Tobit model is defined as

\begin{eqnarray*} y_{1i}^{*} & = & \mathbf{x}_{1i}’\bbeta _{1} + u_{1i} \\ y_{2i}^{*} & = & \mathbf{x}_{2i}’\bbeta _{2} + u_{2i} \\ y_{1i} & = & 1 \; \; \; \textrm{if $y_{1i}^{*}>0$} \\ & = & 0 \; \; \; \textrm{if $y_{1i}^{*}\leq 0$} \\ y_{2i} & = & y_{2i}^{*} \; \; \; \textrm{if $y_{1i}^{*}>0$} \\ & = & 0 \; \; \; \textrm{if $y_{1i}^{*}\leq 0$} \end{eqnarray*}

where $(u_{1i},u_{2i}) \sim N(0,\Sigma )$. The likelihood function is described as $P(y_{1} < 0)P(y_{1}>0,y_{2})$.

Type 3 Tobit

The Type 3 Tobit model is different from the Type 2 Tobit in that $y_{1i}^{*}$ of the Type 3 Tobit is observed when $y_{1i}^{*}>0$.

\begin{eqnarray*} y_{1i}^{*} & = & \mathbf{x}_{1i}’\bbeta _{1} + u_{1i} \\ y_{2i}^{*} & = & \mathbf{x}_{2i}’\bbeta _{2} + u_{2i} \\ y_{1i} & = & y_{1i}^{*}\; \; \; \textrm{if $y^{*}_{1i} > 0$} \\ & = & 0 \; \; \; \textrm{if $y^{*}_{1i} \leq 0$} \\ y_{2i} & = & y_{2i}^{*}\; \; \; \textrm{if $y^{*}_{1i} > 0$} \\ & = & 0 \; \; \; \textrm{if $y^{*}_{1i} \leq 0$} \end{eqnarray*}

where $(u_{1i},u_{2i})’\sim iid N(0,\Sigma )$.

The likelihood function is characterized as $P(y_{1} < 0)P(y_{1},y_{2})$. Type 4 Tobit

The Type 4 Tobit model consists of three equations:

\begin{eqnarray*} y_{1i}^{*} & = & \mathbf{x}_{1i}’\bbeta _{1} + u_{1i} \\ y_{2i}^{*} & = & \mathbf{x}_{2i}’\bbeta _{2} + u_{2i} \\ y_{3i}^{*} & = & \mathbf{x}_{3i}’\bbeta _{3} + u_{3i} \\ y_{1i} & = & y_{1i}^{*}\; \; \; \textrm{if $y^{*}_{1i} > 0$} \\ & = & 0 \; \; \; \textrm{if $y^{*}_{1i} \leq 0$} \\ y_{2i} & = & y_{2i}^{*}\; \; \; \textrm{if $y^{*}_{1i} > 0$} \\ & = & 0 \; \; \; \textrm{if $y^{*}_{1i} \leq 0$} \\ y_{3i} & = & y_{3i}^{*}\; \; \; \textrm{if $y^{*}_{1i} \leq 0$} \\ & = & 0 \; \; \; \textrm{if $y^{*}_{1i} > 0$} \end{eqnarray*}

where $(u_{1i},u_{2i},u_{3i})’\sim iid N(0,\Sigma )$. The likelihood function of the Type 4 Tobit model is characterized as $P(y_{1} < 0, y_{3})P(y_{1},y_{2})$.

Type 5 Tobit

The Type 5 Tobit model is defined as follows:

\begin{eqnarray*} y_{1i}^{*} & = & \mathbf{x}_{1i}’\bbeta _{1} + u_{1i} \\ y_{2i}^{*} & = & \mathbf{x}_{2i}’\bbeta _{2} + u_{2i} \\ y_{3i}^{*} & = & \mathbf{x}_{3i}’\bbeta _{3} + u_{3i} \\ y_{1i} & = & 1\; \; \; \textrm{if $y^{*}_{1i} > 0$} \\ & = & 0\; \; \; \textrm{if $y^{*}_{1i} \leq 0$} \\ y_{2i} & = & y_{2i}^{*}\; \; \; \textrm{if $y^{*}_{1i} > 0$} \\ & = & 0 \; \; \; \textrm{if $y^{*}_{1i} \leq 0$} \\ y_{3i} & = & y_{3i}^{*}\; \; \; \textrm{if $y^{*}_{1i} \leq 0$} \\ & = & 0 \; \; \; \textrm{if $y^{*}_{1i} > 0$} \end{eqnarray*}

where $(u_{1i},u_{2i},u_{3i})’$ are from iid trivariate normal distribution. The likelihood function of the Type 5 Tobit model is characterized as $P(y_{1} < 0, y_{3})P(y_{1} > 0, y_{2})$.

Code examples for these models can be found in Types of Tobit Models.

Truncated Regression Models

In a truncated model, the observed sample is a subset of the population where the dependent variable falls in a certain range. For example, when neither a dependent variable nor exogenous variables are observed for $y^{*}_{i} < 0$, the truncated regression model can be specified.

\[ \ell = \sum _{i\in \{ y_{i}\geq 0\} } \left\{ -\ln \Phi (\mathbf{x}_{i}’\bbeta /\sigma ) + \ln \left[\frac{\phi ((y_{i} - \mathbf{x}_{i}'\bbeta )/\sigma )}{\sigma } \right] \right\} \]

Two-limit truncation model is defined as

\[ y_{i} = y_{i}^{*} \mr{if} \; L_{i} \leq y_{i}^{*} \leq R_{i} \]

The log-likelihood function of the two-limit truncated regression model is

\[ \ell = \sum _{i=1}^{N} \left\{ \ln \left[\phi (\frac{y_{i}-\mathbf{x}_{i}'\bbeta }{\sigma })/\sigma \right] - \ln \left[\Phi (\frac{R_{i}-\mb{x}_{i}'\bbeta }{\sigma }) - \Phi (\frac{L_{i}-\mb{x}_{i}'\bbeta }{\sigma })\right] \right\} \]

The log-likelihood functions of the lower- and upper-limit truncation model are

\begin{eqnarray*} \ell & = & \sum _{i=1}^{N}\left\{ \ln \left[\phi (\frac{y_{i}-\mb{x}_{i}'\bbeta }{\sigma }) / \sigma \right] - \ln \left[1 - \Phi (\frac{L_{i}-\mb{x}_{i}'\bbeta }{\sigma })\right] \right\} \; \; \textrm{(lower)} \\ \ell & = & \sum _{i=1}^{N}\left\{ \ln \left[\phi (\frac{y_{i}-\mb{x}_{i}'\bbeta }{\sigma }) / \sigma \right] - \ln \left[\Phi (\frac{R_{i}-\mb{x}_{i}'\bbeta }{\sigma })\right] \right\} \; \; \textrm{(upper)} \end{eqnarray*}