The PANEL Procedure
- Overview
- Getting Started
-
Syntax
-
DetailsSpecifying the Input DataSpecifying the Regression ModelUnbalanced DataMissing ValuesComputational ResourcesRestricted EstimatesNotationOne-Way Fixed-Effects ModelTwo-Way Fixed-Effects ModelBalanced PanelsUnbalanced PanelsFirst-Differenced Methods for One-Way and Two-Way ModelsBetween EstimatorsPooled EstimatorOne-Way Random-Effects ModelTwo-Way Random-Effects ModelHausman-Taylor EstimationAmemiya-MaCurdy EstimationParks Method (Autoregressive Model)Da Silva Method (Variance-Component Moving Average Model)Dynamic Panel EstimatorsLinear Hypothesis TestingHeteroscedasticity-Corrected Covariance MatricesHeteroscedasticity- and Autocorrelation-Consistent Covariance MatricesR-SquareSpecification TestsPanel Data Poolability TestPanel Data Cross-Sectional Dependence TestPanel Data Unit Root TestsLagrange Multiplier (LM) Tests for Cross-Sectional and Time EffectsTests for Serial Correlation and Cross-Sectional EffectsTroubleshootingCreating ODS GraphicsOUTPUT OUT= Data SetOUTEST= Data SetOUTTRANS= Data SetPrinted OutputODS Table Names
-
Examples
- References
Getting Started: PANEL Procedure
The following statements use the cost function data from Greene (1990) to estimate a variance components model. The variable PRODUCTION is the log of output in millions of kilowatt-hours, and COST is the log of cost in millions of dollars. See Greene (1990) for details.
data greene; input firm year production cost @@; datalines; 1 1955 5.36598 1.14867 1 1960 6.03787 1.45185 1 1965 6.37673 1.52257 1 1970 6.93245 1.76627 2 1955 6.54535 1.35041 2 1960 6.69827 1.71109 2 1965 7.40245 2.09519 2 1970 7.82644 2.39480 3 1955 8.07153 2.94628 3 1960 8.47679 3.25967 ... more lines ...
You decide to fit the following model to the data:
![\[ C_{it}= \mr{Intercept} + {\bbeta }P_{it}+v_{i}+e_{t}+{\epsilon }_{it} \; \; i=1, {\ldots }, \mi{N} ; \; t=1, {\ldots }, \mi{T} \]](images/etsug_panel0001.png)
where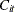 
and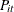 
represent the cost and production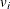, 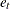and 
, 
and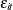 
are the cross-sectional, time series, and error variance components.
If you assume that the time and cross-sectional effects are random, you are left with four possible estimators for the variance components. You choose Fuller-Battese.
The following statements fit this model:
proc sort data=greene; by firm year; run; proc panel data=greene; model cost = production / rantwo vcomp = fb; id firm year; run;
The PANEL procedure output is shown in Figure 27.1. A model description is printed first, which reports the estimation method used and the number of cross sections and time periods. Fit statistics and variance components estimates are printed next. A Hausman specification test compares this model to its fixed-effects analog. Finally, the table of regression parameter estimates shows the estimates, standard errors, and t tests.
Figure 27.1: The Variance Components Estimates