The PANEL Procedure
- Overview
- Getting Started
-
Syntax

-
Details
 Specifying the Input DataSpecifying the Regression ModelUnbalanced DataMissing ValuesComputational ResourcesRestricted EstimatesNotationOne-Way Fixed-Effects ModelTwo-Way Fixed-Effects ModelBalanced PanelsUnbalanced PanelsFirst-Differenced Methods for One-Way and Two-Way ModelsBetween EstimatorsPooled EstimatorOne-Way Random-Effects ModelTwo-Way Random-Effects ModelHausman-Taylor EstimationAmemiya-MaCurdy EstimationParks Method (Autoregressive Model)Da Silva Method (Variance-Component Moving Average Model)Dynamic Panel EstimatorsLinear Hypothesis TestingHeteroscedasticity-Corrected Covariance MatricesHeteroscedasticity- and Autocorrelation-Consistent Covariance MatricesR-SquareSpecification TestsPanel Data Poolability TestPanel Data Cross-Sectional Dependence TestPanel Data Unit Root TestsLagrange Multiplier (LM) Tests for Cross-Sectional and Time EffectsTests for Serial Correlation and Cross-Sectional EffectsTroubleshootingCreating ODS GraphicsOUTPUT OUT= Data SetOUTEST= Data SetOUTTRANS= Data SetPrinted OutputODS Table Names
Specifying the Input DataSpecifying the Regression ModelUnbalanced DataMissing ValuesComputational ResourcesRestricted EstimatesNotationOne-Way Fixed-Effects ModelTwo-Way Fixed-Effects ModelBalanced PanelsUnbalanced PanelsFirst-Differenced Methods for One-Way and Two-Way ModelsBetween EstimatorsPooled EstimatorOne-Way Random-Effects ModelTwo-Way Random-Effects ModelHausman-Taylor EstimationAmemiya-MaCurdy EstimationParks Method (Autoregressive Model)Da Silva Method (Variance-Component Moving Average Model)Dynamic Panel EstimatorsLinear Hypothesis TestingHeteroscedasticity-Corrected Covariance MatricesHeteroscedasticity- and Autocorrelation-Consistent Covariance MatricesR-SquareSpecification TestsPanel Data Poolability TestPanel Data Cross-Sectional Dependence TestPanel Data Unit Root TestsLagrange Multiplier (LM) Tests for Cross-Sectional and Time EffectsTests for Serial Correlation and Cross-Sectional EffectsTroubleshootingCreating ODS GraphicsOUTPUT OUT= Data SetOUTEST= Data SetOUTTRANS= Data SetPrinted OutputODS Table Names -
Examples

- References
Panel Data Poolability Test
The null hypothesis of poolability assumes homogeneous slope coefficients. An F test can be applied to test for the poolability across cross sections in panel data models.
F Test
For the unrestricted model, run a regression for each cross section and save the sum of squared residuals as 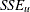 . For the restricted model, save the sum of squared residuals as
. For the restricted model, save the sum of squared residuals as 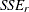 . If the test applies to all coefficients (including the constant), then the restricted model is the pooled model (OLS); if
the test applies to coefficients other than the constant, then the restricted model is the fixed one-way model with cross-sectional
fixed effects. If N and T denote the number of cross sections and time periods, then the number of observations is
. If the test applies to all coefficients (including the constant), then the restricted model is the pooled model (OLS); if
the test applies to coefficients other than the constant, then the restricted model is the fixed one-way model with cross-sectional
fixed effects. If N and T denote the number of cross sections and time periods, then the number of observations is 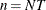 .[7] Let k be the number of regressors except the constant. The degree of freedom for the unrestricted model is
.[7] Let k be the number of regressors except the constant. The degree of freedom for the unrestricted model is 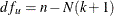 . If the constant is restricted to be the same, the degree of freedom for the restricted model is
. If the constant is restricted to be the same, the degree of freedom for the restricted model is 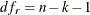 and the number of restrictions is
and the number of restrictions is 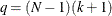 . If the restricted model is the fixed one-way model, the degree of freedom is
. If the restricted model is the fixed one-way model, the degree of freedom is 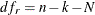 and the number of restrictions is
and the number of restrictions is 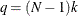 . So the F test is
. So the F test is
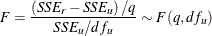
For large N and T, you can use a chi-square distribution to approximate the limiting distribution, namely, 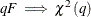 . The error term is assumed to be homogeneous; therefore,
. The error term is assumed to be homogeneous; therefore, 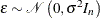 , and an OLS regression is sufficient. The test is the same as the Chow test (Chow 1960) extended to N linear regressions.
, and an OLS regression is sufficient. The test is the same as the Chow test (Chow 1960) extended to N linear regressions.
LR Test
Zellner (1962) also proved that the likelihood ratio test for null hypothesis of poolability can be based on the F statistic. The likelihood ratio can be expressed as 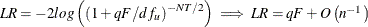 . Under
. Under 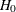 ,
, 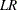 is asymptotically distributed as a chi-square with q degrees of freedom.
is asymptotically distributed as a chi-square with q degrees of freedom.
[7] For the unbalanced panel, the number of time series 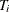 might be different. The number of observations needs to be redefined accordingly.
might be different. The number of observations needs to be redefined accordingly.