The PANEL Procedure

Amemiya-MaCurdy Estimation

The Amemiya and MaCurdy (1986) model is similar to the Hausman-Taylor model. Following the development in the section Hausman-Taylor Estimation, estimation is identical up to the final 2SLS instrumental variables regression. In addition to the set of instruments used by the Hausman-Taylor estimator, use the following:

  • $\Strong{X}_{1i1}, \Strong{X}_{1i2}, \ldots , \Strong{X}_{1iT}$

For each observation in the ith cross section, you use the data on the time-varying exogenous regressors for the entire cross section. Because of the structure of the added instruments, the Amemiya-MaCurdy estimator can be applied only to balanced data.

The Amemiya-MaCurdy model attempts to gain efficiency over Hausman-Taylor by adding instruments. This comes at a price of a more stringent assumption on the exogeneity of the 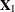$\Strong{X}_1$ variables. Although the Hausman-Taylor model requires only that the cross-sectional means of 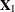$\Strong{X}_1$ be orthogonal to 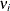$\nu _ i$, the Amemiya-MaCurdy estimation requires orthogonality at every point in time; see Baltagi (2008, sec. 7.4).

A Hausman specification test is provided to test the validity of the added assumption. Define 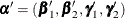$\balpha ’ = (\bbeta ’_1, \bbeta ’_2, \bgamma ’_1, \bgamma ’_2)$, its Hausman-Taylor estimate as 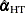$\hat\balpha _{\mr{HT}}$, and its Amemiya-MaCurdy estimate as 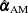$\hat\balpha _{\mr{AM}}$. Under the null hypothesis, both estimators are consistent and 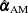$\hat\balpha _{\mr{AM}}$ is efficient. The Hausman test statistic is then

\[ m = \left(\hat\balpha _{\mr{HT}}-\hat\balpha _{\mr{AM}} \right)’ \left(\hat{\Strong{S}}_{\mr{HT}}-\hat{\Strong{S}}_{\mr{AM}}\right)^{-1} \left(\hat\balpha _{\mr{HT}} - \hat\balpha _{\mr{AM}}\right) \]

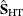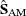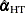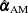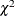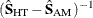where $\hat{\Strong{S}}_{\mr{HT}}$ and $\hat{\Strong{S}}_{\mr{AM}}$ are variance-covariance estimates of $\hat\balpha _{\mr{HT}}$ and $\hat\balpha _{\mr{AM}}$, respectively. Under the null hypothesis, m is distributed as $\chi ^2$ with degrees of freedom equal to the rank of $(\hat{\Strong{S}}_{\mr{HT}} - \hat{\Strong{S}}_{\mr{AM}})^{-1}$.