The PANEL Procedure

Parks Method (Autoregressive Model)

Subsections:

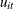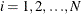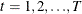Parks (1967) considered the first-order autoregressive model in which the random errors ${u_{it} }$, ${i=1, 2, {\ldots }, \mi{N} }$, and ${t=1, 2, {\ldots }, \mi{T} }$ have the structure

\begin{eqnarray*} {E}( u^{2}_{it})& =& {\sigma }_{ii} \textrm{(heteroscedasticity)} \\ {E}(u_{it}u_{jt})& =& {\sigma }_{ij} \textrm{(contemporaneously correlated)} \\ u_{it}& =& {\rho }_{i} u_{i,t-1}+ {\epsilon }_{it} \textrm{(autoregression)} \nonumber \end{eqnarray*}

where

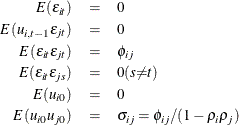
\begin{eqnarray*} {E}( {\epsilon }_{it})& =& 0 \\ {E}( u_{i,t-1} {\epsilon }_{jt})& =& 0 \\ {E}( {\epsilon }_{it} {\epsilon }_{jt})& =& {\phi }_{ij} \\ {E}( {\epsilon }_{it} {\epsilon }_{js})& =& 0 (s{\neq }t) \\ {E}( u_{i0})& =& 0 \\ {E}( u_{i0} u_{j0})& =& {\sigma }_{ij}={\phi }_{ij}/(1- {\rho }_{i} {\rho }_{j}) \nonumber \end{eqnarray*}

The model assumed is first-order autoregressive with contemporaneous correlation between cross sections. In this model, the covariance matrix for the vector of random errors u can be expressed as

\begin{eqnarray*} {E}( \Strong{uu} ^{'})=\Strong{V} = \left[\begin{matrix} {\sigma }_{11}P_{11} & {\sigma }_{12}P_{12} & {\ldots } & {\sigma }_{1N}P_{1N} \\ {\sigma }_{21}P_{21} & {\sigma }_{22}P_{22} & {\ldots } & {\sigma }_{2N}P_{2N} \\ {\vdots } & {\vdots } & {\vdots } & {\vdots } \\ {\sigma }_{N1}P_{N1} & {\sigma }_{N2}P_{N2} & {\ldots } & {\sigma }_{NN}P_{NN} \\ \end{matrix} \nonumber \right] \end{eqnarray*}

where

\begin{eqnarray*} P_{ij}= \left[\begin{matrix} 1 & {\rho }_{j} & {\rho }_{j}^{2} & {\ldots } & {\rho }^{T-1}_{j} \\ {\rho }_{i} & 1 & {\rho }_{j} & {\ldots } & {\rho }^{T-2}_{j} \\ {\rho }_{i}^{2} & {\rho }_{i} & 1 & {\ldots } & {\rho }^{T-3}_{j} \\ {\vdots } & {\vdots } & {\vdots } & {\vdots } & {\vdots } \\ {\rho }^{T-1}_{i} & {\rho }^{T-2}_{i} & {\rho }^{T-3}_{i} & {\ldots } & 1 \\ \end{matrix} \nonumber \right] \end{eqnarray*}

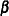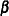The matrix V is estimated by a two-stage procedure, and $\bbeta $ is then estimated by generalized least squares. The first step in estimating V involves the use of ordinary least squares to estimate $\bbeta $ and obtain the fitted residuals, as follows:

\[ \hat{\mb{u}} =\mb{y}-\mb{X} \hat{\bbeta }_{OLS} \]

A consistent estimator of the first-order autoregressive parameter is then obtained in the usual manner, as follows:

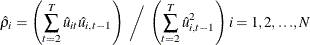
\begin{eqnarray*} \hat{\rho }_{i}= \left(\sum _{t=2}^{T} \hat{u}_{it} \hat{u}_{i,t-1}\right) ~ \bigg/~ \left(\sum _{t=2}^{T}{\hat{u}^{2}_{i,t-1}}\right) i=1, 2, {\ldots }, \emph{N} \nonumber \end{eqnarray*}

Finally, the autoregressive characteristic of the data is removed (asymptotically) by the usual transformation of taking weighted differences. That is, for 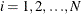${i=1,2,{\ldots },\mi{N} }$,

\[ y_{i1}\sqrt {1- \hat{\rho }^{2}_{i}}= \sum _{k=1}^{p}{X_{i1k}\mb{{\bbeta }}_{k}} \sqrt {1- \hat{\rho }^{2}_{i}} +u_{i1}\sqrt {1- \hat{\rho }^{2}_{i}} \]
\[ y_{it}- \hat{\rho }_{i} y_{i,t-1} =\sum _{k=1}^{p}{( X_{itk}- \hat{\rho }_{i} \mb{X} _{i,t-1,k}) {\bbeta }_{k}} + u_{it}- \hat{\rho }_{i} u_{i,t-1} t=2,{\ldots },\mi{T} \]

which is written

\[ y^{\ast }_{it}= \sum _{k=1}^{p}{X^{\ast }_{itk} {\bbeta }_{k}}+ u^{\ast }_{it} \; \; i=1, 2, {\ldots }, \mi{N} ; \; \; t=1, 2, {\ldots }, \mi{T} \]

Notice that the transformed model has not lost any observations (Seely and Zyskind 1971).

The second step in estimating the covariance matrix V is applying ordinary least squares to the preceding transformed model, obtaining

\[ \hat{\mb{u}} ^{\ast }= \mb{y} ^{\ast }- \mb{X} ^{\ast } {\bbeta }^{\ast }_{OLS} \]

from which the consistent estimator of ${\sigma }$$_{ij}$ is calculated as follows:

\[ s_{ij}=\frac{\hat{\phi }_{ij}}{(1- \hat{\rho }_{i} \hat{\rho }_{j}) } \]

where

\[ \hat{\phi }_{ij}=\frac{1}{(\mi{T} -p)} \sum _{t=1}^{T} \hat{u}^{\ast }_{it} \hat{u}^{\ast }_{jt} \]

Estimated generalized least squares (EGLS) then proceeds in the usual manner,

\[ \hat{\bbeta }_{P}= ({\mb{X} ’}\hat{\mb{V}} ^{-1}\mb{X} )^{-1} {\mb{X} ’}\hat{\mb{V}} ^{-1}\mb{y} \]

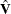where $\hat{\mb{V}}$ is the derived consistent estimator of V. For computational purposes, 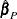${\hat{\bbeta }_{P}}$ is obtained directly from the transformed model,

\[ \hat{\bbeta }_{P}= ({\mb{X} ^{\ast '}}(\hat{\Phi }^{-1}{\otimes }I_{T}) \mb{X} ^{\ast })^{-1}{\mb{X} ^{\ast '}} (\hat{\Phi }^{-1}{\otimes }I_{T}) \mb{y} ^{\ast } \]

where ${\hat{\Phi }= [\hat{\phi }_{ij}]_{i,j=1,{\ldots },N} }$.

The preceding procedure is equivalent to Zellner’s two-stage methodology applied to the transformed model (Zellner 1962).

Parks demonstrates that this estimator is consistent and asymptotically, normally distributed with

\[ \mr{Var}(\hat{\bbeta }_{P})= ({\mb{X} ’}\mb{V} ^{-1}\mb{X} )^{-1} \]

Standard Corrections

For the PARKS option, the first-order autocorrelation coefficient must be estimated for each cross section. Let 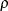${\rho }$ be the 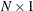${\mi{N} \times 1}$ vector of true parameters and 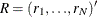${R=(r_{1},{\ldots },r_{N}{)’} }$ be the corresponding vector of estimates. Then, to ensure that only range-preserving estimates are used in PROC PANEL, the following modification for R is made:

\[ r_{i} = \begin{cases} r_{i} & \mr{if} \hspace{.1 in}{|r_{i}|}<1 \\ \mr{max}(.95, \mr{rmax}) & \mr{if}\hspace{.1 in} r_{i}{\ge }1 \\ \mr{min}(-.95, \mr{rmin}) & \mr{if}\hspace{.1 in} r_{i}{\le }-1 \end{cases} \]

where

\[ \mr{rmax} = \begin{cases} 0 & \mr{if}\hspace{.1 in} r_{i} < 0 \hspace{.1 in}\mr{or}\hspace{.1 in} r_{i}{\ge }1\hspace{.1 in} \forall i \\ \mathop {\mr{max}}\limits _{j} [ r_{j} : 0 {\le } r_{j} < 1 ] & \mr{otherwise} \end{cases} \]

and

\[ \mr{rmin }= \begin{cases} 0 & \mr{if} \hspace{.1 in}r_{i} > 0 \hspace{.1 in}\mr{or}\hspace{.1 in} r_{i}{\le }-1\hspace{.1 in} \forall i \\ \mathop {\mr{max}}\limits _{j} [ r_{j} : -1 < r_{j} {\le } 0 ] & \mr{otherwise} \end{cases} \]

Whenever this correction is made, a warning message is printed.