The PANEL Procedure
- Overview
- Getting Started
-
Syntax

-
Details
 Specifying the Input DataSpecifying the Regression ModelUnbalanced DataMissing ValuesComputational ResourcesRestricted EstimatesNotationOne-Way Fixed-Effects ModelTwo-Way Fixed-Effects ModelBalanced PanelsUnbalanced PanelsFirst-Differenced Methods for One-Way and Two-Way ModelsBetween EstimatorsPooled EstimatorOne-Way Random-Effects ModelTwo-Way Random-Effects ModelHausman-Taylor EstimationAmemiya-MaCurdy EstimationParks Method (Autoregressive Model)Da Silva Method (Variance-Component Moving Average Model)Dynamic Panel EstimatorsLinear Hypothesis TestingHeteroscedasticity-Corrected Covariance MatricesHeteroscedasticity- and Autocorrelation-Consistent Covariance MatricesR-SquareSpecification TestsPanel Data Poolability TestPanel Data Cross-Sectional Dependence TestPanel Data Unit Root TestsLagrange Multiplier (LM) Tests for Cross-Sectional and Time EffectsTests for Serial Correlation and Cross-Sectional EffectsTroubleshootingCreating ODS GraphicsOUTPUT OUT= Data SetOUTEST= Data SetOUTTRANS= Data SetPrinted OutputODS Table Names
Specifying the Input DataSpecifying the Regression ModelUnbalanced DataMissing ValuesComputational ResourcesRestricted EstimatesNotationOne-Way Fixed-Effects ModelTwo-Way Fixed-Effects ModelBalanced PanelsUnbalanced PanelsFirst-Differenced Methods for One-Way and Two-Way ModelsBetween EstimatorsPooled EstimatorOne-Way Random-Effects ModelTwo-Way Random-Effects ModelHausman-Taylor EstimationAmemiya-MaCurdy EstimationParks Method (Autoregressive Model)Da Silva Method (Variance-Component Moving Average Model)Dynamic Panel EstimatorsLinear Hypothesis TestingHeteroscedasticity-Corrected Covariance MatricesHeteroscedasticity- and Autocorrelation-Consistent Covariance MatricesR-SquareSpecification TestsPanel Data Poolability TestPanel Data Cross-Sectional Dependence TestPanel Data Unit Root TestsLagrange Multiplier (LM) Tests for Cross-Sectional and Time EffectsTests for Serial Correlation and Cross-Sectional EffectsTroubleshootingCreating ODS GraphicsOUTPUT OUT= Data SetOUTEST= Data SetOUTTRANS= Data SetPrinted OutputODS Table Names -
Examples

- References
Balanced Panels
Assume that the data are balanced (for example, all cross sections have T observations). Then you can write the following:
![\[ \tilde{\mi{y}}_\mi {it} = \mi{y_\mi {it}} - \bar{\mi{y}}_\mi {i \cdot } - \bar{\mi{y}}_\mi {\cdot t} + \bar{\bar{\mi{y}}} \]](images/etsug_panel0085.png)
![\[ \tilde{\mi{\mb{x}}}_\mi {it} = \mi{\mb{x} _\mi {it}} - \bar{\mi{\mb{x}}}_\mi {i \cdot } - \bar{\mi{\mb{x}}}_\mi {\cdot t} + \bar{\bar{\mi{\mb{x}}}} \]](images/etsug_panel0086.png)
where the symbols:
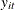 and
and 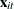 are the dependent variable (a scalar) and the explanatory variables (a vector whose columns are the explanatory variables
not including a constant), respectively
are the dependent variable (a scalar) and the explanatory variables (a vector whose columns are the explanatory variables
not including a constant), respectively
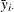 and
and 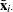 are cross section means
are cross section means
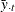 and
and 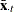 are time means
are time means
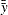 and
and 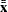 are the overall means
are the overall means
The two-way fixed-effects model is simply a regression of 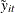 on
on 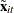 . Therefore, the two-way
. Therefore, the two-way 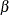 is given by:
is given by:
![\[ \tilde{{\beta }}_{s}= \left(\tilde{\mi{\mb{X}}}^{'}\tilde{\mi{\mb{X}}} \right)^{-1} \tilde{\mi{\mb{X}}}^{'}\tilde{\mb{y}} \]](images/etsug_panel0098.png)
The calculations of cross section dummy variables, time dummy variables, and intercepts follow in a fashion similar to that used in the one-way model.
First, you obtain the net cross-sectional and time effects. Denote the cross-sectional effects by 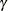 and the time effects by
and the time effects by  . These effects are calculated from the following relations:
. These effects are calculated from the following relations:
![\[ \hat{\gamma }_{i} = \left(\bar{\mi{y}}_\mi {i \cdot }- \bar{\bar{\mi{y}}} \right) - \tilde{{\beta }}_{s}\left( \bar{\mi{x}}_\mi {i \cdot }- \bar{\bar{\mi{x}}} \right) \]](images/etsug_panel0100.png)
![\[ \hat{\alpha }_{t} = \left(\bar{\mi{y}}_{\cdot \mi{t}}- \bar{\bar{\mi{y}}} \right) - \tilde{{\beta }}_{s}\left( \bar{\mi{x}}_{\cdot \mi{t}}- \bar{\bar{\mi{x}}} \right) \]](images/etsug_panel0101.png)
Denote the cross-sectional dummy variables and time dummy variables with the superscript C and T. Under the NOINT option the following equations give the dummy variables:
![\[ D_ i^{C} = \hat{\gamma }_{i} + \hat{\alpha }_{T} \]](images/etsug_panel0102.png)
![\[ D_ t^{T} = \hat{\alpha }_{t}- \hat{\alpha }_{T} \]](images/etsug_panel0103.png)
When an intercept is specified, the equations for dummy variables and intercept are:
![\[ D_ i^{C} = \hat{\gamma }_{i}- \hat{\gamma }_{N} \]](images/etsug_panel0104.png)
![\[ D_ t^{T} = \hat{\alpha }_{t}- \hat{\alpha }_{T} \]](images/etsug_panel0103.png)
![\[ \mr{Intercept }= \hat{\gamma }_{N} + \hat{\alpha }_{T} \]](images/etsug_panel0105.png)
The sum of squared errors is:
![\[ \mr{SSE}= \sum _\mi {i = 1} ^\mi {N} \sum _\mi {t = 1} ^\mi {T_\mi {i}} (y_\mi {it} - \gamma _\mi {i}-\alpha _\mi {t} - \mb{X} _{s}\tilde{{\beta }}_{s})^{2} \]](images/etsug_panel0106.png)
The estimated error variance is:
![\[ \hat{{\sigma }}_{{\epsilon }}^{2}= \mr{SSE }/ (\mi{M}-\mi{N}-\mi{T}-(\mi{K} -1)) \]](images/etsug_panel0107.png)
With or without a constant, the variance covariance matrix of 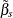 is given by:
is given by:
![\[ \mr{Var}\left[{\tilde{\beta }}_{s}\right] = \hat{{\sigma }}_{{\epsilon }}^{2}(\tilde{\mb{X} }^{'}_{s} \tilde{\mb{X} }_{s})^{-1} \]](images/etsug_panel0071.png)
Variance Covariance of Dummy Variables with No Intercept
The variances and covariances of the dummy variables are given with the NOINT specification as follows:
![\begin{eqnarray*} \mr{Var}\left(D_\emph {i} ^{C}\right) & =& \hat{\sigma }_{\epsilon }^{2} \left(\frac{1}{T} + \frac{1}{N} - \frac{1}{NT} \right) \\ & +& \left(\bar{\mi{\mb{x}}}_{\mi{i} \cdot } + \bar{\mi{\mb{x}}}_\mi {\cdot T} - \bar{\bar{\mi{\mb{x}}}}\right)^{'}\mr{Var}\left[{\tilde{\beta }}_{s}\right] \left(\bar{\mi{\mb{x}}}_\mi {i \cdot } + \bar{\mi{\mb{x}}}_\mi {\cdot T} - \bar{\bar{\mi{\mb{x}}}}\right) \end{eqnarray*}](images/etsug_panel0108.png)
![\[ \mr{Var}\left(D_\mi {t} ^{T}\right) = \frac{2\hat{\sigma }_{\epsilon }^{2}}{\mi{N}} +\left(\bar{\mi{\mb{x}}}_\mi {\cdot t} - \bar{\mi{\mb{x}}}_\mi {\cdot T}\right)^{'} \mr{Var}\left[{\tilde{\beta }}_{s}\right] \left( \bar{\mi{\mb{x}}}_\mi {\cdot t} - \bar{\mi{\mb{x}}}_\mi {\cdot T}\right) \]](images/etsug_panel0109.png)
![\begin{eqnarray*} \mr{Cov}\left(D_\emph {i} ^{C},D_\emph {j} ^{C}\right) & =& \hat{\sigma }_{\epsilon }^{2} \left(\frac{1}{N} - \frac{1}{NT} \right) \\ & +& \left(\bar{\mi{\mb{x}}}_\mi {i \cdot } + \bar{\mi{\mb{x}}}_\mi {\cdot t} - \bar{\bar{\mi{\mb{x}}}}\right)^{'}\mr{Var}\left[{\tilde{\beta }}_{s}\right] \left(\bar{\mi{\mb{x}}}_\mi {j \cdot } + \bar{\mi{\mb{x}}}_\mi {\cdot t} - \bar{\bar{\mi{\mb{x}}}}\right) \end{eqnarray*}](images/etsug_panel0110.png)
![\[ \mr{Cov}\left(D_\mi {t} ^{T},D_\mi {u} ^{T}\right) = \frac{\hat{\sigma }_{\epsilon }^{2}}{N} + \left(\bar{\mi{\mb{x}}}_\mi {\cdot t} - {\bar{\mi{\mb{x}}}}_{\cdot T}\right)^{'} \mr{Var}\left[{\tilde{\beta }}_{s}\right] \left( \bar{\mi{\mb{x}}}_\mi {\cdot u} - \bar{\mi{\mb{x}}}_{\cdot T}\right) \]](images/etsug_panel0111.png)
![\[ \mr{Cov}\left(D_\mi {i} ^{C},D_\mi {t} ^{T}\right) = -\frac{\hat{\sigma }_{\epsilon }^{2}}{N} +\left(\bar{\mi{\mb{x}}}_\mi {i \cdot } + \bar{\mi{\mb{x}}}_\mi {\cdot t} - \bar{\bar{\mi{\mb{x}}}}\right)^{'}\mr{Var}\left[{\tilde{\beta }}_{s}\right] \left( \bar{\mi{\mb{x}}}_\mi {\cdot t} - \bar{\mi{\mb{x}}}_{\cdot T}\right) \]](images/etsug_panel0112.png)
![\[ \mr{Cov}\left( D_\mi {i} ^ C,\beta \right) = -\left(\bar{\mi{\mb{x}}}_\mi {i \cdot } + \bar{\mi{\mb{x}}}_\mi {\cdot t} - \bar{\bar{\mi{\mb{x}}}}\right)^{'}\mr{Var}\left[{\tilde{\beta }}_{s}\right] \]](images/etsug_panel0113.png)
![\[ \mr{Cov}\left( D_\mi {i} ^ T,\beta \right) = -\left(\bar{\mi{\mb{x}}}_\mi {\cdot t} - \bar{\mi{\mb{x}}}_\mi {\cdot T}\right)^{'} \mr{Var}\left[{\tilde{\beta }}_{s}\right] \]](images/etsug_panel0114.png)
Variance Covariance of Dummy Variables with Intercept
The variances and covariances of the dummy variables are given when the intercept is included as follows:
![\begin{align*} \mr{Var}\left(D_\mi {i} ^{C}\right) & = \frac{2\hat{\sigma }_{\epsilon }^{2}}{T} +\left(\bar{\mi{\mb{x}}}_\mi {i \cdot } - \bar{\mi{\mb{x}}}_\mi {N \cdot }\right)^{'}\mr{Var}\left[{\tilde{\beta }}_{s}\right] \left(\bar{\mi{\mb{x}}}_\mi {i \cdot } - \bar{\mi{\mb{x}}}_\mi {N \cdot }\right)\\ \mr{Var}\left(D_\mi {t} ^{T}\right) & = \frac{2\hat{\sigma }_{\epsilon }^{2}}{\mi{N}} +\left(\bar{\mi{\mb{x}}}_\mi {\cdot t} - \bar{\mi{\mb{x}}}_\mi {\cdot T}\right)^{'} \mr{Var}\left[{\tilde{\beta }}_{s}\right] \left( \bar{\mi{\mb{x}}}_\mi {\cdot t} - \bar{\mi{\mb{x}}}_\mi {\cdot T}\right)\\ \mr{Var}\left(\mr{Intercept}\right) & = \hat{\sigma }_{\epsilon }^{2} \left(\frac{1}{T} + \frac{1}{N} - \frac{1}{NT} \right) +\left(\bar{\mi{\mb{x}}}_\mi {N \cdot } + \bar{\mi{\mb{x}}}_\mi {\cdot T} - \bar{\bar{\mi{\mb{x}}}}\right)^{'}\mr{Var}\left[{\tilde{\beta }}_{s}\right] \left(\bar{\mi{\mb{x}}}_\mi {N \cdot } + \bar{\mi{\mb{x}}}_\mi {\cdot T} - \bar{\bar{\mi{\mb{x}}}}\right)\\ \mr{Cov}\left(D_\mi {i} ^{C},D_\mi {j} ^{C}\right) & = \frac{\hat{\sigma }_{\epsilon }^{2}}{T} +\left(\bar{\mi{\mb{x}}}_\mi {i \cdot } - \bar{\mi{\mb{x}}}_\mi {N \cdot }\right)^{'}\mr{Var}\left[{\tilde{\beta }}_{s}\right] \left(\bar{\mi{\mb{x}}}_\mi {j \cdot } - \bar{\mi{\mb{x}}}_\mi {N \cdot }\right)\\ \mr{Cov}\left(D_\mi {t} ^{T},D_\mi {u} ^{T}\right) & = \frac{\hat{\sigma }_{\epsilon }^{2}}{N} +\left(\bar{\mi{\mb{x}}}_\mi {\cdot t} - \bar{\mi{\mb{x}}}_\mi {\cdot T}\right)^{'} \mr{Var}\left[{\tilde{\beta }}_{s}\right] \left( \bar{\mi{\mb{x}}}_\mi {\cdot u} - \bar{\mi{\mb{x}}}_\mi {\cdot T}\right)\\ \mr{Cov}\left(D_\mi {i} ^{C},D_\mi {u} ^{T}\right) & = \left(\bar{\mi{\mb{x}}}_\mi {i \cdot } - \bar{\mi{\mb{x}}}_\mi {N \cdot }\right)^{'} \mr{Var}\left[{\tilde{\beta }}_{s}\right] \left( \bar{\mi{\mb{x}}}_\mi {\cdot u} - \bar{\mi{\mb{x}}}_\mi {\cdot T}\right)\\ \mr{Cov}\left(D_\mi {i} ^{C},\mr{Intercept}\right) & =-\left(\frac{\hat{\sigma }_{\epsilon }^{2}}{T}\right) +\left(\bar{\mi{\mb{x}}}_\mi {i \cdot } - \bar{\mi{\mb{x}}}_\mi {N \cdot }\right)^{'} \mr{Var}\left({\tilde{\beta }}_{s}\right) \left(\bar{\mi{\mb{x}}}_\mi {N \cdot } + \bar{\mi{\mb{x}}}_\mi {\cdot T} - \bar{\bar{\mi{\mb{x}}}}\right) \\ \mr{Cov}\left(D_\mi {t} ^{T},\mr{Intercept}\right) & =-\left(\frac{\hat{\sigma }_{\epsilon }^{2}}{N}\right) +\left(\bar{\mi{\mb{x}}}_\mi {\cdot t} - \bar{\mi{\mb{x}}}_\mi {\cdot T}\right)^{'} \mr{Var}\left[{\tilde{\beta }}_{s}\right] \left(\bar{\mi{\mb{x}}}_\mi {N \cdot } + \bar{\mi{\mb{x}}}_\mi {\cdot T} - \bar{\bar{\mi{\mb{x}}}}\right) \\ \mr{Cov}\left(D_\mi {i} ^{C}, \tilde{\beta }\right) & =-\left(\bar{\mi{\mb{x}}}_\mi {i \cdot } - \bar{\mi{\mb{x}}}_\mi {N \cdot }\right)^{'}\mr{Var}\left[{\tilde{\beta }}_{s}\right] \\ \mr{Cov}\left(D_\mi {t} ^{T}, \tilde{\beta }\right) & =-\left(\bar{\mi{\mb{x}}}_\mi {\cdot t} - \bar{\mi{\mb{x}}}_\mi {\cdot T}\right)^{'} \mr{Var}\left[{\tilde{\beta }}_{s}\right] \\ \mr{Cov}\left(\mr{Intercept}, \tilde{\beta }\right) & =-\left(\bar{\mi{\mb{x}}}_\mi {N \cdot } + \bar{\mi{\mb{x}}}_\mi {\cdot T} - \bar{\bar{\mi{\mb{x}}}}\right)^{'}\mr{Var}\left[{\tilde{\beta }}_{s}\right] \end{align*}](images/etsug_panel0115.png)