The PANEL Procedure
- Overview
- Getting Started
-
Syntax

-
Details
 Specifying the Input DataSpecifying the Regression ModelUnbalanced DataMissing ValuesComputational ResourcesRestricted EstimatesNotationOne-Way Fixed-Effects ModelTwo-Way Fixed-Effects ModelBalanced PanelsUnbalanced PanelsFirst-Differenced Methods for One-Way and Two-Way ModelsBetween EstimatorsPooled EstimatorOne-Way Random-Effects ModelTwo-Way Random-Effects ModelHausman-Taylor EstimationAmemiya-MaCurdy EstimationParks Method (Autoregressive Model)Da Silva Method (Variance-Component Moving Average Model)Dynamic Panel EstimatorsLinear Hypothesis TestingHeteroscedasticity-Corrected Covariance MatricesHeteroscedasticity- and Autocorrelation-Consistent Covariance MatricesR-SquareSpecification TestsPanel Data Poolability TestPanel Data Cross-Sectional Dependence TestPanel Data Unit Root TestsLagrange Multiplier (LM) Tests for Cross-Sectional and Time EffectsTests for Serial Correlation and Cross-Sectional EffectsTroubleshootingCreating ODS GraphicsOUTPUT OUT= Data SetOUTEST= Data SetOUTTRANS= Data SetPrinted OutputODS Table Names
Specifying the Input DataSpecifying the Regression ModelUnbalanced DataMissing ValuesComputational ResourcesRestricted EstimatesNotationOne-Way Fixed-Effects ModelTwo-Way Fixed-Effects ModelBalanced PanelsUnbalanced PanelsFirst-Differenced Methods for One-Way and Two-Way ModelsBetween EstimatorsPooled EstimatorOne-Way Random-Effects ModelTwo-Way Random-Effects ModelHausman-Taylor EstimationAmemiya-MaCurdy EstimationParks Method (Autoregressive Model)Da Silva Method (Variance-Component Moving Average Model)Dynamic Panel EstimatorsLinear Hypothesis TestingHeteroscedasticity-Corrected Covariance MatricesHeteroscedasticity- and Autocorrelation-Consistent Covariance MatricesR-SquareSpecification TestsPanel Data Poolability TestPanel Data Cross-Sectional Dependence TestPanel Data Unit Root TestsLagrange Multiplier (LM) Tests for Cross-Sectional and Time EffectsTests for Serial Correlation and Cross-Sectional EffectsTroubleshootingCreating ODS GraphicsOUTPUT OUT= Data SetOUTEST= Data SetOUTTRANS= Data SetPrinted OutputODS Table Names -
Examples

- References
Hausman-Taylor Estimation
The Hausman and Taylor (1981) model is a hybrid that combines the consistency of a fixed-effects model with the efficiency and applicability of a random-effects model. One-way random-effects models assume exogeneity of the regressors, namely that they be independent of both the cross-sectional and observation-level errors. In cases where some regressors are correlated with the cross-sectional errors, the random effects model can be adjusted to deal with the endogeneity.
Consider the one-way model:
![\[ y_{it}= \Strong{X}_{1it} \bbeta _1 + \Strong{X}_{2it} \bbeta _2 + \Strong{Z}_{1i} \bgamma _1 + \Strong{Z}_{2i} \bgamma _2 + \nu _ i + \epsilon _{it} \hspace{0.2 in} \]](images/etsug_panel0297.png)
The regressors are subdivided so that the 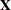 variables vary within cross sections whereas the
variables vary within cross sections whereas the 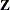 variables do not and would otherwise be dropped from a fixed-effects model. The subscript 1 denotes variables that are independent
of both error terms (exogenous variables), and the subscript 2 denotes variables that are independent of the observation-level
errors
variables do not and would otherwise be dropped from a fixed-effects model. The subscript 1 denotes variables that are independent
of both error terms (exogenous variables), and the subscript 2 denotes variables that are independent of the observation-level
errors 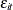 but correlated with cross-sectional errors
but correlated with cross-sectional errors 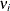 (endogenous variables). The intercept term (if your model has one) is included as part of
(endogenous variables). The intercept term (if your model has one) is included as part of 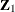 in what follows.
in what follows.
The Hausman-Taylor estimator is an instrumental variables regression on data that are weighted similarly to data for random-effects estimation. In both cases, the weights are functions of the estimated variance components.
Begin with 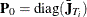 and
and 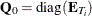 . The mean transformation vector is
. The mean transformation vector is 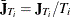 and the deviations from the mean transform is
and the deviations from the mean transform is 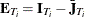 , where
, where 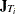 is a square matrix of ones of dimension
is a square matrix of ones of dimension 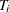 .
.
The observation-level variance is estimated from a standard fixed-effects model fit. For 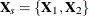 ,
, 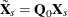 , and
, and 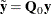 , let
, let
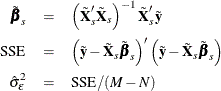
To estimate the cross-sectional error variance, form the mean residuals 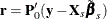 . You can use the mean residuals to obtain intermediate estimates of the coefficients for
. You can use the mean residuals to obtain intermediate estimates of the coefficients for 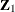 and
and 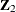 via two-stage least squares (2SLS) estimation. At the first stage, use
via two-stage least squares (2SLS) estimation. At the first stage, use 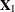 and
and 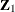 as instrumental variables to predict
as instrumental variables to predict 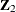 . At the second stage, regress
. At the second stage, regress  on both
on both 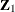 and the predicted
and the predicted 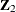 to obtain
to obtain 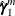 and
and 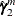 .
.
To estimate the cross-sectional variance, form 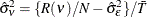 , with
, with 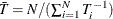 and
and
![\[ R(\nu ) = \left(\Strong{r} - \Strong{Z}_1 \hat\bgamma ^ m_1 - \Strong{Z}_2 \hat\bgamma ^ m_2 \right)’ \left(\Strong{r} - \Strong{Z}_1 \hat\bgamma ^ m_1 - \Strong{Z}_2 \hat\bgamma ^ m_2 \right) \\ \]](images/etsug_panel0317.png)
After variance-component estimation, transform the dependent variable into partial deviations: 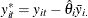 . Likewise, transform the regressors to form
. Likewise, transform the regressors to form 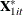 ,
, 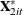 ,
, 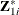 , and
, and 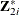 . The partial weights
. The partial weights 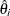 are determined by
are determined by 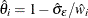 , with
, with 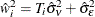 .
.
Finally, you obtain the Hausman-Taylor estimates by performing 2SLS regression of 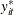 on
on 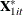 ,
, 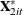 ,
, 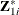 , and
, and 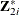 . For the first-stage regression, use the following instruments:
. For the first-stage regression, use the following instruments:
-
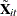 , the deviations from cross-sectional means for all time-varying variables
, the deviations from cross-sectional means for all time-varying variables 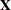 , for the ith cross section during time period t
, for the ith cross section during time period t
-
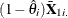 , where
, where 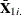 are the means of the time-varying exogenous variables for the ith cross section
are the means of the time-varying exogenous variables for the ith cross section
-
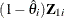
Multiplication by the factor 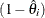 is redundant in balanced data, but necessary in the unbalanced case to produce accurate instrumentation; see Gardner (1998).
is redundant in balanced data, but necessary in the unbalanced case to produce accurate instrumentation; see Gardner (1998).
Let 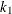 equal the number of regressors in
equal the number of regressors in 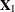 , and
, and 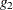 equal the number of regressors in
equal the number of regressors in 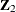 . Then the Hausman-Taylor model is identified only if
. Then the Hausman-Taylor model is identified only if 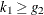 ; otherwise, no estimation will take place.
; otherwise, no estimation will take place.
Hausman and Taylor (1981) describe a specification test that compares their model to fixed effects. For a null hypothesis of fixed effects, Hausman’s
m statistic is calculated by comparing the parameter estimates and variance matrices for both models, identically to how it
is calculated for one-way random effects models; for more information, see the section Specification Tests. The degrees of freedom of the test, however, are not based on matrix rank but instead are equal to 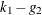 .
.