Predictive margins and average marginal effects

Contents:

Purpose / History / Requirements / Usage / Details / Limitations / Missing Values / See Also

PURPOSE:

The Margins macro fits the specified generalized linear or GEE model and estimates predictive margins and/or average marginal effects for variables in the model. Differences and contrasts of predictive margins and average marginal effects with confidence limits are also available. Margins and effects can be estimated at specified values of other model variables or at computed values such as means or medians.

HISTORY:

The version of the Margins macro that you are using is displayed when you specify anything as the first macro argument. For example:

    %margins(v)

The Margins macro always attempts to check for a later version of itself. If it is unable to do this (such as if there is no active internet connection available), the macro will issue the following message:

   NOTE: Unable to check for newer version of Margins macro.

The computations performed by the macro are not affected by the appearance of this message. However, this check can be avoided by specifying nochk as the first macro argument. This can be useful if your machine has no connection to the internet.

Version	Update Notes
2.02	In options=, added nonobs.
2.0	Removed SAS/IML® requirement. Added diff= and classgref=. In options=, added rate, nogencheck, and covout. nochk can be specified as the first (version) parameter. Removed freq= (see weight=).
1.08	Fixed bug causing errors from within= option.
1.07	Fixed bugs: mislabeled estimates, errors, or bad margin estimate if level does not exist or is dropped due to all responses missing.
1.06	Fixed problem with truncated parameter names.
1.05	Fixed problems with formatted CLASS variables.
1.03	Add within=.
1.02	Provide estimates and tests for each row in contrasts.
1.01	Allow effect= variable to be in other options.
1.0	Initial coding

REQUIREMENTS:

SAS/STAT^®

USAGE:

Follow the instructions on the Downloads tab of this sample to save the Margins macro definition. Replace the text within quotation marks in the following statement with the location of the Margins macro definition file on your system. In your SAS^® program or in the SAS editor window, specify this statement to define the Margins macro and make it available for use:

   %inc "<location of your file containing the Margins macro>";

Following this statement, you can call the Margins macro.

The Margins macro both fits the model and estimates the requested predictive margins and/or marginal effects. The macro cannot be used to compute margins or marginal effects for previously fitted models unless the data are available and the model can be specified in the macro to be refitted.

To estimate predictive margins for the levels of a variable (or combinations of levels of multiple variables) in the model, specify the options needed to fit the desired model and specify the variable(s) in margins=. To estimate the marginal effect of a continuous variable in the model, specify the options needed to fit the desired model and specify the variable in effect=.

See the Results tab for examples.

The following parameters are required when using the Margins macro.

data=data-set-name

Specify the name of the input data set to model.

response=variable

Specify the name of the response variable to be modeled. The specified variable must be numeric. Events/trials syntax for aggregated data is not supported.

model=model-effects

Specify the model to be fit by PROC GENMOD. This is the list of model effects that would appear following the equal sign (=) in the MODEL statement of PROC GENMOD. Nested effects are not supported. The fitted model is saved in an item store named _Fit. This item store can be used in the RESTORE= option in PROC PLM to do further estimation or plotting using the specified model.

The following parameters are optional. Typically, margins= or effect= (or both) are specified. If margin= and effect= are both omitted, the overall margin(s) is estimated.

margins=variable(s)

Margins are estimated for all levels or combinations of levels of the specified variable(s) in the data= data set or, if specified, in the margindata= data set. Margins are not provided for each of multiple variables separately, but this can be done as shown in Example 8 in the Results tab. The specified variable(s) must be in the data=data set and must also be specified in model=. The levels or combinations of levels defining the margins can be reduced using the margindata= data set or margwhere=. If margin= and effect= are both omitted, the overall margin is estimated, optionally with variables fixed by at=, if specified, or computed only over a subset of observations if within= is specified. See Details below.

effect=variable

Average marginal effects are estimated for the specified continuous variable. Only one variable can be specified and it must not be specified in class= or offset=. Marginal effects for multiple variables can be estimated as shown in Example 8 in the Results tab. If margins= and/or at= are also specified, the average marginal effects for the variable are estimated within each combination of levels of the margins= and/or at= variables. Marginal effects for categorical variables can be obtained as differences of predictive margins. Specify the class= variable in margins= instead of effect= and request differences with diff=.

margindata=data-set-name

Specify a data set containing the margins= variables for defining the margins to be computed. If not specified, the data= data set is used. The levels or combinations of levels defining the margins can be reduced using the margwhere= option. See Details below.

margwhere=where-condition

The specified where-condition subsets the data= or margindata= data set before determining the levels or combination of levels of the margins= variables for which predictive margins will be computed. See Details below.

roptions=response-variable-options

Specify any options for the response variable as described in the MODEL statement of PROC GENMOD. For the available response variable options, see the GENMOD documentation (SAS Note 22930).

class=variable(s)

Specify a list of any categorical predictors to be placed in a CLASS statement. Individual variable options (such as REF=) are not supported.

classgref=FIRST|LAST

For all variables in class=, specifies whether the reference levels are the first or last levels in their sorted order. Default: LAST.

dist=distribution-name

Specify the response distribution. Valid distribution names are Normal, Binomial, Poisson, Negbin (for negative binomial), Gamma, Geometric, IGaussian (for inverse Gaussian), or Tweedie. Default: Normal.

link=link-function-name

Specify the link function. Valid link function names are Identity, Log, Logit, Probit, CLL, or Power(p), where p is a numeric power value. The default link function is the canonical link for the specified distribution as shown in the description of the DIST= option in the GENMOD documentation (SAS Note 22930).

offset=variable

Specify the offset variable if needed. Typically used for Poisson or negative binomial models when modeling a rate, in which case the offset variable should be the log of the rate denominator. See options=rate. This variable should not be specified in class=, model=, margins=, at=, or effect=.

modelopts=model-options

Specify any options to appear in the PROC GENMOD MODEL statement other than DIST=, LINK=, OFFSET=, or SINGULAR=.

at=variable(s)

The margins requested in margins= or marginal effects requested in effect= will be estimated at each level or combination of levels of the specified variable(s) in the data= data set or, if specified, the atdata= data set. The specified variable(s) must be in the data= data set and must also be specified in model=. The levels or combinations of levels at which margins or effects will be computed can be reduced using the atdata= data set or atwhere=. See Details below.

atdata=data-set-name

Specify a data set containing the at= variables at which the requested margins or marginal effects will be computed. If not specified, the data= data set is used. The levels or combinations of levels at which margins or effects will be computed can be reduced using the atwhere= option. See Details below.

atwhere=where-condition

The specified where-condition subsets the data= or atdata= data set before determining the levels or combination of levels of the at= variables at which predictive margins or marginal effects will be computed. The where-condition can involve variables not in the model. See also within=. See Details below.

within=where-condition

After fitting the model, margins and marginal effects are computed by averaging only over the observations meeting the specified condition. The where-condition can involve variables not in model=. If quotation marks appear in the where-condition, use single quotation marks ('), not double quotation marks ("). Unlike margins= and at=, within= does not fix any variables in the model. It also does not affect the model fit, which is always fit on the complete data= data set (minus observations with missing values - see Missing Values below). Any statistics options (options=atmeans, mean=, and others) used to fix variables are also computed on the complete data= data set. See Details below.

diff=ALL|SEQ|number

Estimate and test differences among margins and/or marginal effects. If diff=all, then all pairwise differences are computed. Sequential differences (1-2, 2-3, 3-4, ...) are requested by diff=seq. All differences with a control are computed by diff=number, where number is the index number of the margin or marginal effect considered to be the control. If at= is specified, differencing among margins is done within each unique combination of the at= variable levels. For marginal effects, differencing is done within each unique combination of the combined margins= and at= variable levels. For differencing across the combinations, use contrasts= or specify the at= variables in margins= rather than in at= and specify diff=. See options=reverse.

contrasts=data-set-name

Specify a data set containing labels and contrast coefficients defining contrasts of predictive margins and/or average marginal effects to be estimated and tested. Note that coefficients should be given for all estimates, not just those within a combination of at= variable values. The data set must contain two character variables, LABEL and F. Each observation of the data set defines one contrast, which can be a multi-row contrast. LABEL contains the labels that will identify the contrasts in the results. F contains the coefficients defining each contrast. If the contrast has multiple rows, use commas to separate the sets of coefficients in the rows. In each row there should be as many coefficients as there are margins (or marginal effects) across any at= levels using their order as presented by the macro.

geesubject=variable or model-effect

Specifies the effect that defines correlated clusters of observations in GEE models when fitting the model in PROC GENMOD. Required when fitting a GEE model. See the description of the SUBJECT= option in the REPEATED statement in the GENMOD documentation (SAS Note 22930).

geewithin=variable

Optionally specifies the order of measurements within correlated clusters of observations in GEE models when fitting the model in PROC GENMOD. See the description of the WITHIN= option in the REPEATED statement in the GENMOD documentation (SAS Note 22930).

geecorr=structure-name

Specifies the correlation structure when fitting a GEE model in PROC GENMOD. For valid structure names, see the description of the TYPE= option in the REPEATED statement in the GENMOD documentation (SAS Note 22930). Default: IND (the independence structure).

weight=variable

Specifies a weight variable used when fitting the model in PROC GENMOD. See the description of the WEIGHT statement in the GENMOD documentation (SAS Note 22930). Noninteger values are not truncated. Weights affect the estimation of the model parameters used in the computation of predictive margins and average marginal effects. Note that because weights are not frequencies, they do not affect sample size. Consequently, weights are used in the computation of weighted statistics specified in mean=, median=, q1=, and q3= for continuous predictors, but are not used in frequencies (proportions) computed for categorical (class=) variables specified in mean= or balanced=. For aggregated data with the frequencies variable, f, the results obtained specifying weight=f is the same as the results on the equivalent disaggregated, individual level data without weight= as long as no categorical variables are specified in mean= or balanced=. If categorical variables are specified in mean= and proportions equivalent to disaggregated data are desired, then use a DATA step to create the equivalent disaggregated data and use the resulting data set in data= and omit weight=.

mean=variable(s)
median=variable(s)
q1=variable(s)
q3=variable(s)

Use these statistic options to fix model variables at computed values when estimating margins or marginal effects. The specified variables should not appear in margins= or at= but must appear in model=. Only numeric variables not specified in class= should appear in median=, q1=, or q3=. Variables in mean= can be specified in class= or not. For a class= variable specified in mean=, the observed proportions are used as values of the dummy variables that represent the variable in the model. Weighted statistics are computed for specified continuous variables when weight= is specified. However, proportions computed for categorical variables specified in mean= are not affected by weights. See weight=.

balanced=variable(s)

The specified variables must also be specified in model= and class= and not in margins= or at=. For a specified variable with k levels, the values of the dummy variables representing it in the model are all fixed at 1/k when computing predictive margins. This is not modified by weight= if specified. See weight=.

alpha=value

Specify the alpha level for confidence intervals with confidence level 1-alpha. Value must be between 0 and 1. Default: 0.05.

singular=value

Specify a singularity criterion for use in PROC GENMOD. Value must be between 0 and 1. See the description of the SINGULAR= option in the MODEL statement in the GENMOD documentation (SAS Note 22930).

options=list-of-options

Specify desired options separated by spaces. Valid options are:

atmeans

Compute predictive margins at the means of all other model variables except for those specified in at=. For marginal effects, all variables other than those in margins= or at= are fixed at their means. The mean=, median=, q1=, q3=, and balanced= options are ignored. For a class= variable, its overall observed proportions are used as values for the dummy variables that represent the variable in the model. If a weight= variable is specified, weighted means are computed for continuous variables. But for a categorical (class=) variable, weights do not contribute to observed proportions. See weight=.

cl

Provide confidence intervals for predictive margins, average marginal effects, and differences.

reverse

Reverse the direction of margin and effect differences. Ignored unless diff= is specified.

rate

After fitting the model and before computing predicted values, the offset specified in offset= is ignored by setting it equal to zero in all observations. For count models, this results in estimating rate margins rather than count margins.

covout

Saves the covariance matrix of margins (and marginal effects) in separate data sets as well as in the _Margins (and _MEffect) data sets. See Output data sets below. This is useful when using the NLMeans macro, NLEST macro, or doing other processing after completion.

desc

Adds the DESCENDING option in the PROC GENMOD statement to model the higher response level in binomial models. However, it is better to explicitly specify the response level to model using the EVENT= response variable option. For example, to model the probability that the response=1, specify roptions=event="1".

nomodel

Do not display the fitted model.

nonobs

Do not display the table showing numbers of observations read and used.

noprint

Suppress all displayed results. Note that results are always saved in data sets as shown in the Notes section below.

noprintbyat

Does not display predictive margins, average marginal effects, and differences in separate tables defined by the at= variables as is done by default. Instead, all margins are displayed in one table (similarly for marginal effects and differences) and the at= variable values are included in the table.

nogencheck

If specified, failure of the model to converge (such as when MAXITER=0 is used in modelopts=) does not halt macro execution.

DETAILS:

Predictive margins are estimates of the response mean and are typically used when fixing some, but not all, predictors in the model at specified values. The marginal effect of a continuous predictor at an observation estimates the slope of the mean response curve at that observation's setting of the predictors. It is computed as the partial derivative of the mean with respect to the predictor. As such, it is the instantaneous rate of change of the response mean at that point. The average of the marginal effects over the observations (AME) is often used as a measure of the effect of the continuous predictor on the response mean. A similar measure is the marginal effect estimated at the mean of the other predictors (MEM). For small samples, the AME is considered the better measure. A measure of the effect of a categorical predictor on the response mean can similarly be obtained as the difference in predictive margins at two of its levels. This is often considered the "marginal effect" of a binary categorical predictor.

The Margins macro estimates and tests predictive margins and marginal effects (AMEs and MEMs). Estimates and tests of differences of predictive margins and marginal effects are available with diff=, which can provide all pairwise differences, sequential differences, or differences with a specified control level. Tests of contrasts of predictive margins and marginal effects are available with contrasts=.

Note that when all model predictors are fixed at specified values, the predictive margin equals the conditional predicted mean at that setting of the predictors. The MEM, with predictors fixed at their means, is an example of this. In this case the margin can be estimated in various ways such as with the PRED= option in the OUTPUT statement of the modeling procedure, or by using the appropriate coefficients in an ESTIMATE statement with the ILINK option. When the data are balanced and the margins= variable is not involved in interactions with other predictors, the predictive margin can also be obtained with the LSMEANS statement by including the ILINK option and possibly the AT and OM options. Also in this case, the marginal effect of a categorical predictor, computed as the difference in means, can be obtained using the NLMeans macro (SAS Note 62362). However, when at least one predictor is not fixed, the Margins macro is needed to compute predictive margins.

By default, a complete replicate of the data= data set is created for each combination of levels of the margins= and/or at= variables in the data= data set. Each replicate fixes the margins= and/or at= variables for all observations at one combination of levels. The predictive margin for each combination is computed as the average predicted value in that combination's replicate. Similarly, the average marginal effect is the average of the marginal effects computed for the observations in that combination's replicate. If within= is specified, the averaging is done only over the observations that meet the specified condition. The data set containing all replicates can become very large if the input data set is large, or if there is a large number of combinations, or both. Consequently, specifying a variable in margins= or at= that has a large number of levels is not recommended unless the number of levels is constrained using one or more of margindata=, margwhere=, atdata=, and atwhere=.

Note that the distinction between specifying some variables in at= as compared to adding them to the variable(s) in margin= is generally minimal, only amounting to a difference in the way the estimates are presented in the displayed results. The same is true if the margins= variables were instead added in the at= list. That is because data replicates for the same combinations of variable levels are created in these cases. However, this will not be true if some of the combinations do not actually occur in the data. In that case, using both margins= and at= can result in additional estimates that do not appear using only margins= or only at=.

You can use the margindata= and/or atdata= option to specify the levels for or at which predictive margins (and marginal effects, if requested) will be computed. This is particularly useful when one or more desired levels does not occur in the data= data set. The margwhere= and/or atwhere= option can be used to subset the data= data set (or the corresponding margindata= or atdata= data set, if specified) before determining the levels.

Note that if neither margins= nor at= are specified, then no replication of the data= data set is done and the overall predictive margin or marginal effect is computed only using the data= data set. When margins= is not specified, the predictive margins are labeled as "Overall" margins.

In addition to fixing the values of any margins= or at= variables as described above, other predictors can be fixed at computed values using the statistics options (mean=, median=, q1=, and q3=) or balanced= or options=atmeans. Variables affected by these options are fixed at the computed statistic value in all observations in all replicates. When options=atmeans is specified, all other predictors are fixed at their means. Note that only mean= and balanced= can be used with variables specified in class=.

The delta method is used to determine the standard errors for predictive margins and marginal effects. If options=cl is specified, large-sample (Wald) tests and confidence intervals are provided.

BY group processing

While the Margins macro does not directly support BY group processing, this capability can be provided by the RunBY macro, which can run the Margins macro repeatedly for each of the BY groups in your data. See the RunBY macro documentation (SAS Note 66249) for details about its use. Also see the example titled "BY group processing" on the Results tab above.

Output data sets

The following data sets containing results are available after successful completion of the macro:

If margins= is specified:

_Margins

contains the estimated margins and their covariance matrix, standard errors, tests, and confidence intervals if requested.

_CovMarg (if options=covout is specified)

contains the estimated covariance matrix of the margins.

_DiffsPM (if diff= is specified)

contains estimates and tests of differences of the predictive margins with standard errors and confidence intervals.

_ContrastsPM (if contrasts= is specified)

contains estimates and tests of the specified contrasts of predictive margins with standard errors and confidence intervals.

If effect= is specified:

_MEffect

contains the estimated average marginal effects and their covariance matrix, standard errors, tests, and confidence intervals if requested.

_CovMeff (if options=covout is specified)

contains the estimated covariance matrix of the average marginal effects.

_DiffsME (if diff= is specified)

contains estimates and tests of differences of the average marginal effects with standard errors and confidence intervals

_ContrastME (if contrasts= is specified)

contains estimates and tests of the specified contrasts of average marginal effects with standard errors and confidence intervals.

LIMITATIONS and ERRORS:

If the macro terminates with an error listing valid values of options= when the specified options are correct or when options= was not specified, then download and use version 2.02 (or later) as discussed in the Usage section above.

 

The Margins macro can be used only with a subset of the models available in PROC GENMOD since that procedure is used to fit the specified model. It cannot be used with multinomial or zero-inflated models available in GENMOD. Models for survey data, or for survival data, or models containing random effects or effects constructed by the EFFECT statement are likewise exempted.

Events/trials syntax, as used in several procedures, is not supported for the analysis of aggregated binomial data. Instead, modify the data so that each events/trials observation becomes two observations with a variable indicating the response level and a variable containing the observed count for that response level. Then specify the first variable in response= and the count variable in weight=.

MISSING VALUES:

Observations with missing values in any of the model variables are omitted from the analysis. However, observations that are missing only on the response are used. Note that predicted values can be computed for observations missing only on the response and therefore they contribute in the computation of predictive margins and marginal effects. When any of mean=, median=, q1=, q3=, balanced=, or options=atmeans is specified, these observations also contribute to the computed statistics.

SEE ALSO:

The NLEST macro (SAS Note 58775) estimates and tests linear or nonlinear combinations of model parameters and can be used to estimate predictive margins when all predictors are fixed. It can also be used following the Margins macro to estimate and test functions of the margins or marginal effects not possible in the Margins macro such as relative risks or odds ratios of margins. To do this, specify options=covout in the Margins macro and then specify the _Margins or _MEffect data set in inest= and the _CovMarg or _CovMeff data set in incovb= in the NLEST macro. See the example in the Results tab.

The NLMeans macro (SAS Note 62362) can perform multiple comparisons among the levels of a model effect on the mean scale. It can be used to estimate differences of predictive margins when all predictors are fixed.

Estimates of marginal effects at the observation level are also available in the QLIM procedure in SAS/ETS^® for the models that procedure fits. Use the MARGINAL option in the OUTPUT statement of PROC QLIM. Standard errors for observation marginal effects are not available. As of SAS^® 9.4M6 (TS1M6), marginal effects computed in PROC QLIM are valid only for predictors that are not involved in higher-order model effects such as interactions.

---

These sample files and code examples are provided by SAS Institute Inc. "as is" without warranty of any kind, either express or implied, including but not limited to the implied warranties of merchantability and fitness for a particular purpose. Recipients acknowledge and agree that SAS Institute shall not be liable for any damages whatsoever arising out of their use of this material. In addition, SAS Institute will provide no support for the materials contained herein.

---

---

These sample files and code examples are provided by SAS Institute Inc. "as is" without warranty of any kind, either express or implied, including but not limited to the implied warranties of merchantability and fitness for a particular purpose. Recipients acknowledge and agree that SAS Institute shall not be liable for any damages whatsoever arising out of their use of this material. In addition, SAS Institute will provide no support for the materials contained herein.

In addition to the following example, several more examples of using the Margins macro can be found in these notes:

• Marginal effect estimation for predictors in logistic and probit models (SAS Note 22604)
• Estimating differences in probabilities (marginal effects) with confidence interval (SAS Note 37228)
• Estimating the difference in differences of means (SAS Note 61830)
• Estimating the risk (proportion) difference for matched pairs data with binary response (SAS Note 46997)
• Estimate and plot the effect of changing a continuous predictor in a spline (SAS Note 67024)
• Odds ratio, risk difference, marginal effect for logistic model with polynomial or spline (SAS Note 35189)
• Compare group slopes on a continuous predictor in a spline or polynomial effect (SAS Note 70756)
• Comparing parameters (slopes) from a model fit to two or more groups (SAS Note 24177)

EXAMPLE 1: Predictive margins in a binary logistic model

The following statements estimate and test predictive margins for the Neuralgia data set presented in the example titled "Logistic Modeling with Categorical Predictors" in the LOGISTIC documentation (SAS Note 22930). Treatment predictive margins are computed for males and females. Since the Margins macro requires a numeric response variable, the NoPain variable is created with value 1 when Pain='No' and 0 otherwise. The probability of no pain is modeled as a result of roptions=event='1'. Confidence intervals are requested by options=cl.

data Neur; 
  set Neuralgia; 
  NoPain=(pain='No'); 
  run;
%Margins(data     = Neur,
         class    = Treatment Sex,
         response = NoPain,
         roptions = event='1',
         dist     = binomial,
         model    = Treatment Sex Treatment*Sex Age Duration,
         margins  = Treatment, 
         at       = Sex,
         options  = cl)

The predictive margins are presented in the following tables. For example, the estimated probability of no pain for females in Treatment A is 0.82, and 0.62 for males. Notice that Treatment P produces a noticeably smaller probability than Treatments A or B, and females have higher probabilities in all Treatments.

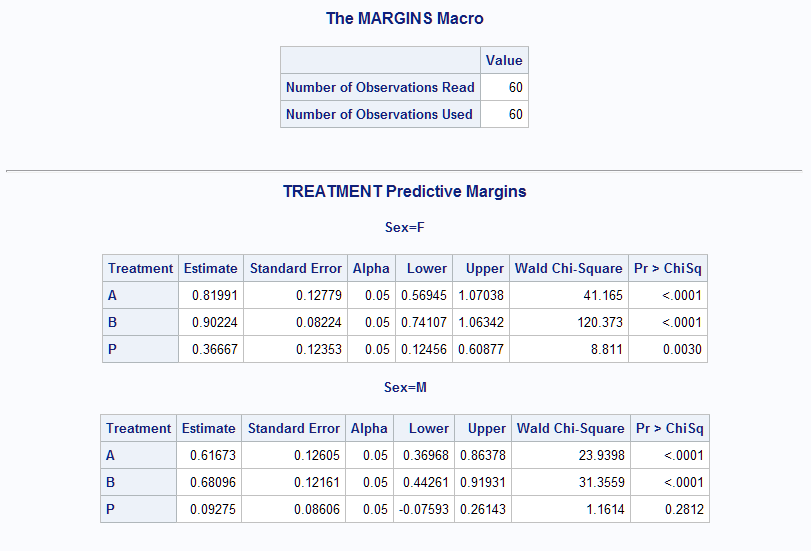
Adding the atmeans option fixes all other predictors in the model at their mean values. With this option, all predictors in the model are fixed either by margins= or atmeans. The nomodel option prevents displaying the fitted model again.

%Margins(data     = Neur,
         class    = Treatment Sex,
         response = NoPain,
         roptions = event='1',
         dist     = binomial,
         model    = Treatment Sex Treatment*Sex Age Duration,
         margins  = Treatment, 
         at       = Sex,
         options  = cl nomodel atmeans)

Following are the predictive margins at the means of Age and Duration. The mean values are shown preceding the margins table. The margins at the means are roughly similar to the previous values.

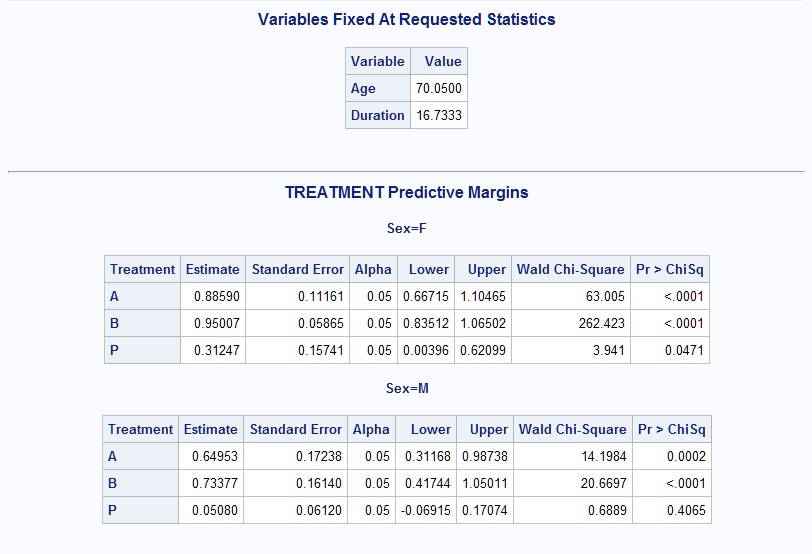
In the analysis with options=atmeans, all predictors are fixed. In this case, the same results can be obtained using the LSMEANS statement in PROC LOGISTIC as shown below.

proc logistic data=Neur;
  class Treatment Sex / param=glm;
  model NoPain(event='1') = Treatment Sex Treatment*Sex Age Duration;
  lsmeans Treatment*Sex / ilink cl at means;
  run;

The Mean column displays the predictive margins, which match those in the previous analysis from the Margins macro.

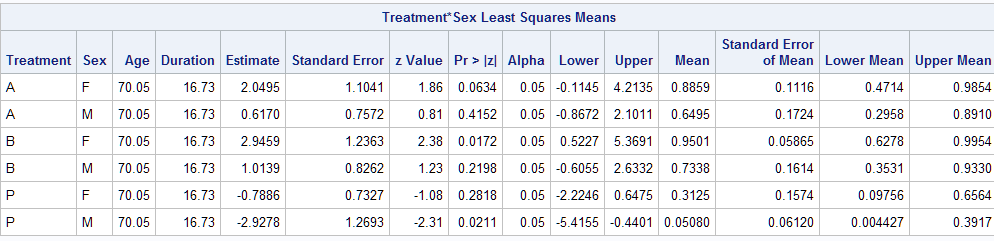
Differences among the treatment predictive margins, computed within the sexes, can be estimated and tested by adding diff=all. This can be done with or without fixing the other model predictors at their means with the atmeans option.

%Margins(data     = Neur,
         class    = Treatment Sex,
         response = NoPain,
         roptions = event='1',
         dist     = binomial,
         model    = Treatment Sex Treatment*Sex Age Duration,
         margins  = Treatment, 
         at       = Sex,
         diff     = all,
         options  = cl nomodel)

The results show that both the A and B Treatments produce significantly higher probability than Treatment P, in both sexes. Treatments A and B do not differ significantly.

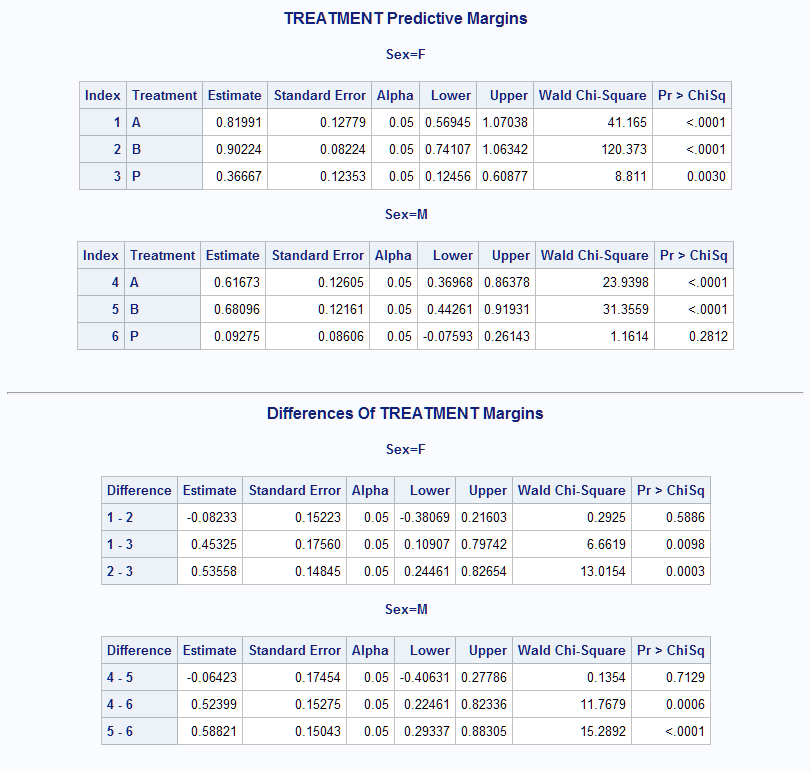
EXAMPLE 2: Marginal effects in a binary logistic model

Using the same data as the previous example, the following estimates the marginal effect for Sex at the means of Treatment, Age and Duration. Since Sex is a binary CLASS variable, its marginal effect is computed as the difference in predictive margins. Since Treatment is also a CLASS variable, its mean is represented in the model by using the overall observed proportions of the Treatments in its dummy variables.

%Margins(data     = Neur,
         class    = Treatment Sex,
         response = NoPain,
         roptions = event='1',
         dist     = binomial,
         model    = Treatment Sex Treatment*Sex Age Duration,
         margins  = Sex,
         diff     = all,
         options  = cl nomodel atmeans)

The Treatment, Age, and Duration means used in the computations are shown first. Since the Treatments appear equally in the data, the proportions are balanced in the same way as if balanced=Treatment had been specified. Next are the predictive margins for Sex, followed by the marginal effect for Sex, computed as the difference in predictive margins. The marginal effect of Sex, 0.41, is significant (p=0.0095) indicating that the probability for Females is significantly larger than for Males. Note that the direction of the difference is indicated by the index values shown in the Difference column ("1-2"). If the Male-Female difference is desired, specify options=reverse.

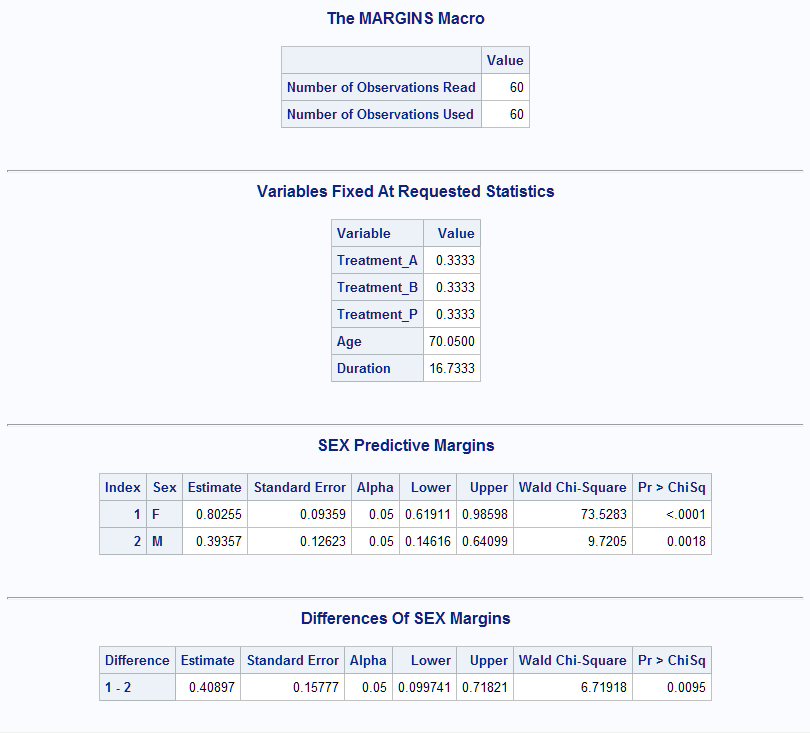
The following estimates the average marginal effect of the continuous predictor, Age. The model is expanded to allow for the Age effect to vary with Treatment by including the Age*Treatment interaction. Note that the vertical bar ("|") between variables is equivalent to specifying both main effects and the interaction. The marginal effect computation uses the observed values of the predictors rather than their means since the atmeans option is omitted.

%Margins(data     = Neur,
         class    = Treatment Sex,
         response = NoPain,
         roptions = event='1',
         dist     = binomial,
         model    = Treatment|Sex Treatment|Age Duration,
         effect   = Age, 
         options  = cl nomodel)

The estimated margin, -0.036, indicates that increasing Age significantly decreases the probability (p=0.0011).

The marginal effect of Age can be compared between the Treatments by specifying a contrast. The following DATA step creates the appropriate data set. The data set must always include a LABEL variable containing labels for the contrasts, and a variable F, which contains the contrasts coefficients. Both variables must be character variables. The rows of the specified contrast request the three pairwise differences among the marginal effects for Age in the three Treatments. Estimates of the marginal effect of Age at each Treatment are requested with at=Treatment. The noprintbyat option arranges the three marginal effects in a single table instead of separate tables labeled by the Treatment.

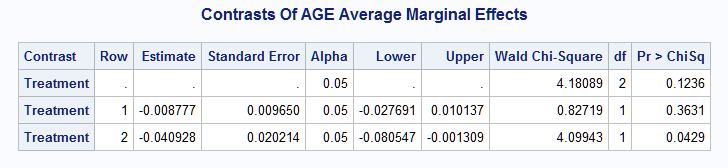
data C; 
  length label f $32767; 
  infile datalines delimiter='|';
  input label f; 
  datalines;
Treatment | 1 -1 0, 1  0 -1, 0  1 -1
;
%Margins(data     = Neur,
         class    = Treatment Sex,
         response = NoPain,
         roptions = event='1',
         dist     = binomial,
         model    = Treatment|Sex Treatment|Age Duration,
         effect   = Age,
         at       = Treatment,
         contrasts= C,
         options  = cl nomodel noprintbyat)

The three pairwise comparisons indicate that Age significantly decreases the probability of neuralgia in Treatments A and B, but not P. Further, the effect of Age differs significantly only between Treatments A and P (p=0.0429).

However, a note in the log indicates that the joint test for the contrast rows could not be provided resulting in missing statistic and p-value in the first row of the table. Because Treatment has three levels and therefore only two degrees of freedom, only two comparisons are independent. Consequently, in order to conduct the joint test, the contrast should contain only two of the three pairwise comparisons. By keeping only the first two of the three observations in data set C, the following table is produced, which provides the joint test which shows no overall difference.

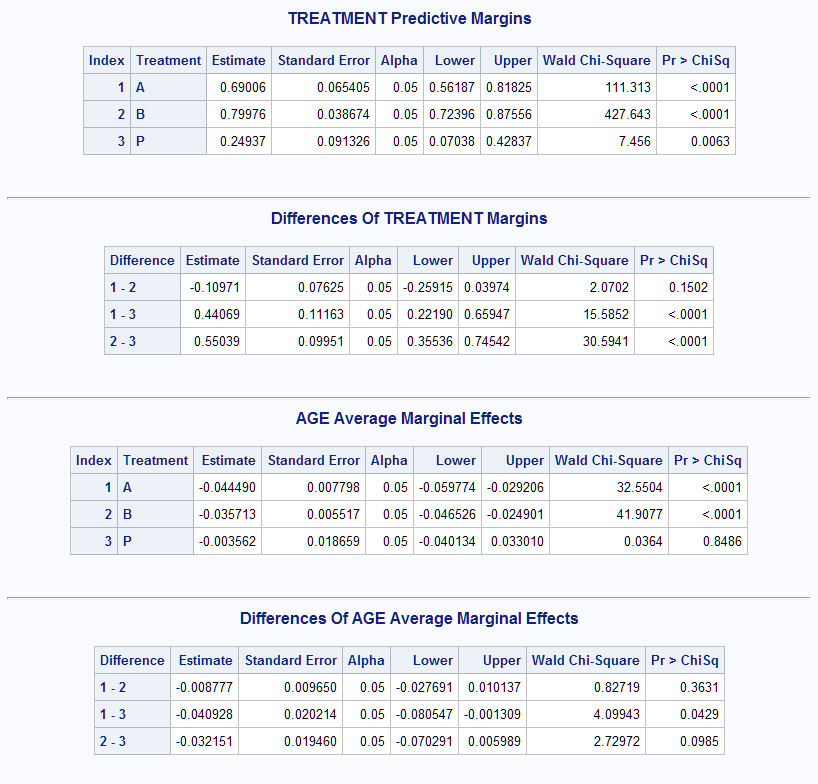
The same pairwise comparison results can be obtained without the need for contrasts= by specifying margins=Treatment and diff=all.

%Margins(data     = Neur,
         class    = Treatment Sex,
         response = NoPain,
         roptions = event='1',
         dist     = binomial,
         model    = Treatment|Sex Treatment|Age Duration,
         effect   = Age,
         margins  = Treatment,
         diff     = all,
         options  = cl nomodel)

With this approach, the Treatment predictive margins and their differences are also given.

EXAMPLE 3: Marginal effects in a Poisson model

This example uses data presented and analyzed by McCullagh and Nelder (1989). The data contain counts of the number of damage incidents (Y) occurring to individual ships over their total months of service (MONTHS). A Poisson model is used to model the incidence rate (Y/MONTHS). Predictors are the type of ship (TYPE), period of operation (PERIOD), and year of construction (YEAR). In order to model the incidence rate, the log of the months of service (LOGMONTHS) is used as an offset in the model.

The following macro call models the incidence rate and estimates and tests the marginal effect of the continuous YEAR variable on the rate. The first levels of the categorical TYPE and PERIOD predictors are specified as reference levels in the model with classgref=first. LOGMONTHS is specified as the offset. effect=year and options=rate cl together request estimation of the rate marginal effect of YEAR along with a confidence interval. If rate is not specified, the macro estimates the marginal effect of YEAR on the mean incidence count rather than the incidence rate.

%Margins(data     = ship,
         class    = type period,
         classgref= first,
         response = y, 
         offset   = logmonths,
         model    = type year period,
         dist     = poisson,
         effect   = year, 
         options  = rate cl)

The estimated marginal effect of YEAR on the incidence rate is 0.00068 and differs significantly from zero (p=0.0024).

EXAMPLE 4: Margins and marginal effects in a GEE model

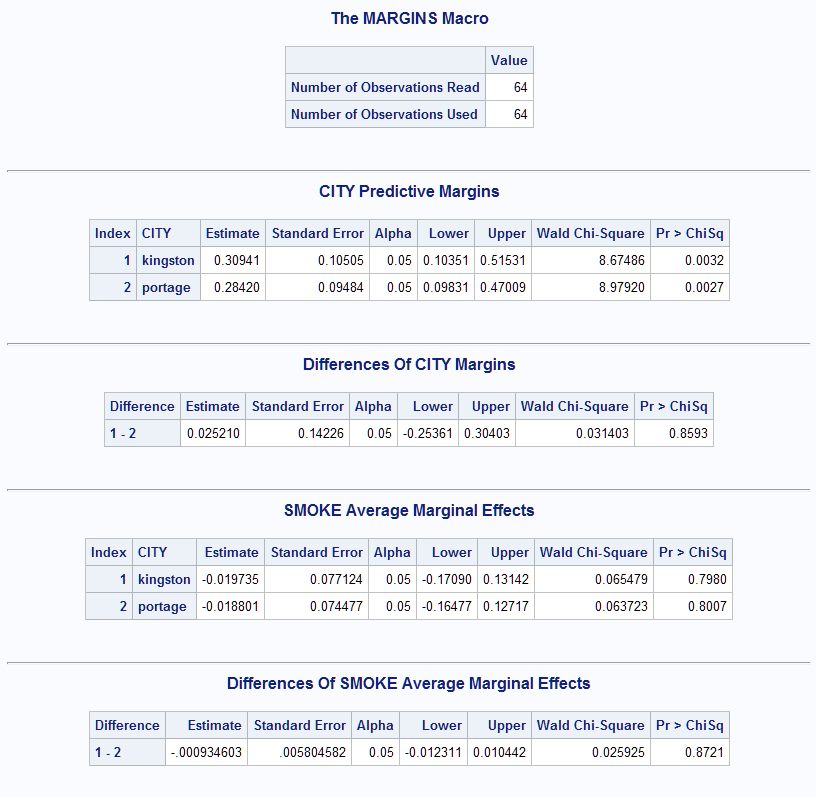
This example uses the data in the Generalized Estimating Equations (GEE) example in the Getting Started section of the GENMOD documentation (SAS Note 22930). This call of the Margins macro estimates a logistic GEE model for the probability of Wheezing. Then it estimates and tests the predictive margins for the City levels and the average marginal effect of Smoke in each City. An estimate of the marginal effect of City, computed as the difference in its predictive margins, is provided by diff=all. The difference in the Smoke marginal effects is also provided.

%Margins(data     = Six,
         class    = Case City,
         response = Wheeze, roptions = event='1',
         model    = City Age Smoke,
         dist     = binomial,
         geesubject = Case, geecorr = exch, 
         margins  = City, 
         effect   = Smoke,
         diff     = all,
         options  = cl)

The results show that the estimated probabilities of wheezing in the two cities are both near 0.3 and the difference, the marginal effect of City, is not significant (p=0.8593). The average marginal effect of Smoke is also shown to not differ significantly (p=0.8721) between the cities and, in fact, the Smoke effect on the probability of wheezing is not significant in either city.

EXAMPLE 5: Marginal effect in a log-linked gamma model

The following example appears in the NLMeans macro documentation (SAS NOte 62362) where that macro is used to estimate the difference in mean failure times for two manufacturers. This can also be considered the marginal effect of the binary manufacturer variable, MFG, and can be estimated using the Margins macro.

The following macro call estimates the marginal effect as the difference in predictive margins for MFG. The model specified by class=, response=, dist=, and model= is a log-linked gamma model. The predictive margins for the manufacturers and their difference is requested by margins= and diff=all.

%Margins(data     = lifdat,
         class    = mfg,
         response = lifetime,
         dist     = gamma,
         model    = mfg,
         margins  = mfg,
         diff     = all,
         options  = cl)

These results duplicate those from the LSMEANS statement and the NLMeans macro in the NLMeans macro documentation. Each manufacturer's mean failure time is significantly different from zero (p<0.0001). The estimated marginal effect for MFG is 9.23 and is not significant (p=0.8986).

EXAMPLE 6: Relative risk

The Margins macro can estimate differences or other linear combinations of predictive margins or marginal effects by specifying diff= or contrasts=. To estimate other functions, the NLEST macro (SAS Note 58775) can be used. The NLEST macro can estimate and test linear and nonlinear combinations of model parameters given estimates and their covariance matrix.

To do this with margins or marginal effects, specify options=covout to create a separate data set containing the covariance matrix of the margins (_CovMarg) or marginal effects (_CovMeff). Estimates of the margins or marginal effects are automatically saved in data set _Margins or _MEffect. Specify the estimates in inest= and their covariance matrix in incovb= in the NLEST macro. Then specify the desired function of those estimates in f=. In this function, the estimates are referred to using the names b_p1, b_p2, b_p3, and so on in the order presented by the macro. The result can optionally be labelled by specifying label=. Other options are available and are described in the NLEST macro documentation (SAS Note 58775).

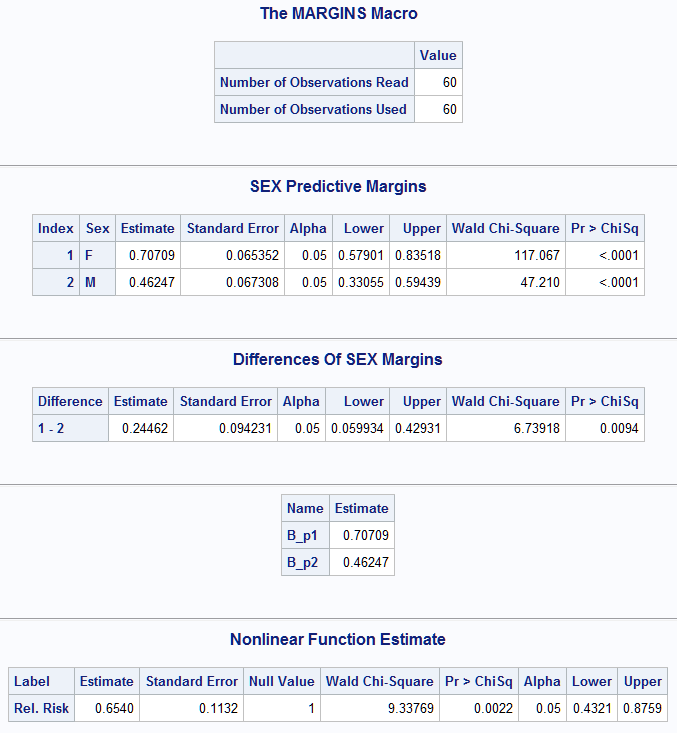
The following example estimates the relative risk of the predictive margins of Sex levels estimated using a logistic model on the binary NoPain variable. The predictive margins are estimated event probabilities. The relative risk is a ratio of these probability estimates. While the Margins macro can estimate the margins and their difference, as done below with diff=, it cannot directly estimate the ratio of margins. The following Margins macro call creates the _Margins data set containing the estimates of the margins, and options=covout creates the _CovMarg data set containing their covariance matrix. These are then specified in the NLEST macro. The function in f= specifies the ratio of the Sex='M' margin, referred to as b_p2 since it is the second estimate, to the Sex='F' margin, referred to as b_p1. To test that this ratio is equal to 1 rather than equal to 0 as is the default, null=1 is also specified. A label is specified in label=.

%Margins(data     = Neur,
         class    = Treatment Sex,
         response = NoPain,
         roptions = event='1',
         dist     = binomial,
         model    = Treatment Sex Treatment*Sex Age Duration,
         margins  = Sex, 
         diff     = all,
         options  = covout cl nomodel)
%nlest(inest=_Margins, incovb=_CovMarg, f=b_p2/b_p1, null=1, label=Rel. Risk)

The estimated Sex margins and difference are provided by the Margins macro. The NLEST macro confirms the names assigned to the margins followed by the estimated relative risk (0.6540), which differs significantly from 1 (p=0.0022). A 95% confidence interval is also provided.

EXAMPLE 7: BY group processing using RunBy

While the Margins macro does not support BY processing directly, the general purpose RunBY macro (SAS Note 66249) can be used to run the macro on BY groups in the data. The following uses the Neur data set in the examples above. In the statements below, a DATA step is used to subset the Neur data set to each BY group in turn. This is done with a WHERE statement that specifies the special macro variables, _BYx and _LVLx, which are used by the RunBY macro to process each BY group. The BYlabel macro variable is also used to label the displayed results with the BY group definition. Since the Margins macro writes its own titles, a FOOTNOTE statement is used instead of a TITLE statement to provide the label.

      %macro code();
        data subset; set Neur; where &_BY1=&_LVL1; run;
        footnote "Above for &BYlabel";
        %margins(data=subset, class=treatment, response=NoPain, roptions=event='1', 
                 dist=binomial, model=treatment age duration, margins=treatment, options=nomodel)
        footnote;
      %mend;
      %RunBY(data=Neur, by=sex)

EXAMPLE 8: Multiple margins= or effect= variables using RunBy

The Margins macro estimates margins for the levels of one variable or the combinations of levels of multiple variables. It does not estimate margins for the levels of each variable separately if multiple variables are specified in margins=. Similarly, only one variable can be specified in effect=. To estimate margins or marginal effects separately for multiple variables, you can use the general purpose RunBY macro (SAS Note 66249) to run the Margins macro repeatedly for each variable in a list.

To illustrate, the statements below run the Margins macro for each of two variables, Job and Reason, to estimate predictive margins separately for each. The DATA step creates data set MargVars with a variable named MargVar containing these two variable names. The appropriate Margins macro call is placed in the special macro, CODE, which the RunBY macro runs once for each level of the by= variable in the data= data set. By specifying data=MargVars and by=MargVar, RunBY runs the code in the CODE macro for each of the two variables. In each run, each variable name in turn is stored in the special macro variable _LVL1, so this macro variable is specified in margins=. To avoid repeatedly displaying the fitted model, options=nomodel is also specified. Since the variable name specified in margins= does not need to be quoted, lvlquote=no is specified in RunBY. To run Margins on the variables in the order specified in the MargVars data set, order=data is also included.

      data MargVars; 
        length MargVar $20;
        input MargVar $ @@;
        datalines;
        job reason
        ;
      %macro code();
        %margins(data=sampsio.hmeq, response=bad, roptions=event='1', dist=binomial,
                 class=job reason,
                 model=job reason Delinq Derog, margins=&_LVL1, 
                 options=cl nomodel)
      %mend;
      %RunBY(data=MargVars, by=MargVar, lvlquote=no, order=data)

If you want to create a data set containing all of the margins from both variables rather than have them displayed, the following variation can be used. All displayed results from the Margins macro are suppressed by options=noprint. Since the _Margins data set created by the Margins macro does not contain the name of the margins= variable, that is added by the DATA step prior to the PROC APPEND step, which accumulates the _Margins data sets into data set AllMargins. To avoid problems caused by varying numbers of levels and differing names of the variable containing the level names, the DROP= and RENAME= options are used in the APPEND step.

      %macro code();
        %margins(data=sampsio.hmeq, response=bad, roptions=event='1', dist=binomial,
                 class=job reason,
                 model=job reason Delinq Derog, margins=&_LVL1, 
                 options=cl noprint)
        data _Margins; set _Margins; length MargVar $20; MargVar="&_LVL1"; run;
        proc append base=AllMargins data=_Margins(drop=cov: rename=(&_LVL1=Level)); run;
      %mend;
      %RunBY(data=MargVars, by=MargVar, lvlquote=no, order=data)
      proc print label; id margvar level; 
        var estimate stderrpm lower upper chisq pr;
        title "Predictive Margins";
        run;

The following is the AllMargins data set displayed by PROC PRINT.

The same approaches as above can be used for multiple marginal effects variables. In this case, the DROP= and RENAME= options in the APPEND step are not necessary.

Right-click the link below and select Save to save the Margins macro definition to a file. It is recommended that you name the file margins.sas.

Download and save margins.sas

A fix for this issue for SAS/STAT 15.3 is available at:

https://tshf.sas.com/techsup/download/hotfix/HF2/L9L.html#63038

---

Estimate and test predictive margins and average marginal effects in generalized linear and GEE models, optionally at specified values of other model variables. Differences and contrasts with confidence limits are also available.

Type:	Sample
Topic:	Analytics ==> analytics SAS Reference ==> Macro

Date Modified:	2023-12-13 14:17:55
Date Created:	2018-10-08 13:34:26

Operating System and Release Information

Product Family	Product	Host	SAS Release
			Starting	Ending
SAS System	SAS/STAT	Windows 7 Professional x64
		Windows 7 Professional 32 bit
		Windows 7 Home Premium x64
		Windows 7 Home Premium 32 bit
		Windows 7 Enterprise x64
		Windows 7 Enterprise 32 bit
		Microsoft Windows Server 2016
		Microsoft Windows XP Professional
		Microsoft Windows Server 2012 Std
		Microsoft Windows Server 2012 R2 Std
		Microsoft Windows Server 2012 R2 Datacenter
		Microsoft Windows Server 2012 Datacenter
		Microsoft Windows Server 2008 for x64
		Microsoft Windows Server 2008 R2
		Microsoft Windows Server 2008
		Microsoft Windows Server 2003 for x64
		Microsoft Windows Server 2003 Standard Edition
		Microsoft Windows Server 2003 Enterprise Edition
		Microsoft Windows Server 2003 Datacenter Edition
		Microsoft Windows NT Workstation
		Microsoft Windows 2000 Professional
		Microsoft Windows 2000 Server
		Microsoft Windows 2000 Datacenter Server
		Microsoft Windows 95/98
		Microsoft Windows 2000 Advanced Server
		Microsoft Windows 10
		Microsoft Windows 8.1 Pro x64
		Microsoft Windows 8.1 Pro 32-bit
		Microsoft Windows 8.1 Enterprise x64
		Microsoft Windows 8.1 Enterprise 32-bit
		Microsoft Windows 8 Pro x64
		Microsoft Windows 8 Pro 32-bit
		Microsoft Windows 8 Enterprise x64
		OS/2
		Microsoft Windows 8 Enterprise 32-bit
		Microsoft® Windows® for x64
		Microsoft Windows XP 64-bit Edition
		Microsoft Windows Server 2003 Enterprise 64-bit Edition
		Microsoft Windows Server 2003 Datacenter 64-bit Edition
		Microsoft® Windows® for 64-Bit Itanium-based Systems
		OpenVMS VAX
		z/OS 64-bit
		z/OS
		Windows 7 Ultimate 32 bit
		Windows 7 Ultimate x64
		Windows Millennium Edition (Me)
		Windows Vista
		Windows Vista for x64
		64-bit Enabled AIX
		64-bit Enabled HP-UX
		64-bit Enabled Solaris
		ABI+ for Intel Architecture
		AIX
		HP-UX
		HP-UX IPF
		IRIX
		Linux
		Linux for x64
		Linux on Itanium
		OpenVMS Alpha
		OpenVMS on HP Integrity
		Solaris
		Solaris for x64
		Tru64 UNIX