Usage Note 61830: Estimating the difference in differences of means
 |  |  |
Intervention analysis assesses the effect of an intervention on the response in studies where the response is observed before and after the intervention. The intervention might be a treatment of some sort, such as a drug, or a change in conditions. Typically, there is a treated or exposed group of subjects who receive the intervention and an unexposed group of subjects who do not.
When only a single response measure is obtained both before and after intervention, a comparison of the changes in the mean responses from the two groups, the difference in difference, is of primary interest as a measure of the effect of the intervention. This is discussed below. Alternatively, if the study measures subjects at multiple time points both before and after the intervention, the analysis is often called interrupted time series analysis, which is discussed in SAS Note 70498.
Model for Normal Response with Independent Groups Pre- and Post-Intervention
When fitting a model that includes the interaction of two predictors, it is often of interest to estimate the difference in the differences of means. For example, for a model containing two binary predictors, A and B each with levels 1 and 0, and their interaction:
μAB = λ + αA + βB + γAB
you might want to estimate the difference in the effect of A at the two levels of B. This is the difference of the A means at level 1 of B minus the difference of the A means at level 0 of B. Here's it is in terms of the above model parameters:
(μ11 - μ01) - (μ10 - μ00) = [(λ + α + β + γ) - (λ + β)] - [(λ + α) - (λ)] = γ
You can see why this is called a "difference in differences" estimate. Note that the interaction parameter is the difference in difference estimate. But this is only the case when the model is an ordinary regression model, such as fit by PROC REG or PROC GLM, or equivalently a generalized linear model with identity link function, such as fit by PROC GENMOD or PROC GLIMMIX. For such a model, the fitting procedure directly provides the difference in differences of means estimate and a test of its significance in the Parameter Estimates table. It can also be produced using the ESTIMATE statement or the LSMESTIMATE statement. The LSMEANS statement displays the mean estimates. With the LSMESTIMATE statement, you can estimate a contrast of the means by specifying contrast coefficients using the order of the means presented by the LSMEANS statement.
The following statements generate some example data and fit a model to the normally distributed response using the identity link:
data a;
sd=3;
do a=1,0;
do b=1,0;
input mean @@;
do rep=1 to 10;
y=rannor(23425)*sd+mean;
output;
end;
end; end;
datalines;
50 70 40 40
;
proc genmod;
class a b / ref=first;
model y = a b a*b;
estimate "Diff in Diff" a*b 1 -1 -1 1;
lsmeans a*b;
lsmestimate a*b "Diff in Diff" 1 -1 -1 1;
run;
The interaction parameter and estimated difference in differences of means is about -21 and is significantly different from zero (p<0.0001). The same estimate is provided by the ESTIMATE and LSMESTIMATE statements. The means at each of the four A-B combinations are given by the LSMEANS statement. Using those values, you can see that -21 ≅ (50-40)-(69-38). A confidence interval for the difference in differences of means is (-24.3, -17.7). Adding the CL option in the LSMEANS and LSMESTIMATE statements adds confidence intervals in the results from those statements:
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Difference in Difference Analysis in a Pre/Post Longitudinal Study
Difference in difference analysis is often used for studies in which subjects are assigned randomly to exposed and control groups and the subjects in the exposed group are measured before and after some intervention, such as a drug, is applied. Subjects in the control group do not experience the intervention. In other studies, the groups differ on some demographic measure such as gender and both groups experience the intervention. In either case, it is of interest to assess the effect of the intervention in the two groups and whether that effect differs between the groups. The difference in difference estimates the difference between groups in the mean response change from pre-intervention to post-intervention.
The following statements generate data similar to what might come from a pre/post longitudinal study:
data a;
sd=3;
do Exposed=1,0;
input mean_post mean_pre @;
do ID=1 to 10;
Y_post=rannor(23425)*sd+mean_post;
Y_pre=rannor(23425)*sd+mean_pre;
output;
end;
end;
datalines;
50 70 40 40
;
The following statements rearrange the data so that the responses from each subject appear in a single variable, Y, in separate observations. The variable, POST, indicates whether the observation contains the pre- or post-intervention response. The GENMOD statements includes the REPEATED statement to fit a Generalized Estimating Equations (GEE) model to account for the correlation that exists between the responses from the same subject. The SUBJECT= effect is specified as ID(EXPOSED) rather than ID because the same ID values (1, 2, ...) are used in each group. If SUBJECT=ID were specified the two observations from ID=1 in the exposed group and the two observations from ID=1 in the unexposed group would be treated as coming from the same subject.
The group means before and after intervention and the difference in difference estimate are provided, as above, by the ESTIMATE, LSMEANS, and LSMESTIMATE statements:
data a;
keep exposed id post y;
set a;
Post=1; y=y_post; output;
Post=0; y=y_pre; output;
run;
proc genmod;
class id exposed post / ref=first;
model y = exposed post exposed*post;
repeated subject=id(exposed);
estimate "DID Post(E-U)-Pre(E-U)" exposed*post 1 -1 -1 1;
lsmeans exposed*post;
lsmestimate exposed*post "DID Post(E-U)-Pre(E-U)" 1 -1 -1 1;
run;
Generalized Linear Models with a Non-Identity Link
Suppose that instead of an ordinary regression model, you are interested in estimating the difference in differences of means (probabilities) for a binary logistic model:
LogOddsAB = λ + αA + βB + γAB
In this model, or indeed with any generalized linear model, the interaction is still a difference in differences estimate — but not of the means, but rather of the means transformed by the link function. In the case of a logistic model, it estimates the difference in differences of log odds (logits). The difference in differences of means requires that each of the four parts of the estimator be a mean rather than a log odds, and that requires applying the inverse of the link function to each of the four parts. The LOGISTIC function in SAS® is the inverse of the logit link function 1/(1+e-LogOdds):
[logistic(λ + α + β + γ) - logistic(λ + β)] - [logistic(λ + α) - logistic(λ)]
Because this is not a linear combination of the model parameters or of the LS-means, you cannot use the ESTIMATE or LSMESTIMATE statements to estimate the difference in differences of means. However, you can use them as above to estimate the difference in differences of log odds.
The following statements generate example data and fit a logistic model. The ILINK option in the LSMEANS statement below applies the inverse link function to the four individual log odds estimates, resulting in a Mean column that shows the mean (probability) estimates. The ILINK option only applies the inverse link to the entire estimate, so it cannot be used when differences (in LSMEANS) or contrasts (in LSMESTIMATE) are requested. Note that the LSMEANS and LSMESTIMATE statements require that CLASS variables use the GLM parameterization (PARAM=GLM):
data a;
do a=1,0;
do b=1,0;
input mean @@;
n=ranbin(23425,100,mean);
do rep=1 to n; y=1; output; end;
do rep=n+1 to 100; y=0; output; end;
end; end;
datalines;
.5 .7 .4 .4
;
proc logistic;
class a b / param=glm ref=first;
model y(event="1") = a b a*b;
estimate "Diff in Diff" a*b 1 -1 -1 1;
lsmeans a*b / e ilink;
ods output coef=coeffs;
lsmestimate a*b "Diff in Diff LogOdds" 1 -1 -1 1;
store log;
run;
The difference in differences estimate on the log odds scale appears as the interaction parameter estimate as well as from the ESTIMATE and LSMESTIMATE statements. The difference in differences estimate of log odds is -1.1113 ≅ [0.12-(-0.16)]-[0.95-(-0.45)]:
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
The estimator of the difference in differences of means shown above for this logistic model is a nonlinear combination of model parameters. Such an estimate can be computed using the NLMeans macro (SAS Note 62362), the NLEST macro (SAS Note 58775), or by fitting the model in PROC NLMIXED and using its ESTIMATE statement. The mean estimates are also considered predictive margins. The difference in difference is a contrast of these margins that can be estimated by the Margins macro (SAS Note 63038). In addition to using these to estimate the difference in difference of means, they can also be used to estimate pairwise differences of means as illustrated in SAS Note 37228.
Using the Margins Macro
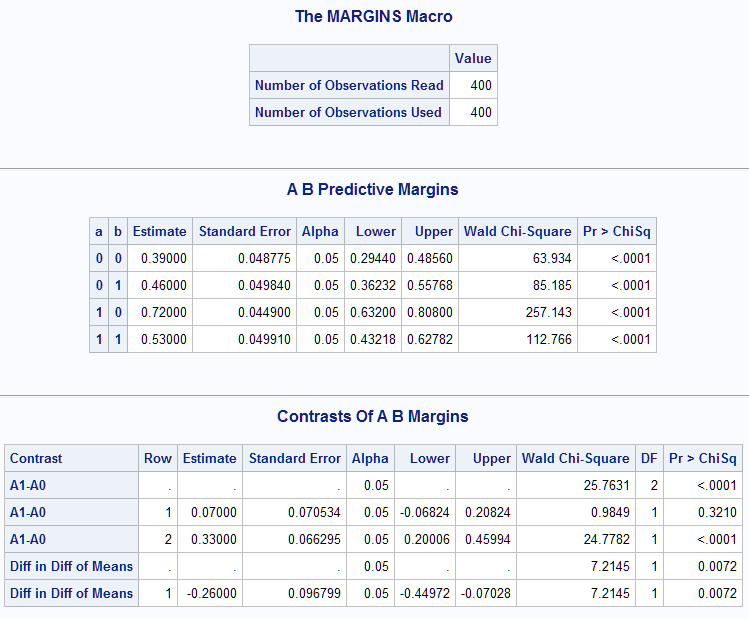
The Margins macro (SAS Note 63038) can estimate and test the predictive margins (means) of the A,B combinations. It first fits the model that you specify. In the macro call shown below, the specification of the response=, roptions=, class=, classgref=, model=, and dist= options reproduce the logistic model as done above in PROC LOGISTIC. Estimates of the A,B margins are requested by margins=a b. The macro fits the model using the standard order of the A,B combinations and displays the margins in that order: A0B0, A0B1, A1B0, A1B1. Confidence intervals for the margins and the contrast row estimates are requested by options=cl.
The DATA step preceding the Margins call creates a data set that specifies the desired contrasts of the A,B margins. This data set is specified in contrasts= and must contain the LABEL and F character variables. The first contrast, labeled A1-A0, defines a two row contrast matrix. Each row defines an A1-A0 difference – first in B1, then in B0. The second contrast defines the difference in difference, (A1B1-A0B1)-(A1B0-A0B0):
data c;
length label f $32767;
infile datalines delimiter='|';
input label f;
datalines;
A1-A0 | 0 -1 0 1, -1 0 1 0
Diff in Diff of Means | 1 -1 -1 1
;
%Margins(data = a,
response = y,
roptions = event='1',
class = a b,
classgref= first,
model = a|b,
dist = binomial,
margins = a b,
contrasts= c,
options = cl)
The Predictive Margins table reproduces the mean estimates shown above from the LSMEANS/ILINK statement in PROC LOGISTIC. The Contrasts table provides, for each of the two contrasts, a joint chi-square test and an estimate and test for each row in the contrast. The A1-A0 difference in B1 is 0.07 and is not significant (p=0.3210). The A1-A0 difference in B2 is 0.33 and is significant (p<0.0001). The joint test of the A difference with 2 degrees of freedom is also significant (p<0.0001). Finally, the estimated difference in difference is -0.26 and is significant (p=0.0072):
 |
Using the NLMeans Macro
While the difference in difference contrast of means cannot be estimated by the ESTIMATE statement as noted above, it can also be estimated using the NLMeans macro (SAS Note 62362). To use the macro, you need to supply the saved model from the STORE statement and a data set of coefficients that define the individual LS-means. This coefficients data set is made available by the E option in the LSMEANS statement and is saved by the ODS OUTPUT statement shown above. Finally, create a data set that contains the desired contrast of means (or contrasts, if you want to estimate several). The data set must contain variables named SET and K1, K2, ... , Kn, where n is the number of means estimated by the LSMEANS statement. In this case, n=4. The SET variable is primarily used when multiple sets of means are estimated by the SLICE statement or by multiple LSMEANS, SLICE, or ESTIMATE statements. Since there is only a single LSMEANS statement and therefore only a single set of LS-means, SET=1.
These statements then create the data set containing the difference in difference contrasts and call the NLMeans macro. Note that you need to specify the link function used in the fitted model, which is the logit function for a logistic model:
data difdif;
input k1-k4;
set=1;
datalines;
1 -1 -1 1
;
%NLMeans(instore=log, coef=coeffs, link=logit, contrasts=difdif,
title=Difference in Difference of Means)
The estimated difference in differences of means (probabilities) is -0.26 ≅ (0.53-0.46)-(0.72-0.39) with large-sample confidence interval (-0.45, -0.07):
|
Using the NLEST Macro
Next, the NLEST macro (SAS Note 58775) is used. The model saved using the STORE statement is again used in the macro. The expression for the difference in differences of means estimate can be directly specified in the f= option. The parameter names that the macro uses are B_px, where x=1, 2, 3,... in the order shown in the Parameter Estimates table. The Intercept is B_p1. The A parameter is B_p2. B_p4 is the B parameter, and the interaction parameter is B_p6:
%nlest(instore=log,
label=Diff in Diff Means,
f=( logistic(b_p1+b_p2+b_p4+b_p6) - logistic(b_p1+b_p4) ) -
( logistic(b_p1+b_p2) - logistic(b_p1) ),
title=Difference in Difference of Means)
The results are the same as from the NLMeans macro above:
|
Difference in Difference Analysis in a Pre/Post Longitudinal Study
Consider a longitudinal study of independent exposed and unexposed groups with 100 subjects in each. The following statements generate data similar to what might come from such a study in which the subject has a binary response (0 or 1) before and after an intervention:
data a;
do Exposed=1,0;
input mean_post mean_pre @;
do ID=1 to 100;
Y_post=ranbin(23425,1,mean_post);
Y_pre=ranbin(23425,1,mean_pre);
output;
end;
end;
datalines;
.5 .7 .4 .4
;
As in the previous example, these statements rearrange the data and fit an appropriate logistic GEE model:
data a;
keep exposed id post y;
set a;
Post=1; y=y_post; output;
Post=0; y=y_pre; output;
run;
proc genmod;
class id exposed post / ref=first;
model y(event="1") = exposed post exposed*post / dist=bin;
repeated subject=id(exposed);
estimate "DID Post(E-U)-Pre(E-U)" exposed*post 1 -1 -1 1;
lsmeans exposed*post / e ilink;
ods output coef=coeffs;
lsmestimate exposed*post "DID Post(E-U)-Pre(E-U)" 1 -1 -1 1;
store log;
run;
The Margins macro can also be used for the difference in difference analysis of a longitudinal study. The macro can fit the same logistic GEE model by including GEESUBJECT= (and for some studies, GEEWITHIN= and/or GEECORR=):
data c;
length label f $32767;
infile datalines delimiter='|';
input label f;
datalines;
Exposed-Unexposed | 0 -1 0 1, -1 0 1 0
DID Post(E-U)-Pre(E-U) | 1 -1 -1 1
;
%Margins(data = a,
response = y,
roptions = event='1',
class = id exposed post,
classgref = first,
model = exposed|post,
dist = binomial,
geesubject = id(exposed),
margins = exposed post,
contrasts = c,
options = cl)
Estimating the Difference in Difference for Other GLMs
The Margins, NLMeans, or NLEST macro can similarly be used to estimate the difference in differences of means for generalized linear models that use other link functions. For example, the log link is commonly used for modeling count responses in Poisson and negative binomial models. It is also typical in gamma models for positive, continuous responses. The difference in differences of means estimate for log-linked models is done as for the logistic model above, but specifying the log link in the NLMeans macro. With the NLEST macro, the EXP function is used in the f= expression rather than the LOGISTIC function since exponentiation is the inverse of the log.
Estimating the Difference in Difference in Models with Covariates
In models with covariates, the default estimate of the difference in difference provided by the LSMESTIMATE statement (for identity-linked models) or NLMeans macro (for other links) is an estimate at the mean of any continuous covariate and averaged over the balanced levels of any categorical (CLASS) covariate. You can see this by examining the table of coefficients that define the LS-means produced by the E option in the LSMEANS statement. In that table, note the coefficients for the covariates in the model.
To estimate the difference in difference at values other than the means of continuous covariates, specify the AT option in the LSMEANS statement. To estimate the difference in difference over the levels of categorical covariates using unequal proportions, specify the OM option in the LSMEANS statement. To use proportions equal to those observed in the input data, specify the OM option. To specify other unequal proportions, specify the OM=data-set option and specify the name of a data set that exhibits the desired proportions.
In the above example, suppose that the model contains additional covariates – a continuous covariate, C, as well as one or more categorical covariates. To estimate the difference in difference at C=2.5 and at the proportions of the categorical covariates (for each A,B combination) as found in data set FixProps, specify the following LSMEANS statement:
lsmeans a*b / e ilink at c=2.5 om=FixProps;
However, if the difference in difference is estimated using predictive margins rather than LS-means, no change is needed in the call to the Margins macro other than to include the covariates in the model specification. Note that predictive margins are averages of predicted values produced using the observed values of the covariates rather than fixing them as done for LS-means.
To estimate the difference in difference separately within the levels of a categorical covariate, include interactions in the model between the covariate and both variables involved in the difference in difference and their interaction. In the above example, suppose that difference in difference estimates are desired at each level of a categorical covariate, C, that has three levels. The following modification to the logistic model allows the difference in difference to vary across the levels of C. The modified LSMEANS statement provides mean estimates at each of the 12 combinations of C, A, and B:
model y(event="1") = c|a|b;
lsmeans c*a*b / e ilink;
Note that the above model is a short-hand specification that is equivalent to specifying c a b c*a c*b a*b c*a*b. The following contrasts define the difference in difference at each of the three levels of C. The NLMeans macro then provides difference in difference estimates at each level of C:
data difdif;
input k1-k12;
set=1;
datalines;
1 -1 -1 1 0 0 0 0 0 0 0 0
0 0 0 0 1 -1 -1 1 0 0 0 0
0 0 0 0 0 0 0 0 1 -1 -1 1
;
%NLMeans(instore=log, coef=coeffs, link=logit, contrasts=difdif,
title=Difference in Difference of Means)
This can also be done using the Margins macro, but a separate call of the macro is needed to estimate the difference in difference at each level of the covariate. No modification is needed to the contrasts data set, C, shown above preceding the Margins macro call. The Margins macro call is modified as follows to add the covariate and interactions in the model as noted above, and to add within= to request the difference in difference estimate at the C=1 level. Similar calls to the Margins macro can be used to obtain estimates at the other levels of the covariate:
%Margins(data = a,
response = y,
roptions = event='1',
class = c a b,
model = c|a|b,
dist = binomial,
margins = a b,
contrasts= c,
within = c=1,
options = cl)
Operating System and Release Information
| Product Family | Product | System | SAS Release | |
| Reported | Fixed* | |||
| SAS System | SAS/STAT | z/OS | ||
| z/OS 64-bit | ||||
| OpenVMS VAX | ||||
| Microsoft® Windows® for 64-Bit Itanium-based Systems | ||||
| Microsoft Windows Server 2003 Datacenter 64-bit Edition | ||||
| Microsoft Windows Server 2003 Enterprise 64-bit Edition | ||||
| Microsoft Windows XP 64-bit Edition | ||||
| Microsoft® Windows® for x64 | ||||
| OS/2 | ||||
| Microsoft Windows 8 Enterprise 32-bit | ||||
| Microsoft Windows 8 Enterprise x64 | ||||
| Microsoft Windows 8 Pro 32-bit | ||||
| Microsoft Windows 8 Pro x64 | ||||
| Microsoft Windows 8.1 Enterprise 32-bit | ||||
| Microsoft Windows 8.1 Enterprise x64 | ||||
| Microsoft Windows 8.1 Pro 32-bit | ||||
| Microsoft Windows 8.1 Pro x64 | ||||
| Microsoft Windows 10 | ||||
| Microsoft Windows 95/98 | ||||
| Microsoft Windows 2000 Advanced Server | ||||
| Microsoft Windows 2000 Datacenter Server | ||||
| Microsoft Windows 2000 Server | ||||
| Microsoft Windows 2000 Professional | ||||
| Microsoft Windows NT Workstation | ||||
| Microsoft Windows Server 2003 Datacenter Edition | ||||
| Microsoft Windows Server 2003 Enterprise Edition | ||||
| Microsoft Windows Server 2003 Standard Edition | ||||
| Microsoft Windows Server 2003 for x64 | ||||
| Microsoft Windows Server 2008 | ||||
| Microsoft Windows Server 2008 R2 | ||||
| Microsoft Windows Server 2008 for x64 | ||||
| Microsoft Windows Server 2012 Datacenter | ||||
| Microsoft Windows Server 2012 R2 Datacenter | ||||
| Microsoft Windows Server 2012 R2 Std | ||||
| Microsoft Windows Server 2012 Std | ||||
| Microsoft Windows Server 2016 | ||||
| Microsoft Windows XP Professional | ||||
| Windows 7 Enterprise 32 bit | ||||
| Windows 7 Enterprise x64 | ||||
| Windows 7 Home Premium 32 bit | ||||
| Windows 7 Home Premium x64 | ||||
| Windows 7 Professional 32 bit | ||||
| Windows 7 Professional x64 | ||||
| Windows 7 Ultimate 32 bit | ||||
| Windows 7 Ultimate x64 | ||||
| Windows Millennium Edition (Me) | ||||
| Windows Vista | ||||
| Windows Vista for x64 | ||||
| 64-bit Enabled AIX | ||||
| 64-bit Enabled HP-UX | ||||
| 64-bit Enabled Solaris | ||||
| ABI+ for Intel Architecture | ||||
| AIX | ||||
| HP-UX | ||||
| HP-UX IPF | ||||
| IRIX | ||||
| Linux | ||||
| Linux for x64 | ||||
| Linux on Itanium | ||||
| OpenVMS Alpha | ||||
| OpenVMS on HP Integrity | ||||
| Solaris | ||||
| Solaris for x64 | ||||
| Tru64 UNIX | ||||
| Type: | Usage Note |
| Priority: | |
| Topic: | Analytics ==> Regression Analytics ==> Transformations SAS Reference ==> Procedures ==> GENMOD SAS Reference ==> Procedures ==> GLIMMIX SAS Reference ==> Procedures ==> GLM SAS Reference ==> Procedures ==> LOGISTIC SAS Reference ==> Procedures ==> MIXED SAS Reference ==> Procedures ==> ORTHOREG SAS Reference ==> Macro |
| Date Modified: | 2024-01-24 09:49:48 |
| Date Created: | 2018-02-09 15:20:07 |