Sample 62362: Estimate and test differences, ratios, contrasts, or other functions of means in generalized linear models
 |  |  |  |  |
Estimate and test differences, ratios, contrasts, or other functions of means in generalized linear models
| Contents: | Purpose / History / Requirements / Usage / Details / Limitations / See Also |
NOTE: Beginning in SAS® 9.4M6 (TS1M6), a version of this macro is available in the SAS/STAT® Autocall library and does not need to be downloaded and defined before use. To access features in more recent versions of the macro (see History), download and run as described in Usage below.
- PURPOSE:
- Provide multiple comparisons (pairwise, sequential, or against a control) on the mean scale among one or more sets of estimates produced from a model using a nonidentity link function on the response mean. More complex contrasts of means, ratios of pairs of means, or other linear or nonlinear functions of means can also be estimated and tested.
- HISTORY:
- The version of the NLMEANS macro that you are using is displayed in the log when you specify anything as the first argument. For example:
%nlmeans(v)The NLMEANS macro always attempts to check for a later version of itself. If it is unable to do this (such as if there is no active internet connection available), the macro will issue the following message in the log:
NOTE: Unable to check for newer version of the NLMEANS macro.
The computations performed by the macro are not affected by the appearance of this message. However, this check can be avoided by specifying nochk as the first macro argument. This can be useful if your machine has no connection to the internet.
Version Update Notes 3.2 Fix when NLMeans is called in a macro loop using &i or &s as an index macro variable. 3.1 Now allows estimation of multinomial probabilities in intercepts-only models. 3.0 Added f=, fset=, flabel=, and fdata=. Fixed behavior of options=joint with multinomial models. Enhanced flexibility with contrasts= and multinomial models. Requires version 2.1 or later of the NLEST macro. NLMeans version 3.0 is available in the SAS/STAT Autocall Library beginning in SAS 9.4M9 (TS1M9). 2.0 nochk can be specified as the first (version) parameter. Requires version 2.1 or later of the NLEST macro. 1.4 Added where= and covdrop=. Requires version 1.9 or later of the NLEST macro. Version 1.4 of NLMeans and version 1.9 of NLEST are available in the SAS/STAT Autocall Library beginning in SAS 9.4M8 (TS1M8). 1.3 Added print | noprint to options=. Added null=. Requires version 1.8 or later of the NLEST macro. 1.04, 1.1 Store sets of results in data sets EST1, EST2, ... . Append all sets into a single results file using options=append. Version 1.1 of NLMeans and version 1.6 of NLEST are available in the SAS/STAT Autocall Library beginning in SAS 9.4M6 (TS1M6). 1.03 Fix for LABEL variable in contrasts= data set. 1.02 Minor fix to version printing. 1.01 A LABEL variable can optionally be included in the contrasts= data set. 1.0 Initial coding - REQUIREMENTS:
- Base SAS®, SAS/STAT®, and the NLEST (SAS Note 58775) are required. See History above.
- USAGE:
- Follow the instructions on the Downloads tab of this sample to save the NLMEANS macro definition. Follow similar instructions to download and define the NLEST macro (SAS Note 58775). Replace the text within quotation marks in the following statements with the locations of the NLMEANS and NLEST macro definition files on your system. In your SAS program or in the SAS editor window, specify these statements to define both macros and make them available for use in your SAS session:
%inc "<location of your file containing the NLEST macro>"; %inc "<location of your file containing the NLMEANS macro>";
After defining both macros in your SAS session, fit your model and include one or more LSMEANS, SLICE, ESTIMATE, or LSMESTIMATE statements with the E option and save the model using the STORE statement. You can then call the NLMEANS macro to estimate and test functions of response means. See the Results tab for examples.
The following parameters are required when using the NLMEANS macro. The necessary model information is provided to the macro by specifying either the instore= parameter or both the inest= and incovb= parameters. If the modeling procedure provides a STORE statement for saving the fitted model, instore= is generally the better method for providing the model information.
- instore=item-store
- Specifies the fitted model that was saved using the STORE statement in the modeling procedure. The OUT= option in the STORE statement saves the model in a file known as an item store. This is the preferred method for providing the required model information. However, if the modeling procedure does not offer the STORE statement, then you might be able to use inest= and incovb= instead. See "Limitations" below.
... or both of the following ...
inest=data-set-name- Specifies the data set of parameter estimates saved using an ODS OUTPUT statement in the modeling procedure. The parameter estimates of the model should be stored in a variable named ESTIMATE in this data set. An error is issued if the ESTIMATE variable is not found. When inest= is specified, incovb= must also be specified. The parameter vector in the inest= data set must be compatible with the covariance matrix in the incovb= data set. See "Compatibility error when using inest= and incovb=" below.
- incovb=data-set-name
- Specifies the data set containing the variance-covariance matrix of model parameters saved using an ODS OUTPUT statement in the modeling procedure. Typically, an option such as COVB is required in the modeling procedure to make this matrix available for saving. When inest= is specified, incovb= must also be specified. The parameter vector in the inest= data set must be compatible with the covariance matrix in the incovb= data set. See "Compatibility error when using inest= and incovb=" below.
The following parameters are also required.
coef=data-set-name- Specifies the data set of estimate coefficients saved using an ODS OUTPUT statement in the modeling procedure. The required table(s) must first be produced by including the E option in the LSMEANS, SLICE, ESTIMATE, or LSMESTIMATE statement in the modeling procedure. The data set must contain the following variables: Parameter (or Effect), LMatrix, Row1 and any number of additional variables: Row2, Row3, ... . Note that the resulting data set contains multiple sets of estimates (displayed in multiple tables) when there are multiple variables in the LSMEANS statement, the SLICEBY= option is used in the SLICE statement, or there are multiple LSMEANS, SLICE, ESTIMATE, or LSMESTIMATE statements. The estimate sets are indexed by the LMatrix variable in this data set. The table name is typically Coef and can be saved in a data set by specifying:
ods output Coef=data-set-name; - link=link-function
- Specifies the link function used in the modeling procedure, typically in the LINK= option in the MODEL statement. Note that for models fit by PROC PROBIT, which specifies the link with the DIST= option, specify link=probit, normit, or cumprobit when DIST=NORMAL; link=logit or cumlogit when DIST=LOGISTIC; or link=cll or cumcll when DIST=EXTREME or GOMPERTZ. The ALOGIT link is not supported.
Estimation and testing of functions of response means, such as pairwise differences or ratios, or other linear or nonlinear functions of means can be requested using any of the following. By default, diff=all. When contrasts= is specified, diff= is ignored. contrasts= is not available with multinomial models.
- diff=type <type> ...
where type is all, seq, or number - To estimate and test all pairwise differences of means, specify diff=all. Sequential differences of means (μ1-μ2, μ2-μ3, ...) are provided when diff=seq. To obtain all differences with a control level, specify diff=number, where number is the position of the control level in the ordered list of levels shown in the results from the modeling procedure. For example, if level A is the control in a variable whose levels are shown in the order A, B, C, then specify diff=1. When there are multiple sets of estimates from the modeling procedure (presented in multiple tables) saved in the coef= data set, you can either specify a single type to apply to all estimate sets, or a list of types to apply a different type to each of the sets. If diff= is omitted, all pairwise differences are done for all sets (diff=all). If diff= and contrasts= are both specified, diff= is ignored. See the Examples in the Results tab.
- contrasts=data-set-name
- Specifies an optional data of coefficients defining contrasts among the estimates in each set of estimates. The specified data set must contain a variable named SET and k variables named K1, K2, ... , Kk, where k is the number of Row variables in coef= data set. Optionally, a LABEL variable can be included to label each of the specified contrasts. For a given row in the data set, the value of SET indicates the set of estimates that the contrast in that row applies to. The SET value must match one of the values of the LMatrix variable in the coef= data set. The K variables correspond to the Row variables in the coef= data set, which define each estimate. Multinomial models are fit to f response functions such as logits. For ordinal models, k=mf where m is the number of estimates in each response function. For nominal, link=glogit models, k=mf+m, where the additional set of m variables corresponds to the last response level. See Multinomial models in Details below. See the description of options=ratio for limitations on the contrast coefficients when mean ratios are desired. If contrasts= and diff= are both specified, diff= is ignored. contrasts= is not available with multinomial models when options=joint is specified. Use f= or fdata= instead. See Example 2 in the Results tab.
- f=expression
- Requires version 3.0 or later of the NLMEANS macro and version 2.1 or later of the NLEST macro. Specifies a linear or nonlinear function of the available response means to be estimated and tested, where the means should be referred to as mu1, mu2, ... , muk where k is the number of estimates produced by the LSMEANS, SLICE, ESTIMATE, or LSMESTIMATE statements in the model fitting step. The ordering of the mean names corresponds to the order of the estimates in the output from the modeling procedure. The expression can involve mathematical functions (such as log(·), exp(·), and so on). An example of a valid expression is f=log((mu1/mu5)/(mu2/mu6)). See Examples 2 and 3 in the Results tab.
- fset=number
- Requires version 3.0 or later of the NLMEANS macro and version 2.1 or later of the NLEST macro. When there are multiple estimate sets in the coef= data set, fset= is required to indicate the set to which the function of means defined by f= should be applied. number should be an integer, 1, 2, ... , s, where s is the number of sets that appear in coef=. Set numbers are shown in the LMatrix variable in the coef= data set and number should match one of those values. Note that sets are numbered in the order in which they appear in the modeling procedure output and not necessarily in the order of the submitted statements. See Examples 2 and 3 in the Results tab.
- flabel=label
- Requires version 3.0 or later of the NLMEANS macro and version 2.1 or later of the NLEST macro. Optionally provides a label to be displayed with the estimate and test of the function defined in f=. label must not contain quotation marks (" or '), ampersands (&), commas, or parentheses. See Examples 2 and 3 in the Results tab.
- fdata=data-set-name
- Requires version 3.0 or later of the NLMEANS macro and version 2.1 or later of the NLEST macro. Specifies a data set containing one or more functions of means to be estimated. fdata= is most useful when you have more than one function to estimate. This data set must contain a character variable, F, and a numeric variable, SET. Optionally, a character variable, LABEL, can be included. In each observation of the data set, F contains an expression defining a function of response means. The expression should appear in the same way as described in f=. If included, LABEL contains a text string used to label the estimated function in the results and should not be enclosed in or contain quotation marks. If omitted, the expression in F is used as a label. The SET value should indicate the estimate set that the function in F applies to. See Example 2 in the Results tab.
The following parameters are optional:
- where=condition
- Requires version 1.4 or later of the NLMEANS macro and version 1.9 or later of the NLEST macro. Specifies an optional condition to subset the inest=, incovb=, and coef= data sets. Condition is a valid expression for the WHERE statement and is useful when the input data sets were created using a BY statement or, in survey analysis, when the DOMAIN statement was used. See Example 4 in the Results tab.
- covdrop=variable(s)
- Requires version 1.4 or later of the NLMEANS macro and version 1.9 or later of the NLEST macro. Specifies one or more variables to be dropped from the incovb= data set. This can be helpful when an error occurs indicating that the covariance matrix is incompatible with the parameter vector. That error is often caused by the presence of numeric variables in the incovb= data set that do not contain columns of the covariance matrix.
- null=value
- Requires version 1.3 or later of the NLMEANS macro and version 1.8 or later of the NLEST macro. Specifies value in the null hypothesis H0: f(μ)=value, where f(μ) is the function of means being tested and value is a numeric value. Scientific notation, such as 1E4, is not allowed. The default is null=0. See Example 1 in the Results tab.
- df=value
- Specifies the degrees of freedom to be used in the tests and confidence intervals computed for the estimated functions. value must be a non-zero, positive value. Scientific notation, such as 1E4 is not allowed. If omitted, large-sample Wald statistics are given. The degrees of freedom for testing a linear combination of parameters in a linear model would typically be the number of observations used in fitting the model minus the number of parameters estimated in the model – essentially, the error degrees of freedom.
- alpha=value
- Specifies the alpha level to be used in computing confidence limits. If omitted, alpha=0.05.
- title=title-text
- Specifies a title for the table(s) of results. The title-text must not contain quotation marks (" or '), ampersands (&), commas, or parentheses. If omitted, title=Nonlinear Function Estimate. See the Examples in the Results tab.
- options=<JOINT|NOJOINT> <NAMES|NONAMES> <REVERSE|NOREVERSE> <RATIO|NORATIO> <DIFINFNS|DIFALL> <APPEND|NOAPPEND> <PRINT|NOPRINT>
- Use options= to enable or disable any of several binary options. If not specified, options=nojoint nonames noreverse noratio difinfns noappend print.
JOINT combines multiple sets of estimates into a single set before differencing or applying contrasts. See Example 3 in the Results tab and SAS Note 70221.
NAMES displays the names of the model parameters used by the NLEST macro.
REVERSE reverses the direction of differencing done by diff=. REVERSE is ignored when contrasts=, f=, or fdata= is specified.
RATIO requests estimation of ratios rather than differences of pairs of means. RATIO can be used with diff= or contrasts=, but with contrasts= each contrast must specify exactly one 1 coefficient to select the numerator, one -1 coefficient to select the denominator, and 0 coefficients otherwise. See Example 1 in the Results tab.
DIFALL can be used with multinomial models to apply the differencing type specified in diff= to means across all the response functions rather than within the response functions as done by the default DIFINFNS. This option is ignored for nonmultinomial models or when diff= is not used. See Example 2 in the Results tab.
APPEND merges results from all estimate sets into a single results data set named EST_ALL. NOAPPEND saves results sets in separate data sets (EST1, EST2, ...). The last results set is always saved in data set EST as well.
NOPRINT suppresses display of the results table (but does not suppress the table of parameter names if NAMES is also specified). Requires version 1.3 or later of the NLMEANS macro and version 1.8 or later of the NLEST macro.
- DETAILS:
- The NLMEANS macro can be used after fitting a Generalized Linear or Generalized Estimating Equations Model (GLM or GEE) and estimating multiple linear combinations of model parameters, Liβ, which are response means, μi, when the inverse of the link function, g, is applied. That is, μi = g-1(Liβ). Several SAS/STAT modeling procedures can be used including GENMOD, GLIMMIX, LOGISTIC, PROBIT, SURVEYLOGISTIC, and GEE. Liβ estimates are available using the LSMEANS or SLICE statement in the modeling procedure. The ESTIMATE and LSMESTIMATE statement can also be used, but only if they estimate one or more individual g(μi) and not functions of two or more g(μi) such as differences or other linear combinations. The ILINK option can be used in these statements to display estimates of the means, μi, in the procedure output.
While the DIFF option in the LSMEANS and SLICE statements provide pairwise differences on the link scale, Liβ-Ljβ, differences on the mean scale, μi-μj, are not available. Similarly, in an ESTIMATE or LSMESTIMATE statement that defines a difference, Liβ-Ljβ, the ILINK option applies the inverse of the link function to the difference, g-1(L1β-L2β) rather than computing the difference of the inverse linked estimates g-1(L1β)-g-1(L2β) = μi-μj. The same situation applies to estimating functions that are more complex than a simple difference. The NLMEANS macro is provided to make estimation of these functions available on the mean scale rather than the link scale. Note that the quantity g-1(L1β-L2β) is generally only of interest in the case where the link function, g, is the log. In this case, the ILINK or EXP option estimates the ratio of means.
Note that the NLMEANS macro is not needed for models that use the identity link. This includes models fit by the REG, GLM, MIXED, or ORTHOREG procedures and others. For these models, μi=Liβ, so differences or other functions of the Liβ are equivalent functions of the μi. Consequently, the results of the DIFF option in the LSMEANS or SLICE statement, or the results of an ESTIMATE or LSMESTIMATE statement that defines a function of the Liβ directly provide the same function of the μi.
The NLMEANS macro can be used to provide estimates and tests of differences of means, μi-μj, ratios of means, μi/μj, or linear contrasts of means. Using f= or fdata=, even nonlinear functions of means can be estimated. Standard errors are obtained using the delta method. To use the macro, you supply the saved model and a data set containing the coefficients, Li, used by one or more LSMEANS, SLICE, ESTIMATE, or LSMESTIMATE statements. You also indicate the link function used in the model. The model is best saved using the STORE statement in the modeling procedure. The coefficients can be saved by including the E option in any LSMEANS, SLICE, ESTIMATE or LSMESTIMATE statement(s) specified in the procedure, and by including an ODS OUTPUT statement to save the displayed table of coefficients in a data set. In most procedures, the name of the coefficients table is Coef, so the following statement saves it in a data set.
ods output coef=data-set-name;
See the list of macro parameters above for details about how to provide the saved model and coefficients to the macro, about how to request differences, ratios, contrasts, or other functions of means as well as other options.
The macro can process one or more sets of estimates. Multiple sets of estimates occur when the modeling procedure includes an LSMEANS statement with multiple variables, a SLICE statement with the SLICEBY= option, or multiple LSMEANS, SLICE, ESTIMATE, or LSMESTIMATE statements. The macro estimates the requested function(s) in each set and a table of results is displayed for each set of estimates. If you want to estimate function(s) of means defined across multiple sets, you can use options=joint to combine all of the separate sets into a single set.
Multinomial Models
For ordinal multinomial models (link=cumlogit, cumprobit, cumloglog, cumcloglog), the estimated means in any population are cumulative probabilities, Pr(Y=1), Pr(Y≤2), ... , Pr(Y≤ l), where l is the number of cumulative response functions, which is one less than the number of levels in the response variable, Y. For nominal multinomial models (link=glogit), the estimated means in any population are individual level probabilities, Pr(Y=1), Pr(Y=2), ... , Pr(Y= l ), where l is the number of response levels.
When diff= is specified in a multinomial model to provide pairwise comparisons in an estimate set (such as among levels of a variable in the LSMEANS statement), the macro by default estimates the requested comparisons within each of the l response functions or levels. This is the action with the default options=difinfns. For example, an ordinal cumulative logit model (link=cumlogit) on a three-level response has l = 2 cumulative logit response functions and predicts each of two cumulative probabilities (means). The requested comparisons are estimated separately for each cumulative mean. For a nominal multinomial model on a three-level response, by default the requested differences are estimated separately for each of the l = 3 individual response level probabilities (means). If you specify options=difall with diff=, the differencing method is applied across all k=ml probabilities, where m is the number of estimates in the estimate set. If you want to estimate differences or other functions defined across all the k means in an estimate set, you can use contrasts=, f=, or fdata=. See Example 2 in the Results tab.
When specifying a contrasts= data set, each contrast (row) of the data set can contain coefficients for all k=ml means. However, if you want the same contrasts to be applied separately to the m means within each response function or level, then you can specify just k=m coefficients and the macro will duplicate the provided coefficients in each of the l response functions or levels. Again, see Example 2 in the Results tab.
Output Data Sets
When the NLMEANS macro processes a single set of estimates (such as from a single LSMEANS statement), results are automatically saved in data set EST. When multiple sets of estimates are processed, the results from each set are saved by default in separate data sets named EST1, EST2, EST3, ... . Specify options=append to create a single data set named EST_ALL of all results from all sets. Be aware that if EST_ALL already exists, new results are appended to it. The last results set is also stored in data set EST.
BY Group or Domain Processing
The NLMEANS macro does not directly support BY group processing (such as for the analysis of multiply imputed data) or processing of domains from a survey analysis. That is, it cannot process results from a modeling procedure that was run using a BY or DOMAIN statement. However, this capability can be provided by the RunBY macro, which can run the NLMEANS macro repeatedly for each of the BY groups or domains. Version 1.4 or later of the NLMEANS macro, version 1.9 or later of the NLEST macro, and version 1.1 or later of the RunBY macro are required. See the RunBY macro documentation (SAS Note 66249) for details about its use. Additionally, you can use where= to allow NLMEANS to process the results of one BY group or domain by specifying an appropriate condition to select that BY group or domain. See the Example 4 in the Results tab above.
Troubleshooting Hessian Warning
Since the LSMEANS and SLICE statements require GLM parameterized CLASS variables (PARAM=GLM in the CLASS statement), the NLEST macro (which is called by the NLMEANS macro) will typically display the following Warning message in this log. This Warning can be ignored when it is caused by the use of GLM parameterization.
WARNING: The final Hessian matrix is not positive definite, and therefore the estimated covariance matrix is not full rank and may be unreliable. The variance of some parameter estimates is zero or some parameters are linearly related to other parameters.Compatibility Error when Using inest= and incovb=
Specifying inest= and incovb= instead of instore= is generally not necessary. If used, modifications of those data sets or use of where= and/or covdrop= might be needed to correct incompatibility of the parameter vector and covariance matrix. In some cases, it might be necessary to use the NLEST macro directly rather than NLMEANS.
The incovb= data set should have the same number of observations (rows) and variables (columns) as the number of rows in the inest= data set in order to be compatible. Otherwise, an error message is issued that indicates the relevant numbers of rows and columns. If the incovb= data set contains numeric variables other than those containing the covariance matrix, they should be removed in order to avoid a compatibility error. This can be done either by preprocessing the data set to remove the extraneous variables or by specifying them in covdrop= (requires version 1.4 or later of the NLMEANS macro and version 1.9 or later of the NLEST macro).
Warnings Concerning AdditionalEstimates, df, and Probt
If a requested function of means results in a computational error, such as division by zero or taking the log of a negative value, the macro will issue Warning messages in the log indicating that 'AdditionalEstimates' was not created and that variables df and Probt were never referenced. No results are presented for the estimate set where this occurs even if other functions in the set are estimable.
- LIMITATIONS:
- The NLMEANS macro is not intended for use with models from PROC CATMOD, or from SAS/ETS® procedures. The macro cannot be used to compare means from zero-inflated models fit by PROC GENMOD.
Some modeling procedures cannot provide the necessary covariance matrix for some models. Some procedures either do not have a STORE statement (such as PROC FMM) or do not save the necessary model information (such as PROC COUNTREG). In such cases, use inest= and incovb= instead of instore=. When using inest= and incovb=, incompatibility of the parameter vector and covariance matrix can occur. See Compatibility error when using inest= and incovb= above.
For some models, such as those fit by the GENMOD or GLIMMIX procedures, use of the LSMEANS, SLICE, ESTIMATE, or LSMESTIMATE statements in the PLM procedure is recommended rather than using those statements in the modeling procedure. Using those statements in PLM requires saving the fitted model using the STORE statement in the modeling procedure.
Each coefficient column vector in an estimate set (identified by the LMatrix variable) appearing in the coef= data set should estimate an individual, link-transformed mean, g(μi). The NLMEANS macro applies the inverse of the link function specified in link= to obtain the means, μi, to be used in estimating the functions requested using the various macro parameters described above.
- SEE ALSO:
- The NLMEANS macro forms the expressions to be evaluated. It then calls the NLEST macro to do the computations. See the NLEST macro description (SAS Note 58775) for details. The Margins macro (SAS Note 63038) can also be used to estimate and test differences or contrasts of means. Unlike the NLMEANS macro, the Margins macro can be used when one or more predictors in the model is not held fixed.
These sample files and code examples are provided by SAS Institute Inc. "as is" without warranty of any kind, either express or implied, including but not limited to the implied warranties of merchantability and fitness for a particular purpose. Recipients acknowledge and agree that SAS Institute shall not be liable for any damages whatsoever arising out of their use of this material. In addition, SAS Institute will provide no support for the materials contained herein.
These sample files and code examples are provided by SAS Institute Inc. "as is" without warranty of any kind, either express or implied, including but not limited to the implied warranties of merchantability and fitness for a particular purpose. Recipients acknowledge and agree that SAS Institute shall not be liable for any damages whatsoever arising out of their use of this material. In addition, SAS Institute will provide no support for the materials contained herein.
In addition to the examples below, several more examples of using the NLMEANS macro can be found in these notes:
- Estimating differences in probabilities with confidence interval (SAS Note 37228)
- Estimating rate differences (with confidence interval) using a Poisson model (SAS Note 37344)
- Estimating relative risks in a multinomial response model (SAS Note 57798)
- Estimating a relative risk (also called risk ratio, prevalence ratio) (SAS Note 23003)
- Estimating the difference in differences of means (SAS Note 61830)
- Estimating the risk (proportion) difference for matched pairs data with binary response (SAS Note 46997)
- Estimate and plot the effect of changing a continuous predictor in a spline (SAS Note 70221)
- Compare group slopes on a continuous predictor in a spline or polynomial effect (SAS Note 70756)
- Tests, confidence intervals, and comparisons of multinomial variable probabilities (SAS Note 32609)
- EXAMPLE 1: Estimate the difference or ratio of group means in a log-linked gamma model
The example titled "Gamma Distribution Applied to Life Data" in the PROC GENMOD documentation presents failure times of 201 machine parts from two manufacturers, denoted A and B. The following GENMOD statements fit the log-linked gamma model. The STORE statement saves the model in an item store for later use by the NLMEANS macro. The LSMEANS statement with the ILINK option is used in PROC PLM to estimate the manufacturer means.
proc genmod data = lifdat; class mfg / param=glm; model lifetime = mfg / dist=gamma link=log; store out=gammod; run; proc plm restore=gammod; lsmeans mfg / e ilink diff exp; ods output coef=coeffs; run;In the partial results below, the intercept, MFGA, and MFGB estimated model parameters are shown in the "Analysis Of Maximum Likelihood Parameter Estimates" table. The values in the Estimate column in the "MFG Least Squares Means" table are the estimates of the linear combinations of model parameters, Liβ, defined in the "Coefficients for MFG Least Squares Means" table. This table of coefficients is produced by the E option and will be needed by the NLMEANS macro. From this table it can be seen that the MFG="A" estimate, 6.1501, is the Row1 linear combination defined as 1*Intercept+1*MFGA. Similarly for MFG="B". Note that since the linear predictor in this gamma model estimates the log gamma mean, linear combinations of the model parameters, such as those from the LSMEANS or ESTIMATE statement, also estimate the log gamma mean. Therefore, 6.1501 is the estimated log mean for manufacturer A. 6.1302 is the estimated log mean for manufacturer B. The ILINK option in the LSMEANS statement applies the inverse of the link function to the estimates. In this log-linked model, that means that the estimates are exponentiated. The resulting mean estimates are presented in the column labeled "Mean". The estimated mean lifetimes are 468.74 for manufacturer A and 459.51 for manufacturer B. The DIFF option computes the pairwise differences among the LS-mean estimates and presents them in the "Differences of MFG Least Squares Means" table. This produces a difference of the log means, or equivalently a log ratio of means, in the Estimate column (0.01989). The EXP option exponentiates this difference producing in an estimated ratio of means in the Exponentiated column (1.0201). Note that the EXP option also exponentiates the estimates in the "MFG Least Squares Means" table resulting in the Exponentiated column that reproduces the Mean column from the ILINK option in this case.
Analysis Of Maximum Likelihood Parameter Estimates Parameter DF Estimate Standard
ErrorWald 95% Confidence Limits Wald Chi-Square Pr > ChiSq Intercept 1 6.1302 0.1043 5.9257 6.3347 3451.61 <.0001 MFG A 1 0.0199 0.1559 -0.2857 0.3255 0.02 0.8985 MFG B 0 0.0000 0.0000 0.0000 0.0000 . . Scale 1 0.8275 0.0714 0.6987 0.9800
Coefficients for MFG Least
Squares MeansParameter MFG Row1 Row2 Intercept 1 1 MFG A A 1 MFG B B 1
MFG Least Squares Means MFG Estimate Standard Error z Value Pr > |z| Mean Standard Error
of MeanExponentiated A 6.1501 0.1159 53.07 <.0001 468.74 54.3172 468.74 B 6.1302 0.1043 58.75 <.0001 459.51 47.9468 459.51
Differences of MFG Least Squares Means MFG _MFG Estimate Standard Error z Value Pr > |z| Exponentiated A B 0.01989 0.1559 0.13 0.8985 1.0201 The difference of the manufacturer means can be estimated by the NLMEANS macro. Before using the macro, both the NLMEANS macro and the NLEST macro that it calls must be defined in your current SAS session. Use the %INCLUDE statements described in the Usage section of the Details tab.
With the macros defined, you can now call the NLMEANS macro. The fitted model, saved by the STORE statement as gammod, is provided by instore= and the data set of coefficients defining the LS-means and saved by the ODS OUTPUT statement is provided by coef=. The link function used for this model is the log function. By default, diff=all meaning that all pairwise differences will be computed. Since there are two estimates, there is only one difference to estimate. A title for the table of results is supplied by title=. Note that quotation marks should not be used in the title.
%nlmeans(instore=gammod, coef=coeffs, link=log, title=Difference of MFG means)The estimated difference in lifetime means is 468.74 - 459.51 = 9.2309 with 95% large-sample confidence interval (-132.77, 151.23). The Label column displays the contrast applied to the mean estimates showing that the computed difference is MFGA-MFGB. Note that if the MFGB-MFGA difference is desired, then add options=reverse in the macro call.
Difference of MFG means
Label Estimate Standard Error Wald Chi-Square Pr > ChiSq Alpha Lower Upper 1 -1 9.2309 72.4517 0.016233 0.8986 0.05 -132.77 151.23 The ratio of means can also be provided by the NLMEANS macro. Since it is of interest to test that the ratio equals 1 rather than 0 (the default), null=1 is specified.
%nlmeans(instore=gammod, coef=coeffs, link=log, options=ratio, null=1, title=Ratio of MFG means)The Label (1 /1) indicates that the computed ratio is MFGA/MFGB. If preferred, the reciprocal of this ratio can be estimated by adding options=reverse in the macro call.
Notice that the estimated ratio, 1.0201, is identical to the estimate provided by the EXP option in the LSMEANS statement. The ratio does not significantly differ from 1, the null hypothesis value specified by null=1 (p=0.8995). A large-sample 95% confidence interval for the ratio is (0.7083, 1.3319).
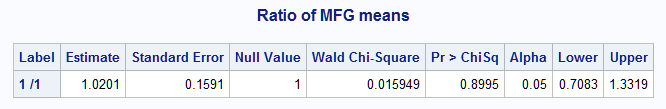
The difference in manufacturer means can also be produced by using the NLEST macro directly, though this requires writing the difference of means in terms of the model parameter estimates. This is illustrated in the Example in the Results tab of the NLEST macro description (SAS Note 58775).
- Example 2: Use of contrasts=, f=, fdata=, and options=difall in a multinomial model
-
The following uses the data in the example titled "Nominal Response Data: Generalized Logits Model" in the PROC LOGISTIC documentation about the teaching style preferred by students from three different schools in one of two programs. A nominal multinomial model is fit to the three-level Style response using the School and Program as predictors. The LSMEANS statement with the ILINK option is used to estimate the Program means, which are the probabilities of the Styles in each of the Programs. As discussed earlier, the DIFF option in the LSMEANS statement cannot estimate the differences between Programs on each of the Style probabilities, but this can be done with the NLMEANS macro.
proc logistic data=School; freq count; class Program / param=glm; model style(order=data) = Program / link=glogit; lsmeans Program / e ilink; ods output coef=coeffs; store out=logmod; run;Note that probabilities (in the "Mean" column) of only two of the three Style levels are estimated by the LSMEANS statement for each Program.
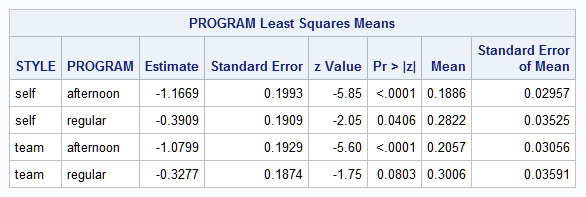
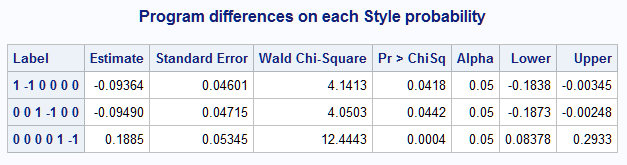
However, it is possible for the model to estimate each of the three Style probabilities in each of the two Programs for a total of six means. The NLMEANS macro can estimate functions of these six means. The order of the means is the same as displayed by the modeling procedure with the means of the last Style level considered as following those displayed. The default diff=all analysis by the NLMEANS macro compares the Programs on each of the three Style probabilities.
%nlmeans(instore=logmod, coef=coeffs, link=glogit, title=Program differences on each Style probability)Note the pattern of the pairwise differences indicated in the Label column. The Programs are compared first on the Pr(Style="self") then on Pr(Style="team") and finally on Pr(Style="class").
The equivalent of the default diff=all analysis can be done by specifying contrasts= with the three differencing contrasts in a data set. When you want the same set of contrasts to be applied to the means in each response level, the data set can include just one set of contrasts and the macro will repeat them in all response levels. Alternatively, you can specify the contrasts in all levels. The following shows both forms of contrasts= data set for comparing the Programs in each response level. The results from the macro call are identical to those above.
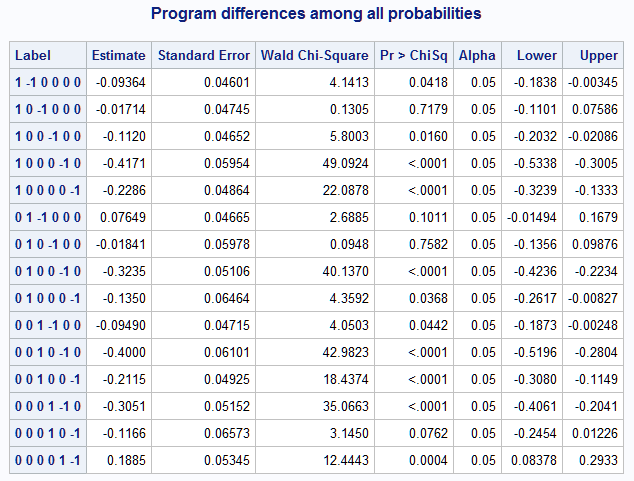
data c; set=1; infile datalines missover; input k1-k2; datalines; 1 -1 ; data c; set=1; infile datalines missover; input k1-k6; datalines; 1 -1 0 0 0 0 0 0 1 -1 0 0 0 0 0 0 1 -1 ; %nlmeans(instore=logmod, coef=coeffs, link=glogit, contrasts=c, title=Program differences on each Style probability)When using diff=, adding options=difall applies the differencing method among all of the six means.
%nlmeans(instore=logmod, coef=coeffs, link=glogit, options=difall, title=Program differences among all probabilities)There are now ten pairwise comparisons among all six means.
The same comparisons can be done by writing the desired expressions among the six means using f= or fdata=. In each expression, the means are referred to by the names mui, where i = 1 to 6 using the order as discussed above. For any single comparison, it is easiest to specify it in f=. For example, the following compares Pr(Style="self") with Pr(Style="team") in the afternoon Program.
%nlmeans(instore=logmod, coef=coeffs, link=glogit, f=mu1-mu3, flabel=Afternoon: Pr(Self)-Pr(Team), title=Style probability difference in afternoon)
Unlike with diff= or contrasts=, you can estimate more complex functions of the means, such as nonlinear functions, using f= (or fdata=). For example, the first macro call below reproduces the Program odds ratio estimate on the self vs class logit by expressing it as a function of the means. Mathematical functions can be included in the specified expression. The second call reproduces the Program parameter estimate on the Style=self logit, which is the log odds ratio.
%nlmeans(instore=logmod, coef=coeffs, link=glogit, f=(mu1/mu5)/(mu2/mu6), flabel=odds(Aft)/odds(Reg) in Self, title=Program odds ratio in Self vs Class) %nlmeans(instore=logmod, coef=coeffs, link=glogit, f=log((mu1/mu5)/(mu2/mu6)), flabel=log[odds(Aft)/odds(Reg)] in Self, title=Program log odds ratio in Self vs Class)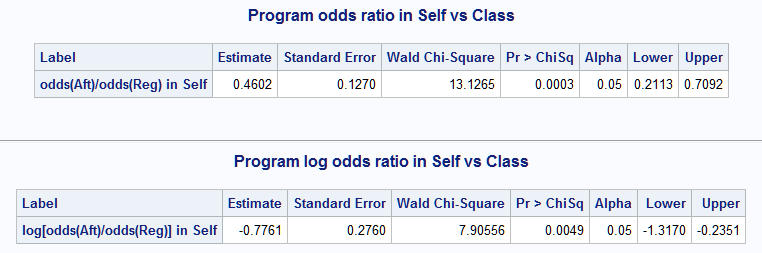
When you have multiple functions of means to estimate, they can all be estimated with a single macro call by using fdata= to specify a data set containing the function expressions. Since there is only one LSMEANS statement generating only one set of estimates in this example, the required SET variable equals 1 in each observation. The function expressions are in a variable using required name, F. Though not required, labels for the functions are provided in the LABEL variable.
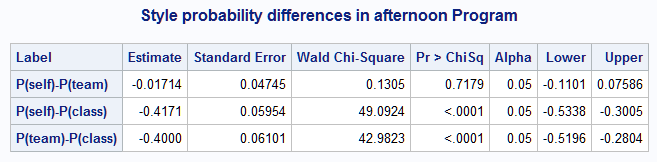
data fd; set=1; length label f $32767; infile datalines delimiter=','; input label f; datalines; P(self)-P(team), mu1-mu3 P(self)-P(class), mu1-mu5 P(team)-P(class), mu3-mu5 ; %nlmeans(instore=logmod, coef=coeffs, link=glogit, fdata=fd, title=Style probability differences in afternoon Program)The results are a subset of those shown above from using options=difall.
- EXAMPLE 3: Multiple estimate sets and options=joint
-
The following statements fit a binary logistic model to the neuralgia data in the example titled "Logistic Modeling with Categorical Predictors" in the PROC LOGISTIC documentation with data on three treatments in each of two genders (Sex). The LSMEANS and ESTIMATE statements produce a total of three estimate sets. The equivalent could be done with a single LSMEANS statement specifying both Treatment and Sex, which would produce two estimate sets, but multiple statements are used to illustrate working with multiple estimate sets.
proc logistic data=Neuralgia; class Treatment Sex / param=glm; model Pain=Treatment Sex; estimate 'F' intercept 1 Sex 1 0, 'M' intercept 1 Sex 0 1 / ilink e; lsmeans Treatment / ilink e; ods output coef=c; store clog; run;Notice that the order of the tables presented by the LSMEANS and ESTIMATE statements is not necessarily the same as the order of the statements you specify in the procedure step. The LSMEANS results are the first estimate set and the results from the ESTIMATE statements are estimate sets 2 and 3. The displayed order matches the order in the coef= data set that saves the results. This is the order to be aware of when using f= with fset= or contrasts=.

The following macro call with the default diff=all provides the pairwise comparisons among the three treatments and the two sexes.
%nlmeans(instore=clog, coef=c, link=logit, title=Treatment and Sex differences)

Because the Treatment comparisons are in estimate set 1, the following macro call using f= and fset= compares the A and P treatments.
%nlmeans(instore=clog, coef=c, link=logit, f=mu1-mu3, fset=1, flabel=Pr(Trt A)-Pr(Trt P), title=Treatment A-P difference)
To produce comparisons among all five means (three Treatment means and two Sex means), options=joint is used. This option combines the three estimate sets into a single set so that all pairwise comparisons can be made by the default diff=all.
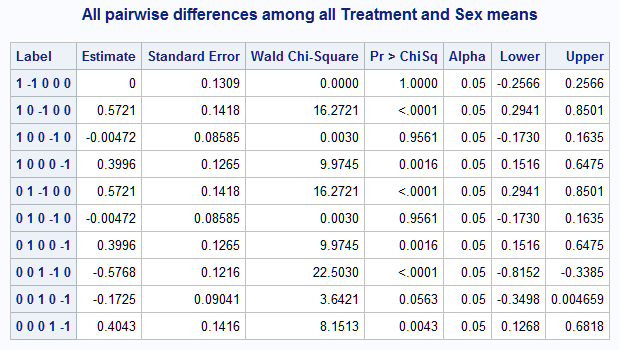
%nlmeans(instore=clog, coef=c, link=logit, options=joint, title=All pairwise differences among all Treatment and Sex means)Again, for purposes of interpreting the Label column, the five means are in the order displayed in the PROC LOGISTIC results. So, the first row showing a difference of zero compares the first two means, A and B, which both equal 0.7861 as shown above.
With all five means available, you can test a more complex hypothesis such as whether the effect of changing from Treatment P to Treatment A is the same as the Sex difference.
%nlmeans(instore=clog, coef=c, link=logit, options=joint, f=(mu1-mu3)-(mu4-mu5), flabel=Trt A-Trt P vs Female-Male, title=Difference in difference of Sex vs Treatment)
- EXAMPLE 4: BY group processing, domain analysis, analysis of imputed data, and using where=
The NLMEANS macro cannot process results from a modeling procedure that uses a BY or DOMAIN statement. However, the RunBY macro (SAS Note 66249) can be used to run the NLMEANS macro on BY groups or domains in the saved results. To process a single BY group, where= can be used. The capabilities shown below require version 1.4 or later of the NLMEANS macro, version 1.9 or later of the NLEST macro (SAS Note 58775), and version 1.1 or later of the RunBY macro.
The following uses the insurance data that appears in the example titled "Poisson Regression" in the Getting Started section of the GENMOD documentation. The differences in age rates are to be estimated by car size using separate models fit to the data for each car size. These statements fit and save the models using the STORE statement. The rates for the AGE levels in each BY group (CAR) are estimated by the LSMEANS statement in the PLM procedure. The coefficients defining the LS-means are displayed by the E option and are saved by the ODS OUTPUT statement.
proc sort data=data.insure out=insure; by car; run; proc genmod data=insure; by car; class age; model c=age / dist=poisson offset=ln; store out=insmodel; run; proc plm restore=insmodel; lsmeans age / e ilink; ods output coef=coeffs; run;Using where=
The following NLMEANS macro call specifies a condition in where= to select the large car model and estimate the difference in age rates in large cars.
%nlmeans(instore=insmodel, coef=coeffs, link=log, where=car='large', title=Difference of age rates for large cars)BY processing
The next statements process all of the BY groups using the RunBY macro. The NLMEANS macro call is placed in the CODE macro and the condition in where= is changed to use the special macro variables, _BYx and _LVLx. Since the BY groups are defined by the levels of the CAR variable in the INSURE data set, data=insure and by=car are specified in the RunBY macro call. The BYlabel macro variable is specified in title= in NLMEANS to label the displayed results with the BY group definition.
%macro code(); %nlmeans(instore=insmodel, coef=coeffs, link=log, where=&_BY1=&_LVL1, title=Difference of Age Rates &BYlabel) %mend; %RunBY(data=insure, by=car)Domain processing
Domain analysis from the survey analysis procedures is similar to BY processing in that multiple models are fit to the domains identified in the DOMAIN statement. The following uses the data in the example titled "Domain Analysis" in the SURVEYREG documentation. Dichotomized versions of the body weight and age variables, BW2 and AGEGR, are created using the RANK procedure. The SURVEYLOGISTIC procedure then estimates a logistic model in each of the two domains identified by the two levels of the CANCER variable. The fitted models are saved using the STORE statement.
It is of interest to estimate the probability of low birthweight (BW2=0) in each age group and to estimate the relative risk (ratio) of these probabilities in each of the cancer domains. The probabilities are estimated by the ILINK option in the LSMEANS statement. It is necessary to specify the LSMEANS statement in the PLM procedure rather than directly in the survey analysis procedure in order to successfully apply the where= condition. The coefficients defining the LS-means are displayed by the E option and are saved by the ODS OUTPUT statement.
proc rank data=cancer groups=2 out=c2; var bodyweight age; ranks bw2 agegr; run; proc surveylogistic data=c2; class agegr/param=glm; strata strata; cluster psu; weight ObservationWt; model bw2(event="0") = agegr; domain cancer; store out=logdom; run; proc plm restore=logdom; lsmeans agegr / e ilink; ods output coef=c; run;The following NLMEANS macro call estimates the relative risk of the age probabilities in the cancer (CANCER=1) domain. The cancer domain is selected by the where= condition. Specifying options=ratio requests computation of the ratio of estimated means from the LSMEANS statement, and null=1 tests the null hypothesis that the relative risk equals 1.
%nlmeans(instore=logdom, coef=c, where=cancer=1, link=logit, options=ratio, null=1, title=Relative Risk in cancer domain)The relative risk can be computed for both domains by using the RunBY macro in the same way as for BY processing above.
%macro code(); %nlmeans(instore=logdom, coef=c, where=&_BY1=&_LVL1, link=logit, options=ratio, null=1, title=Relative Risk for &BYlabel) %mend; %RunBY(data=c2, by=cancer)Analysis of imputed data
The analysis of multiply imputed data also involves BY processing to run the intended analysis procedure for each imputation data set. So, the use of the NLMEANS macro follows a similar procedure as above to provide the desired estimates for each imputation. The estimates from the NLMEANS macro can then be combined using the MIANALYZE procedure.
Suppose that the original data containing missing values is multiply imputed using the MI procedure, resulting in a data set, IMPUT, containing multiple imputations of the original data. The blocks of observations containing the imputations are indexed by the variable, _IMPUTATION_. Further suppose that the intended analysis on the original data involves fitting a log-linked negative binomial model to the repeated measurements on the count response, and the desire is to estimate the difference in mean count between levels of a categorical predictor. Then, given the IMPUT data set of the original data, the following statements conduct the analysis on each imputation data set, saves the fitting model in item store NB, and saves the coefficients on the model parameters defining the LS-means for categorical predictor of interest, A, in data set C. Predictor A might have two or more distinct levels. The ODS EXCLUDE and ODS SELECT options are used to suppress the displayed results from the multiple analyses.
ods exclude all; proc genmod data=imput; by _imputation_; class a subj; model c = x a / dist=negbin link=log; lsmeans a / ilink e; repeated subject=subj; store nb; ods output coef=c; run; ods select all;Using the above approach for BY processing, the NLMEANS macro can now be used inside the RunBY macro to estimate the difference in mean counts for each imputation data set. In the RunBY macro, the _BY1 macro variable in this case is the _IMPUTATION_ variable provided by PROC MI. Its values are 1, 2, 3, ... and are represented by the _LVL1 macro variable. The NONAMES and NOPRINT options in the NLMEANS macro are used to suppress all displayed results from the multiple runs of the NLMEANS macro. The NLMEANS macro automatically saves the results from each run in data set EST. Since this data set does not contain the _IMPUTATION variable and value for each run, it is added in the DATA EST step. The APPEND procedure is used to accumulate the mean difference results in data set ALLDIFF.
%macro code; %nlmeans(instore=nb, coef=c, link=log, where=&_BY1=&_LVL1, options=nonames noprint, title=rate diffs) data est; set est; _imputation_=&_LVL1; run; proc append base=alldiff data=est; run; %mend; %runby(data=imput, by=_imputation_)Finally, the NLMEANS results in data set ALLDIFF from the multiple imputations can be combined into a single estimate for each mean difference using the MIANALYZE procedure. The mean difference estimates are in the variable Estimate and their standard errors are in the variable StandardError. The distinct (and possibly multiple) mean difference estimates from each NLMEANS analysis are identified in the Label variable.
proc sort data=alldiff; by Label; run; proc mianalyze data=alldiff; by Label; modeleffects Estimate; stderr StandardError; run;
The NLMEANS macro requires the NLEST macro which is available using the Downloads tab in the NLEST macro documentation. Right-click the link below and select Save to save the NLMEANS macro definition to a file. It is recommended that you name the file nlmeans.sas.
| Type: | Sample |
| Topic: | Analytics ==> Regression SAS Reference ==> Macro |
| Date Modified: | 2025-10-06 09:55:40 |
| Date Created: | 2018-05-23 16:41:36 |
Operating System and Release Information
| Product Family | Product | Host | SAS Release | |
| Starting | Ending | |||
| SAS System | SAS/STAT | Microsoft Windows 8 Enterprise 32-bit | ||
| z/OS | ||||
| z/OS 64-bit | ||||
| OpenVMS VAX | ||||
| Microsoft® Windows® for 64-Bit Itanium-based Systems | ||||
| Microsoft Windows Server 2003 Datacenter 64-bit Edition | ||||
| Microsoft Windows Server 2003 Enterprise 64-bit Edition | ||||
| Microsoft Windows XP 64-bit Edition | ||||
| Microsoft® Windows® for x64 | ||||
| OS/2 | ||||
| Microsoft Windows 8 Enterprise x64 | ||||
| Microsoft Windows 8 Pro 32-bit | ||||
| Microsoft Windows 8 Pro x64 | ||||
| Microsoft Windows 8.1 Enterprise 32-bit | ||||
| Microsoft Windows 8.1 Enterprise x64 | ||||
| Microsoft Windows 8.1 Pro 32-bit | ||||
| Microsoft Windows 8.1 Pro x64 | ||||
| Microsoft Windows 10 | ||||
| Microsoft Windows 95/98 | ||||
| Microsoft Windows 2000 Advanced Server | ||||
| Microsoft Windows 2000 Datacenter Server | ||||
| Microsoft Windows 2000 Server | ||||
| Microsoft Windows 2000 Professional | ||||
| Microsoft Windows NT Workstation | ||||
| Microsoft Windows Server 2003 Datacenter Edition | ||||
| Microsoft Windows Server 2003 Enterprise Edition | ||||
| Microsoft Windows Server 2003 Standard Edition | ||||
| Microsoft Windows Server 2003 for x64 | ||||
| Microsoft Windows Server 2008 | ||||
| Microsoft Windows Server 2008 R2 | ||||
| Microsoft Windows Server 2008 for x64 | ||||
| Microsoft Windows Server 2012 Datacenter | ||||
| Microsoft Windows Server 2012 R2 Datacenter | ||||
| Microsoft Windows Server 2012 R2 Std | ||||
| Microsoft Windows Server 2012 Std | ||||
| Microsoft Windows Server 2016 | ||||
| Microsoft Windows XP Professional | ||||
| Windows 7 Enterprise 32 bit | ||||
| Windows 7 Enterprise x64 | ||||
| Windows 7 Home Premium 32 bit | ||||
| Windows 7 Home Premium x64 | ||||
| Windows 7 Professional 32 bit | ||||
| Windows 7 Professional x64 | ||||
| Windows 7 Ultimate 32 bit | ||||
| Windows 7 Ultimate x64 | ||||
| Windows Millennium Edition (Me) | ||||
| Windows Vista | ||||
| Windows Vista for x64 | ||||
| 64-bit Enabled AIX | ||||
| 64-bit Enabled HP-UX | ||||
| 64-bit Enabled Solaris | ||||
| ABI+ for Intel Architecture | ||||
| AIX | ||||
| HP-UX | ||||
| HP-UX IPF | ||||
| IRIX | ||||
| Linux | ||||
| Linux for x64 | ||||
| Linux on Itanium | ||||
| OpenVMS Alpha | ||||
| OpenVMS on HP Integrity | ||||
| Solaris | ||||
| Solaris for x64 | ||||
| Tru64 UNIX | ||||