Usage Note 24177: Comparing parameters (slopes) from a model fit to two or more groups
 |  |  |
Suppose that a model is fit to a set of independent groups using the same predictors and you want to compare the parameters of these models across groups. Comparison of group parameters can be done the same way regardless of the model type (ordinary regression, logistic regression, Poisson regression, etc.) and involves specifying a single model that simultaneously estimates the intercepts and slopes for all groups. When a single model estimates all the parameters of interest, you can perform tests comparing them. This is also known as testing for the heterogeneity (or homogeneity) of slopes. For example, these statements estimate a model that contains separate intercepts for each group (the GROUP effect), a single common slope on X, and a set of parameters that represent the deviations of the groups' slopes from the common slope (the X*GROUP effect):
class group;
model y = group x x*group;
run;
For procedures such as LOGISTIC and GENMOD, which allow different coding methods for CLASS variables, it is important to use GLM parameterization (also called indicator or dummy coding) of the group variable. This is done with the PARAM=GLM option in the CLASS statement. Note that for ordinary regression models fit using PROC REG, which does not have a CLASS statement, the single multi-group model can be fit in PROC GLM, which does have a CLASS statement.
To simplify interpretation, you can include the NOINT option in the MODEL statement to suppress the overall intercept. Without an overall intercept, the GROUP parameters are the intercepts for each group. With an overall intercept, the GROUP parameters are deviations between the GROUP intercepts and the overall intercept.
When there are more than two groups, the X*GROUP effect will have multiple parameters, but most procedures can provide a single Type 3 test of the effect either by default or by including an option such as TYPE3. If the test for the X*GROUP effect in the above model is significant, then this indicates that the deviations of the groups' slopes from the common slope are not all zero, meaning that some slopes are unequal. Then here is the final model with separate intercepts and slopes for the groups:
class group;
model y = group x*group / noint;
run;
If the X*GROUP effect is not significant and you accept that the groups have a common slope, then this is the parallel lines model (separate intercepts, common slope):
class group;
model y = group x / noint;
run;
This method can be applied to models that involve multiple predictors. For example, these statements test for equal slopes on both the X1 and X2 variables:
class group;
model y = group x1 x1*group x2 x2*group;
run;
Comparing Group Slopes in a Normal Response Model
See the Parameter interpretation in an ANCOVA model section of SAS Note 38384 for an example comparing the slopes of different drugs on a normally distributed response.
Comparing Group Slopes in a Poisson Model for Rates
The following statements create a data set in which the number of events (COUNT) is observed at each level of X. The amount of exposure at the levels of X are not equal, so the amount of exposure is also recorded at each level of X. The rate at each level of X is computed as the count divided by the exposure. The log of this rate is also computed.
Suppose that observations with X less than 7 are considered as one group (GROUP=1) while observations with X equal to 7 or greater are considered as a second group (GROUP=0). It is of interest to see whether the rates from these groups exhibit the same slope on X.
Note that the log of the exposure is computed for use as an offset in a Poisson model. The handling of differing exposures through use of an offset is discussed and illustrated in SAS Note 24188:
data a;
input x count exposure;
group=(x<7);
rate=count/exposure;
lograte=log(rate);
off = log(exposure);
datalines;
1 40 51000
2 27 50000
3 19 48000
4 23 47500
5 14 46500
6 12 46000
7 19 50000
8 8 47500
9 12 49000
10 8 51000
11 7 53500
;
These statements produce a plot of the observed rates across the levels of X with the groups identified:
proc sgplot;
series y=rate x=x / group=group;
run;
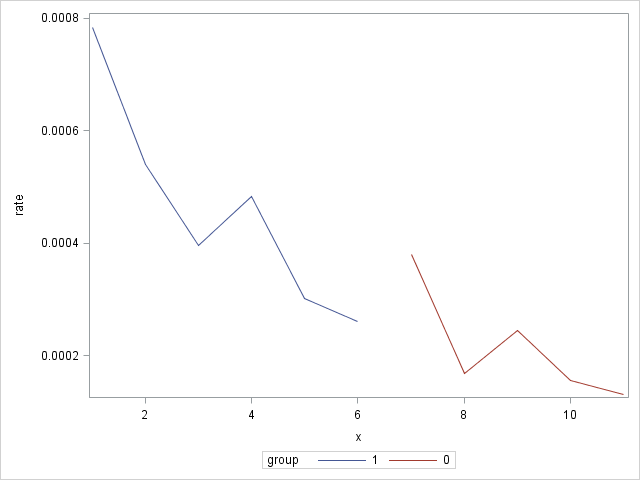 |
As discussed above, a single Poisson model that allows the groups to have separate intercepts and separate slopes is fit to the data using PROC GENMOD. The offset is included so that the rates can be modeled. Two EFFECTPLOT statements are included to plot the group models. The first EFFECTPLOT statement produces a plot on the log rate scale (LINK option). On this scale, the group models in the log-linked Poisson model are straight lines and can be compared without reference to where on X the comparison is made. The second EFFECTPLOT statement plots the models on the rate scale (ILINK option). On this scale, the group models are curves and their slopes change depending on the location on X. The MOFF option allows plotting of rates or log rates rather than counts or log counts. The OBS option displays the observed rates or log rates as points on the plots. Note that the same statements below can be used for any number of groups:
proc genmod data=a;
class group;
model count = group x*group / dist=poisson noint offset=off;
effectplot slicefit(x=x sliceby=group) / moff link obs;
effectplot slicefit(x=x sliceby=group) / moff ilink obs;
run;
The plot of the log rates shows that the slopes of the group lines are very similar, which suggests that a simpler model with a single, common slope might be sufficient. That will be tested next.
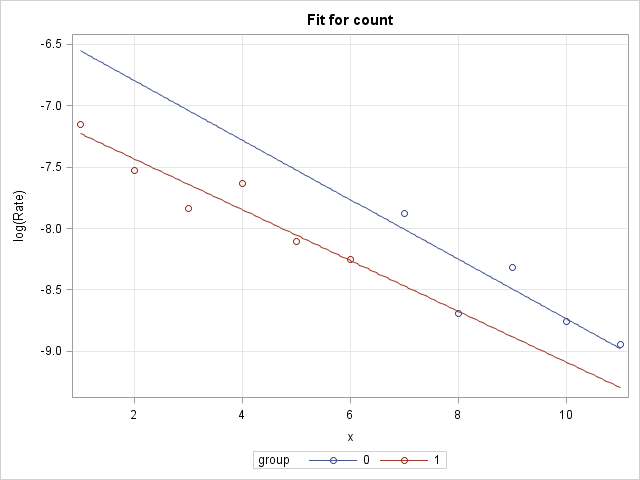 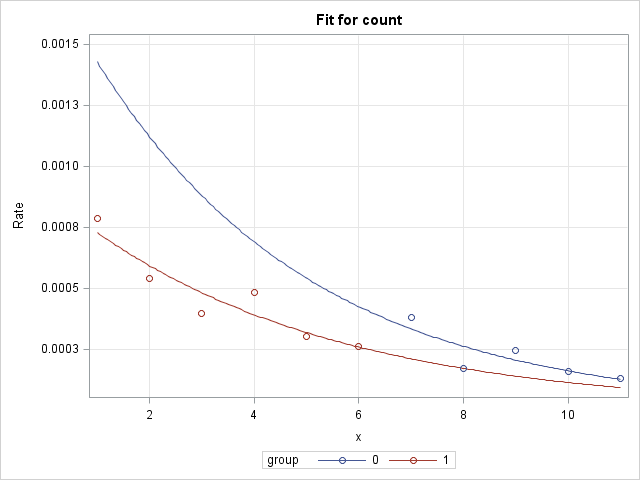 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Compare Slopes on the Log Rate Scale
These statements add the common slope X to the model. The X*GROUP effect contains the deviations of the group slopes from the common slope. If these are all zero, then there is only a single slope. So, a test of the X*GROUP effect is a test of the null hypothesis that all group slopes are the same on the log rate scale:
proc genmod data=a;
class group;
model count = group x x*group / dist=poisson noint offset=off;
run;
The nonsignificance of the X*GROUP test (p=0.7487) indicates no evidence for the group slopes differing from the common slope:
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
If you choose to accept the null hypothesis of a common slope, then these statements fit the common slope model by dropping the X*GROUP effect. The same EFFECTPLOT statements are used to plot the log rates and rates against X:
proc genmod data=a;
class group;
model count = group x / dist=poisson noint offset=off;
effectplot slicefit(x=x sliceby=group) / moff link obs;
effectplot slicefit(x=x sliceby=group) / moff ilink obs;
run;
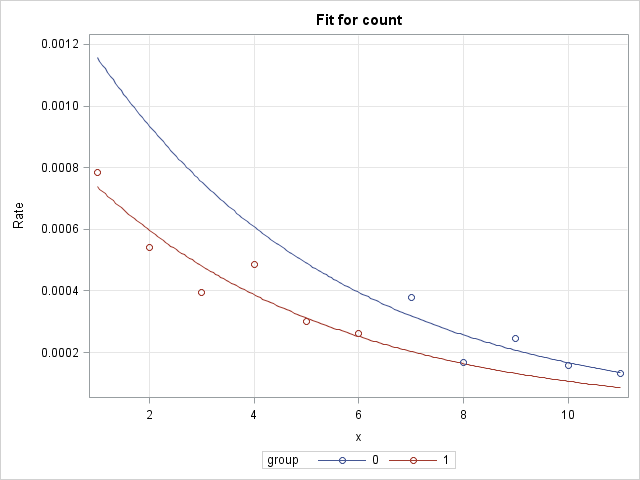
The group slopes are exactly parallel under this model, which is apparent in the plot of the log rates:
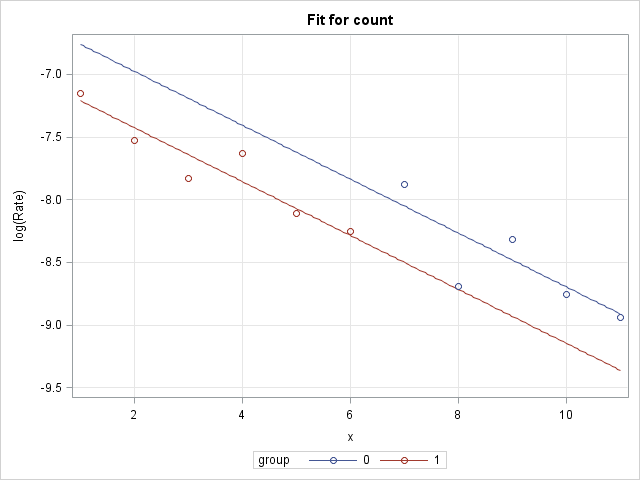  |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Compare Slopes on the Rate Scale
As shown in the rate scale plots above, the group associations between the rate and X are curved. As a result, the slope changes at each point on X and therefore a comparison of the slopes depends on the location on X where the comparison is made. The slope at a specific point on X is the slope of a line drawn tangent to the curve at that point. This is called the marginal effect of X at that point and can be estimated using the Margins macro (SAS Note 63038). Using marginal effects to compare group slopes is further discussed and illustrated in SAS Note 70756.
The following estimates and compares the group slopes at X=2, 6, and 10. Note that you need to specify your model in the Margins macro, which then refits that model using PROC GENMOD. This is done in the macro options data= through offset=. By default, the macro results include the results from PROC GENMOD, which allows you to verify that the desired model was fit. The estimation of marginal effects (slopes) on X is requested by effect=x. By including margins=group, the macro computes the marginal effects for each group. To specify the points at which the marginal effects are computed, atwhere=(x in (2,6,10)) is specified. To request that the marginal effects be compared, diff=all is specified. Since the model includes an offset in order to model the rate and estimates of the slopes on the rates are desired, the RATE option is specified. By default, the macro will compute the requested differences as Group 0 - Group 1. To reverse this differencing order, the REVERSE option is specified. Finally, confidence limits for the marginal effects and differences are requested with the CL option. For details about all available options as well as additional examples, see the Margins macro documentation (SAS Note 63038).
%margins(data=a, class=group, response=count,
model=group x*group, dist=poisson, modelopts=noint, offset=off,
margins=group, effect=x,
at=x, atwhere=(x in (2,6,10)),
diff=all, options=rate reverse cl)
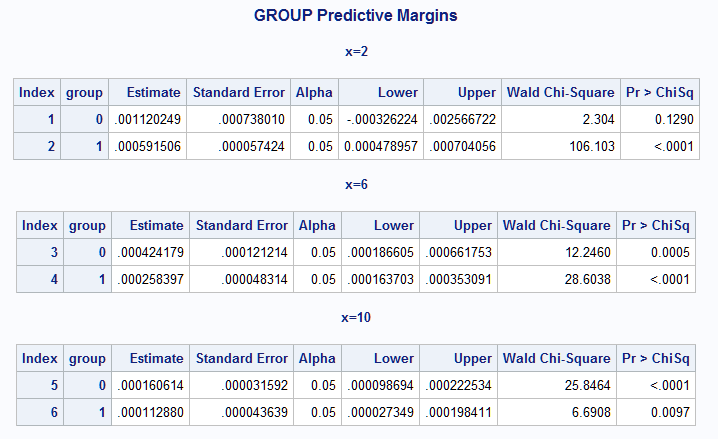
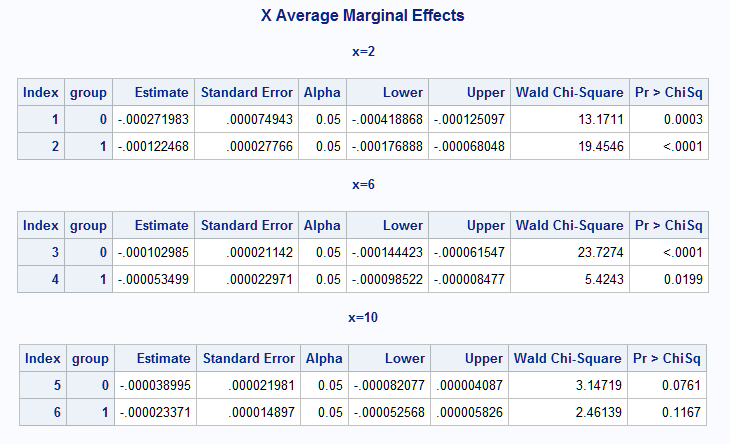
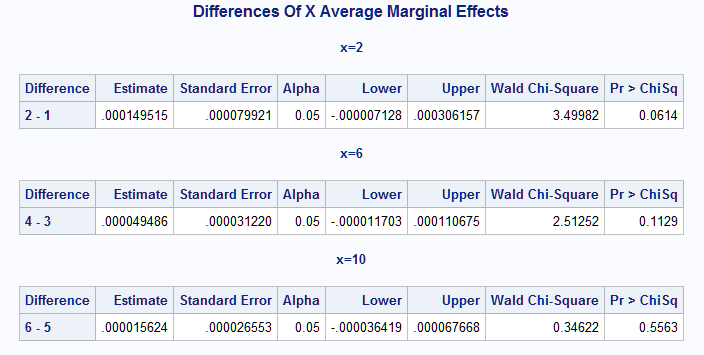
The results from the macro include, as noted above, the PROC GENMOD output showing the refit of the model (not shown). The estimated group slopes at the selected points on X are shown in the X Average Marginal Effects table. The differences (Group 1 - Group 0) of the slopes at each point are in the Differences Of X Average Marginal Effects table.
Note that all slopes are negative but the slope on group 0 is more strongly negative than on group 1 as can be seen in the fitted rate plot above. The difference in the slopes can be seen to diminish at increasing values of X and this is reflected in the diminishing difference in the marginal effects. Note that the slope difference approaches significance only at X=2 (p=0.0614)
The previous tables produced by the macro, GROUP Predictive Margins and Differences Of GROUP Margins, present the estimated rates in each group at each of the selected values of X as well as their differences:
    |
Operating System and Release Information
| Product Family | Product | System | SAS Release | |
| Reported | Fixed* | |||
| SAS System | SAS/STAT | All | n/a | |
| Type: | Usage Note |
| Priority: | low |
| Topic: | Analytics ==> Longitudinal Analysis SAS Reference ==> Procedures ==> GLM SAS Reference ==> Procedures ==> GENMOD SAS Reference ==> Procedures ==> LIFEREG SAS Reference ==> Procedures ==> MIXED SAS Reference ==> Procedures ==> LOGISTIC SAS Reference ==> Procedures ==> PROBIT Analytics ==> Regression SAS Reference ==> Procedures ==> ROBUSTREG Analytics ==> Multivariate Analysis SAS Reference ==> Procedures ==> REG SAS Reference ==> Procedures ==> SURVEYLOGISTIC SAS Reference ==> Procedures ==> SURVEYREG Analytics ==> Categorical Data Analysis Analytics ==> Survey Sampling and Analysis SAS Reference ==> Macro |
| Date Modified: | 2024-04-29 09:21:37 |
| Date Created: | 2004-10-04 11:29:37 |