The SPP Procedure
-
Overview

- Getting Started
-
Syntax

-
Details
 Testing for Complete Spatial RandomnessExploring Interpoint InteractionDistance Functions for Multitype Point PatternsBorder Edge Correction for Distance FunctionsConfidence Intervals for Summary StatisticsRipley-Rasson Window EstimatorCovariate Dependence TestsNonparametric Intensity EstimationInhomogeneous Poisson Process Model FittingNegative Binomial ModelingOutput Data SetsDisplayed OutputODS Table NamesODS Graphics
Testing for Complete Spatial RandomnessExploring Interpoint InteractionDistance Functions for Multitype Point PatternsBorder Edge Correction for Distance FunctionsConfidence Intervals for Summary StatisticsRipley-Rasson Window EstimatorCovariate Dependence TestsNonparametric Intensity EstimationInhomogeneous Poisson Process Model FittingNegative Binomial ModelingOutput Data SetsDisplayed OutputODS Table NamesODS Graphics -
Examples

- References
Inhomogeneous Poisson Process Model Fitting
Subsections:
An inhomogeneous Poisson process that has intensity function 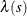 is a point process in which the number of points that fall in a spatial region W,
is a point process in which the number of points that fall in a spatial region W, 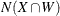 has the following expectation:
has the following expectation:
![\[ \mathbb {E}[N(X\cap W)] = \int _ W \lambda (s) ds \]](images/statug_spp0165.png)
Also, the 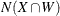 points are independent and identically distributed for disjoint subsets W with a probability density of
points are independent and identically distributed for disjoint subsets W with a probability density of
![\[ f(s) = \frac{\lambda (s)}{\int _ W \lambda (s)ds} \]](images/statug_spp0166.png)
.