The SPP Procedure

Likelihood Methods for Model Fitting

The intensity function 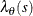$\lambda _\theta (s)$ is assumed to be log linear in the parameters 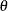$\theta $. So

\[ \log \lambda _\theta (s) = \theta \cdot Z(s) \]

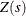where $Z(s)$ is a real-valued or vector-valued function of location s. 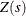$Z(s)$ can include a polynomial function of coordinate variables or a spatial covariate. The log likelihood for the parameters 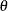$\theta $ is given by

\[ \log L(\theta ;x) = \sum _{i=1}^{n} \log \lambda _\theta (x_ i) - \int _ W \lambda _\theta (s)ds \]

The integral in the expression for the log likelihood can be approximated using quadrature as

\[ \int _ W \lambda _\theta (s;x)ds \approx \sum _{j=1}^{m}\lambda _\theta (s_ j;x)w_ j \]

for some quadrature weights 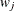$w_ j$. Hence, the log likelihood can be rewritten as follows:

\[ \log L(\theta ;x) \approx \sum _{i=1}^{n(x)}\log \lambda _\theta (x_ i;x) - \sum _{j=1}^{m}\lambda _\theta (s_ j;x)w_ j \]

Based on the observation by Berman and Turner (1992) and Baddeley and Turner (2000), the log likelihood can be approximated as

\[ \log L(\theta ;x) \approx \sum _{j=1}^{m}(y_ j\log \lambda _ j-\lambda _ j)w_ j \]

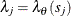where $\lambda _ j = \lambda _\theta (s_ j)$. If the list of points 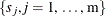$\{ s_ j\text {,}j=\text {1, \ldots , m}\} $ also includes the collection of data points 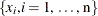$\{ x_ i\text {,}i=\text {1, \ldots , n}\} $, then 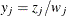$y_ j= z_ j / w_ j$ and

\[ z_ j = \begin{cases} 1 & \text {if } s_ j \text {is a data point, } s_ j \in x \\ 0 & \text {if } s_ j \text {is a dummy point, } s_ j \not\in x \end{cases} \]

The log pseudolikelihood can be maximized using standard optimization algorithms.