The SPP Procedure

Confidence Intervals for Summary Statistics

The SPP procedure computes confidence intervals for the true value of a summary statistic such as the K, L, F, G, J, or PCF function. The window that contains the point pattern is divided into a number of blocks. By default, PROC SPP divides the window into 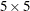$5 \times 5$ blocks. The summary statistic is calculated in each block, and the pointwise sample mean, sample variance, and sample standard deviation of these summary statistics are computed. If any edge corrections are required, they are also applied in the calculation of the individual summary statistics within each block. If the summary statistic is a function such as the K function, the estimate for a particular block B is computed by counting pairs of points in which the first point lies in B and the second point lies elsewhere  (Baddeley and Turner 2013).

The variance of the summary statistics is estimated by

\[ \hbox{var}(\tilde{K}(t)) \approx \frac{\sum _{i=1}^{m}\{ k_ i - \tilde{K}(t)\} }{\{ m(m-1)\} } \]

where m is the number of blocks, 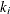$k_ i$ is the value of the summary statistic in individual blocks, and 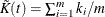$\tilde{K}(t) = \sum _{i=1}^{m}k_ i/ m$ (Diggle 2003, 52–53).