The SPP Procedure
-
Overview

- Getting Started
-
Syntax

-
Details
 Testing for Complete Spatial RandomnessExploring Interpoint InteractionDistance Functions for Multitype Point PatternsBorder Edge Correction for Distance FunctionsConfidence Intervals for Summary StatisticsRipley-Rasson Window EstimatorCovariate Dependence TestsNonparametric Intensity EstimationInhomogeneous Poisson Process Model FittingNegative Binomial ModelingOutput Data SetsDisplayed OutputODS Table NamesODS Graphics
Testing for Complete Spatial RandomnessExploring Interpoint InteractionDistance Functions for Multitype Point PatternsBorder Edge Correction for Distance FunctionsConfidence Intervals for Summary StatisticsRipley-Rasson Window EstimatorCovariate Dependence TestsNonparametric Intensity EstimationInhomogeneous Poisson Process Model FittingNegative Binomial ModelingOutput Data SetsDisplayed OutputODS Table NamesODS Graphics -
Examples

- References
Border Edge Correction for Distance Functions
To compute the edge correction factors 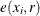 that appear in the formulas of the distance functions, the SPP procedure implements border edge correction (Illian et al.
2008; Ripley 1988; Baddeley 2007). Border edge correction is necessary because the data are given for a bounded observation window W, but the pattern itself is assumed to extend beyond the observation window. However, because you can observe only what is
within the window, a disc
that appear in the formulas of the distance functions, the SPP procedure implements border edge correction (Illian et al.
2008; Ripley 1988; Baddeley 2007). Border edge correction is necessary because the data are given for a bounded observation window W, but the pattern itself is assumed to extend beyond the observation window. However, because you can observe only what is
within the window, a disc 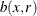 of radius r around a point x that lies close to the boundary of W might extend outside W. Because the original process X is not observed outside W, the number of points of X in
of radius r around a point x that lies close to the boundary of W might extend outside W. Because the original process X is not observed outside W, the number of points of X in 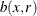 is not observable (Baddeley 2007). Ignoring the fact that the observable quantity
is not observable (Baddeley 2007). Ignoring the fact that the observable quantity 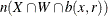 is less than or equal to
is less than or equal to 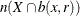 leads to a bias that is caused by edge effects. The border edge corrector is a simple strategy to eliminate the bias that
is caused by edge effects. Under the border method, the window W is replaced by a reduced window,
leads to a bias that is caused by edge effects. The border edge corrector is a simple strategy to eliminate the bias that
is caused by edge effects. Under the border method, the window W is replaced by a reduced window,
![\[ W_{\circleddash r} = W \circleddash b(0,r) = \{ x \in W: ||x - \partial W||\geq r \} \]](images/statug_spp0110.png)
where 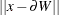 denotes the minimum distance from X to a point on the boundary. The reduced window contains all the points in W that are at least r units away from the boundary
denotes the minimum distance from X to a point on the boundary. The reduced window contains all the points in W that are at least r units away from the boundary 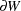 .
.
Based on the preceding definition, the border edge corrected F, K, and G functions are
![\[ \hat{F}(r) = \frac{1}{\lambda |W_{\circleddash r}|}\sum _{g_ j\in W_{\circleddash r}} \Strong{1}\{ d(g_ j,x) \leq r\} \]](images/statug_spp0112.png)
![\[ \hat{K}(r) = \frac{\sum _{i=1}^{n} \sum _{j\ne i} \Strong{1}\{ ||x_ i - x_ j|| \leq r\} }{\hat{\beta } n(x \cap W_{\circleddash r})} \]](images/statug_spp0113.png)
![\[ \hat{G}(r) = \frac{\sum _{x_ i \in W_{\circleddash r}} \Strong{1}\{ ||x_ i - X/\ x_ i|| \leq r \} }{n(X\cap W_{\circleddash r})} \]](images/statug_spp0114.png)
![\[ \hat{G}(r) = \frac{\sum _ i \Strong{1}\{ d_ i \leq r, b_ i \geq r \} }{\sum _ i\Strong{1}\{ b_ i \geq r\} } \]](images/statug_spp0115.png)
where 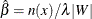 ;
; 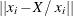 is the observed nearest-neighbor distance,
is the observed nearest-neighbor distance, 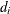 , for the ith point
, for the ith point 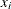 ; and
; and 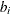 is the distance from
is the distance from 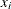 to the boundary
to the boundary 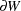 . For more information about these border-edge-corrected functions, see Baddeley (2007).
. For more information about these border-edge-corrected functions, see Baddeley (2007).