The SPP Procedure
-
Overview

- Getting Started
-
Syntax

-
Details
 Testing for Complete Spatial RandomnessExploring Interpoint InteractionDistance Functions for Multitype Point PatternsBorder Edge Correction for Distance FunctionsConfidence Intervals for Summary StatisticsRipley-Rasson Window EstimatorCovariate Dependence TestsNonparametric Intensity EstimationInhomogeneous Poisson Process Model FittingNegative Binomial ModelingOutput Data SetsDisplayed OutputODS Table NamesODS Graphics
Testing for Complete Spatial RandomnessExploring Interpoint InteractionDistance Functions for Multitype Point PatternsBorder Edge Correction for Distance FunctionsConfidence Intervals for Summary StatisticsRipley-Rasson Window EstimatorCovariate Dependence TestsNonparametric Intensity EstimationInhomogeneous Poisson Process Model FittingNegative Binomial ModelingOutput Data SetsDisplayed OutputODS Table NamesODS Graphics -
Examples

- References
Distance Functions for Multitype Point Patterns
Distance functions (such as G, J, K, L, and g) can also be defined for point patterns that are "marked" with a categorical
mark variable, called a type. Usually you consider mark variables that have more than one type to define distance functions.
When distance functions are defined between two types, they are called cross-type distance functions. For any pair of types
i and j, the cross-distance functions 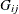 ,
, 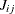 ,
, 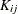 ,
, 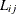 , and
, and 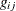 can be defined analogously to the single-type distance functions. The interpretation of cross-type distance functions is
slightly different from the interpretation of single type functions. Suppose that X is the point pattern,
can be defined analogously to the single-type distance functions. The interpretation of cross-type distance functions is
slightly different from the interpretation of single type functions. Suppose that X is the point pattern, 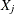 refers to the subpattern of points of type j;
refers to the subpattern of points of type j; 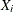 refers to the subpattern of points of type i, and
refers to the subpattern of points of type i, and 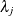 represents the intensity of the subpattern
represents the intensity of the subpattern 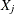 . Then the interpretation is to treat
. Then the interpretation is to treat 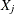 as a homogeneous Poisson process and independent of
as a homogeneous Poisson process and independent of 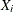 . If the computed empirical cross-type function is identical to the function that corresponds to a homogeneous Poisson process,
then
. If the computed empirical cross-type function is identical to the function that corresponds to a homogeneous Poisson process,
then 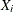 and
and 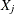 can be treated as independent of each other.
can be treated as independent of each other.
The empirical cross-G-function, 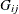 , is defined as the distribution of the distance from a point of type i in
, is defined as the distribution of the distance from a point of type i in 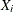 to the nearest point of type j in
to the nearest point of type j in 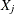 . Formally,
. Formally, 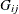 can be written as
can be written as
![\[ G_{ij}(r) = \sum _ ie(x_ i,r)\Strong{1}\{ d_{ij}\leq r\} \]](images/statug_spp0091.png)
where 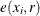 is an edge correction and
is an edge correction and 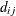 is the distance from a point of type i to the nearest point of type j. If the two subpatterns
is the distance from a point of type i to the nearest point of type j. If the two subpatterns 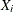 and
and 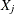 are independent of each other, then the theoretical cross-G-function is
are independent of each other, then the theoretical cross-G-function is
![\[ G_{ij}^{*}(r)= 1-\exp {(\lambda _ j \pi r^{2})} \]](images/statug_spp0093.png)
The empirical cross-type J-function, 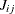 , can be defined again in terms of the
, can be defined again in terms of the 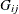 function and the empty-space F function for subpattern
function and the empty-space F function for subpattern 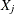 as
as
![\[ J_{ij}(r) = J_{ij}(r) = \frac{1-G_{ij}(r)}{1-F_ j(r)} \]](images/statug_spp0094.png)
where 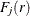 is the empty-space function for the subpattern
is the empty-space function for the subpattern 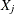 . If the two subpatterns
. If the two subpatterns 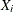 and
and 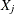 are independent of each other, then the theoretical cross-J-function is
are independent of each other, then the theoretical cross-J-function is 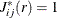 .
.
The empirical cross-type K function, 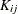 , is
, is 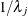 times the expected number of points of type j within a distance r of a typical point of type i. Formally,
times the expected number of points of type j within a distance r of a typical point of type i. Formally, 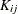 can be written as
can be written as
![\[ K_{ij}(r) = K_{ij}(r) = \frac{1}{\lambda _ j \lambda _ i |W|}\sum _ i \sum _ j \Strong{1}\{ ||x_ i-x_ j||\leq r\} e(x_ i,x_ j;r) \]](images/statug_spp0098.png)
where 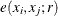 is an edge correction. If the two subpatterns
is an edge correction. If the two subpatterns 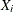 and
and 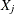 are independent of each other, then the theoretical cross-K-function is
are independent of each other, then the theoretical cross-K-function is 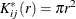 .
.
The empirical cross-type L function, 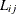 , is a transformation of
, is a transformation of 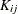 . Formally,
. Formally, 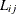 can be written as
can be written as
![\[ L_{ij}(r) = L_{ij}(r) = \sqrt {\frac{K_{ij}(r)}{2\pi r}} \]](images/statug_spp0100.png)
If the two subpatterns 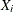 and
and 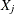 are independent of each other, then the theoretical cross-type L-function is
are independent of each other, then the theoretical cross-type L-function is 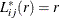 .
.
The empirical cross-type pair correlation function, 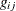 , is a kernel estimate of the form
, is a kernel estimate of the form
![\[ g_{ij}(r) = \frac{\rho (r)}{\hat{\lambda }^{2}} = \frac{1}{2\pi r \hat{\lambda }_ i \hat{\lambda }_ j}\sum _ i \sum _ j \frac{k_ h(||x_ i-x_ j||-r)}{|W \cap W_{i-j}|} \]](images/statug_spp0102.png)
Based on the definition of Stoyan and Stoyan (1994), 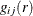 can be written as
can be written as
![\[ g_{ij}(r) = \frac{\rho (r)}{\hat{\lambda }^{2}} = \frac{1}{2\pi r \hat{\lambda }_ i \hat{\lambda }_ j}\sum _ i \sum _ j \frac{k_ h(||x_ i-x_ j||-r)}{|W_{x_ i} \cap W_{x_ j}|} \]](images/statug_spp0104.png)
A border-edge-corrected version of 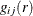 can be written as
can be written as
![\[ g_{ij}(r) = \frac{1}{2 \pi r \hat{\lambda _ j}} \frac{\sum _ i \sum _ jk_ h(||x_ i-x_ j||-r)}{\sum _ i \Strong{1}\{ b_ i \geq r\} } \]](images/statug_spp0105.png)
where 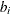 is the distance of
is the distance of 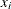 to the boundary of W, which is denoted as
to the boundary of W, which is denoted as 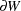 . If the two subpatterns
. If the two subpatterns 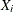 and
and 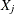 are independent of each other, then the theoretical cross-type pair correlation function is
are independent of each other, then the theoretical cross-type pair correlation function is 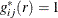 .
.