The SPP Procedure
-
Overview

- Getting Started
-
Syntax

-
Details
 Testing for Complete Spatial RandomnessExploring Interpoint InteractionDistance Functions for Multitype Point PatternsBorder Edge Correction for Distance FunctionsConfidence Intervals for Summary StatisticsRipley-Rasson Window EstimatorCovariate Dependence TestsNonparametric Intensity EstimationInhomogeneous Poisson Process Model FittingNegative Binomial ModelingOutput Data SetsDisplayed OutputODS Table NamesODS Graphics
Testing for Complete Spatial RandomnessExploring Interpoint InteractionDistance Functions for Multitype Point PatternsBorder Edge Correction for Distance FunctionsConfidence Intervals for Summary StatisticsRipley-Rasson Window EstimatorCovariate Dependence TestsNonparametric Intensity EstimationInhomogeneous Poisson Process Model FittingNegative Binomial ModelingOutput Data SetsDisplayed OutputODS Table NamesODS Graphics -
Examples

- References
Statistics Based on Second-Order Characteristics
Statistics that are based on second-order characteristics include Ripley’s K function, Besag’s L function, and the pair correlation function (also called the g function). To understand why these functions are based on second-order characteristics, see Illian et al. (2008, p. 223-243). These functions usually involve computation of pairwise distances between points.
The K function of a stationary point process is defined such that 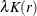 is the expected number of points within a distance of r from an arbitrary point of the process. The empirical K function
of a set of points is the weighted and renormalized empirical distribution function of the set of pairwise distances between
points. The empirical K function can be written as
is the expected number of points within a distance of r from an arbitrary point of the process. The empirical K function
of a set of points is the weighted and renormalized empirical distribution function of the set of pairwise distances between
points. The empirical K function can be written as
![\[ \hat{K}(r) = \frac{1}{\hat{\lambda }^{2} |W|}\sum _ i \sum _{j\ne i} \Strong{1}\{ ||x_ i - x_ j|| \leq r\} e(x_ i,x_ j;r) \]](images/statug_spp0053.png)
where 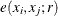 is the border edge correction that is described in the section Border Edge Correction for Distance Functions.
is the border edge correction that is described in the section Border Edge Correction for Distance Functions.
For a homogeneous Poisson process, 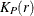 can be written as
can be written as
![\[ K_ P(r) = \pi r^{2} \]](images/statug_spp0056.png)
Exploratory analysis usually involves computing both the empirical K function, 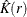 , and the K function for a Poisson process,
, and the K function for a Poisson process, 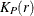 . A comparison of
. A comparison of 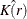 and
and 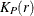 might indicate clustering or regularity depending on whether
might indicate clustering or regularity depending on whether 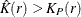 or
or 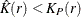 .
.
Besag’s L function is a transformation of the K function and is defined as
![\[ L(r) = \sqrt {\frac{K(r)}{\pi } } \]](images/statug_spp0061.png)
For a homogeneous Poisson process, 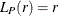 .
.
The pair correlation function, g(r), can also be expressed as a transformation of the K function:
![\[ g(r) = \frac{K'(r)}{2 \pi r} \]](images/statug_spp0063.png)
Illian et al. (2008), Stoyan (1987), and Fiksel (1988) suggest an alternative expression for 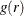 :
:
![\[ g(r) = \rho (r)/ \lambda ^{2} \]](images/statug_spp0065.png)
where 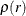 is the second-order product density function. Cressie and Collins (2001) provides an expression for
is the second-order product density function. Cressie and Collins (2001) provides an expression for 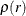 as
as
![\[ \rho (r) = \frac{\hat{\lambda ^{2}} K'(r)}{2\pi r} \]](images/statug_spp0067.png)
where 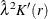 can be written as a kernel estimate,
can be written as a kernel estimate,
![\[ \hat{\lambda }^{2} K’(r) = \frac{1}{a}\sum _{i=1}^{n}\sum _{j\ne i}k_ h (||x_ i-x_ j||-r) \]](images/statug_spp0069.png)
where a is the area, 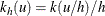 , and
, and 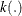 is a kernel such as the uniform kernel or the Epanechnikov kernel (Silverman 1986). PROC SPP uses the version that is based on the uniform kernel; for more information about the uniform kernel, see the section
Nonparametric Intensity Estimation. Based on the formula for the second-order product density
is a kernel such as the uniform kernel or the Epanechnikov kernel (Silverman 1986). PROC SPP uses the version that is based on the uniform kernel; for more information about the uniform kernel, see the section
Nonparametric Intensity Estimation. Based on the formula for the second-order product density 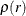 in terms of the kernel estimate, Stoyan (1987) gives an edge-corrected kernel estimate for
in terms of the kernel estimate, Stoyan (1987) gives an edge-corrected kernel estimate for 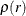 as
as
![\[ \rho (r) = \frac{1}{2\pi r }\sum _ i \sum _{j\ne i} \frac{k_ h(||x_ i - x_ j||-r)}{a(W_{x_ i} \cap W_{x_ j})} \]](images/statug_spp0072.png)
Dividing 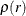 by
by 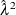 gives the pair correlation function
gives the pair correlation function 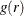 as
as
![\[ g(r) = \frac{1}{2\pi r \hat{\lambda }^{2} }\sum _ i \sum _{j\ne i} \frac{k_ h(||x_ i - x_ j||-r)}{a(W_{x_ i} \cap W_{x_ j})} \]](images/statug_spp0074.png)
where 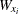 indicates the translation of the study area window W by the distance
indicates the translation of the study area window W by the distance 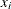 from its origin. The above expression for
from its origin. The above expression for 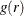 was given by Stoyan and Stoyan (1994) using the translation edge correction.
was given by Stoyan and Stoyan (1994) using the translation edge correction.
A border-edge-corrected version of 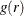 can be written as
can be written as
![\[ g(r) = \frac{1}{2\pi r \hat{\lambda }} \frac{\sum _ i \sum _{j\ne i} k_{h}(||x_ i-x_ j||-r)}{\sum _ i\Strong{1}\{ b_ i \geq r\} } \]](images/statug_spp0077.png)
where 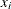 and
and 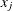 are points within the boundary at a distance greater than or equal to r; where
are points within the boundary at a distance greater than or equal to r; where 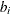 is the distance of
is the distance of 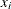 to the boundary of W,
to the boundary of W, 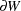 ; and where
; and where 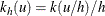 for a kernel
for a kernel 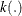 , such as the uniform kernel or the Epanechnikov kernel. For more information about the uniform kernel, see the section Nonparametric Intensity Estimation. For a homogeneous Poisson process,
, such as the uniform kernel or the Epanechnikov kernel. For more information about the uniform kernel, see the section Nonparametric Intensity Estimation. For a homogeneous Poisson process, 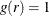 . For any point pattern, values of
. For any point pattern, values of 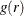 greater than 1 indicate clustering or attraction at distance r, whereas values of
greater than 1 indicate clustering or attraction at distance r, whereas values of 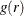 less than 1 indicate regularity.
less than 1 indicate regularity.