The SPP Procedure

Nearest-Neighbor Distance Functions

The SPP procedure implements the following nearest-neighbor distance functions:

  • empty-space F function

  • nearest-neighbor G function

  • J function

A typical test that uses any nearest-neighbor function compares the empirical distribution function with the corresponding function for a homogeneous Poisson process that has first-order intensity 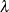$\lambda $. Usually, the first-order intensity is obtained as the number of observations per unit of area, $\hat{\lambda } = n(x) / |W|$.

The empty-space F function is defined as the empirical distribution function of the observed empty-space distances, $d(g,x)$, which is measured from a set of reference grid points g to the nearest point in the point pattern. The empty-space distance can be defined as

\[ d(g,x) = \min \{ ||g-x_ i||, \text {for }x_ i \in x\} \]

In practice, the computation of the empty-space F function also involves an edge correction. The edge-corrected empty-space F function is defined as

\[ \hat{F}(r) = \sum _ j e(g_ j,r) \Strong{1} \{ d(g_ j,x) \leq r\} \]

where $e(g_ j,r)$ is an edge correction. PROC SPP implements the border edge correction (Illian et al. 2008, p. 185–186) as described in the section Border Edge Correction for Distance Functions.

For a homogeneous Poisson process that has first-order intensity 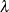$\lambda $, the F function is

\[ F_ P(r) = 1 - \exp {(-\lambda \pi r^{2})} \]

You compare the empirical and Poisson empty-space F function by using the EDF and the P-P plot in the F function summary panel plot. Values of $\hat{F}(r)> F_ P(r)$ suggest a regularly spaced pattern, and values of $\hat{F}(r)< F_ P(r)$ suggest a clustered pattern (Baddeley and Turner 2005).

The nearest-neighbor G function is the empirical distribution of the observed nearest-neighbor distance of the points within the point pattern. In practice, the G function also involves an edge correction and is defined as

\[ \hat{G}(r) = \sum _ i e(x_ i,r) \Strong{1} \{ d_ i \leq r\} \]

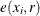where $e(x_ i,r)$ is the border edge correction (Illian et al. 2008, p. 185-186) as described in the section Border Edge Correction for Distance Functions and 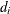$d_ i$ is the distance to the nearest neighbor for the ith point.

For a homogeneous Poisson process that has first-order intensity 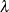$\lambda $, the G function can be defined as

\[ G_ P(r) = 1 - \exp {(-\lambda \pi r^{2})} \]

The interpretation of $\hat{G}(r)$ is opposite to the interpretation of $\hat{F}(r)$. That is, values of $\hat{G}(r) > G_ P(r)$ imply a clustered pattern, and values of $\hat{G}(r)< G_ P(r)$ suggest a regular pattern (Baddeley and Turner 2005).

The third type of nearest-neighbor distance function is the J function, which is defined as a combination of both the F and G functions (Baddeley et al. 2000). The J function is defined for all distances r such that $F(r) < 1$. The J function can be defined as

\[ J(r) = \frac{1-G(r)}{1-F(r)} \]

For a homogeneous Poisson process, $J_ P(r) = 1$. When $J(r)$ takes values greater than 1, regularity is indicated; when $J(r)$ takes values less than 1, the underlying process is more clustered than expected. As can be seen from the expression of $J(r)$, the estimate is an uncorrected estimate of the J-function and hence its computation does not require an edge correction (Baddeley et al. 2000).