The SPP Procedure

Negative Binomial Modeling

Spatial data in many applications can be overdispersed—that is, the variance of the counts of spatial events might be inflated relative to what is expected under the assumption of a Poisson model. The negative binomial modeling in PROC SPP serves as a diagnostic to assess overdispersion in your data.

The log likelihood for the negative binomial model is

\[ \log L(\theta ;x) = \sum _{i=1}^{n} \left\{ y_ i\cdot \log \left\{ \frac{\phi \cdot \lambda _ i}{w_ i}\right\} - (y_ i+\frac{w_ i}{\phi }) \cdot \log \left\{ 1 + \frac{\phi \cdot \lambda _ i}{w_ i} \right\} +\log \left\{ \frac{\Gamma (y_ i+w_ i/\phi )}{\Gamma (w_ i/\phi )\Gamma (y_ i+1)}\right\} \right\} \]

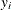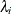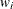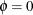where $y_ i$ is the response at a location, $\lambda _ i$ is the intensity associated with the location, $\phi $ is the negative binomial scale parameter, and $w_ i$ is the quadrature weight associated with the location. Overdispersion is indicated by the value of the scale parameter $\phi $: for $\phi = 0$, the negative binomial distribution is identical to the Poisson distribution; therefore, large values of $\phi $ indicate overdispersion.

Because the negative binomial model in PROC SPP is intended only for diagnostic purposes, the only results are the estimated parameters themselves, including $\phi $. No fitted intensity is produced, and likewise nothing that depends on the fitted intensity, such as the goodness-of-fit tests and the residual diagnostics, is produced.